Криві зв’язування (Bonding Curves) є важливим елементом криптоекономіки, оскільки вони дозволяють автоматизувати ціноутворення та забезпечити ліквідність токенів. Вони встановлюють математичну залежність між пропозицією токенів та їхньою ціною.
Ця концепція використовується у різних сферах, таких як децентралізовані фінанси (DeFi), токенізовані економіки та DAO (децентралізовані автономні організації). Криві зв’язування можуть допомогти у створенні ринків без традиційних посередників, а також у стимулюванні інвесторів через розумні механізми зміни вартості активів.
У цій статті ми розглянемо математичні моделі кривих зв’язування, їхні переваги, відмінності та застосування у смартконтрактах.
Формальна модель кривої зв’язування
Крива зв’язування визначає функціональну залежність між пропозицією токенів та їхньою ціною . Загальна математична модель виглядає так:
де — це функція ціноутворення, яка може бути лінійною, експоненціальною, логарифмічною чи іншого типу.
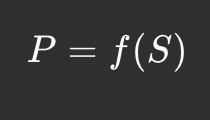
Основні типи функцій кривих зв’язування та їхні особливості
1. Лінійна крива
Приклад застосування:
Bancor використовує лінійні криві для автоматичного маркетмейкінгу, дозволяючи прогнозоване зростання ціни токенів.
DAO-ініціативи створюють токени, де кожен наступний токен коштує трохи більше за попередній.
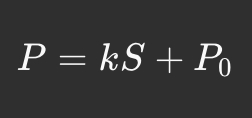
Переваги:
Простота реалізації та прогнозованість.
Лінійне зростання ціни забезпечує стабільне ціноутворення.
Недоліки:
Може призвести до великого зростання ціни при великій кількості токенів, що обмежує доступність.
Мало гнучкості в управлінні ліквідністю на різних етапах.
2. Експоненціальна крива
Приклад застосування:
NFT-платформа Zora використовує експоненційну криву для токенізації цифрового мистецтва, стимулюючи ранніх інвесторів.
Rari Capital впроваджує подібну модель у свої DeFi-пули для балансування ліквідності.
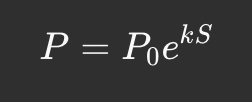
Переваги:
Стимулює ранніх інвесторів, дозволяючи їм отримати значні вигоди.
Підвищує ціну токенів з кожним новим етапом, що може залучити більший попит.
Недоліки:
Може призвести до надмірної волатильності.
Вартість може стрімко зрости, що зробить токени менш доступними для нових користувачів.
3. Логарифмічна крива
Приклад застосування:
Ampleforth (AMPL) використовує логарифмічну модель для стабілізації пропозиції токенів, коригуючи їхню вартість.
Проєкти стабільних токенів застосовують логарифмічні криві для зменшення волатильності.
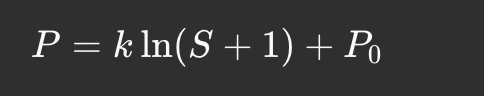
Переваги:
Забезпечує стабільність ціни навіть при значних змінах у кількості токенів.
Менше схильна до надмірної волатильності порівняно з експоненціальними кривими.
Недоліки:
Може бути менш привабливою для інвесторів, оскільки ціновий ріст сповільнюється з часом.
Може створювати бар'єри для швидкого зростання токенів на ранніх етапах.
4. Сигмоїдна (S-подібна) крива
Приклад застосування:
Gitcoin застосовує сигмоїдну модель у своїй економіці грантів для рівномірного розподілу коштів серед проєктів.
Гейміфіковані економіки, такі як Axie Infinity, використовують S-криві для обмеження пропозиції та мотивації гравців.
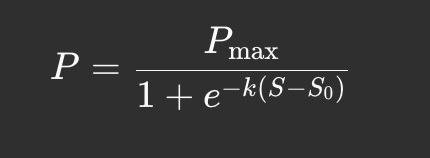
Переваги:
Забезпечує поступовий ріст ціни на початку, який сповільнюється, коли наближається до певного ліміту, що стабілізує ціну.
Ідеально підходить для довгострокових проєктів, де необхідно уникнути різких змін у вартості.
Недоліки:
Може обмежити можливості для швидкого зростання на ранніх етапах.
Кількість токенів, яка буде доступна після досягнення максимуму, може бути обмежена.
Як це допомагає невеликим токенам?
Криві зв’язування можуть бути корисними для нових та невеликих токенів завдяки:
Автоматичному ціноутворенню – ціна зростає або зменшується згідно з алгоритмом.
Прозорій ліквідності – кожен учасник може легко купити або продати токени.
Стимулюванню ранніх інвесторів – завдяки експоненціальним або комбінованим моделям.
Зниженню волатильності – використання логарифмічних або сигмоїдних кривих може стабілізувати ринок.
Застосування в смартконтрактах
Більшість DeFi-платформ використовують смартконтракти для реалізації кривих зв’язування. Вартість покупки токенів при переході від до визначається інтегралом:
Ця формула дозволяє визначити суму, необхідну для купівлі нових токенів.
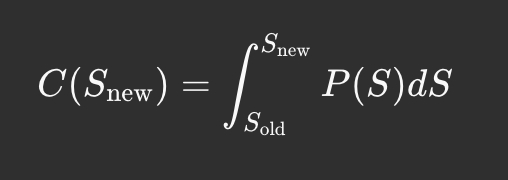
Реальні кейси використання
Uniswap (AMM-протоколи): Використовує криву постійного добутку для забезпечення ліквідності без книги ордерів.
Bancor: Впроваджує лінійну модель кривих зв’язування для створення автоматичних маркетмейкерів.
Zora: Реалізує експоненційну модель для продажу NFT, що дозволяє стрімко підвищувати їхню ціну залежно від попиту.
Gitcoin: Використовує сигмоїдну криву для рівномірного розподілу грантів.
Ampleforth (AMPL): Впроваджує логарифмічну модель для стабільного коригування пропозиції токенів.
Висновок
Криві зв’язування забезпечують автоматизоване ціноутворення та ліквідність у криптоекосистемах. Використання різних математичних моделей дозволяє адаптувати поведінку токенів до потреб проєкту.
Якщо ви хочете використати криві зв’язування у своєму проєкті — будь то DeFi-протокол, NFT-маркетплейс або DAO — звертайтеся до мене, і я допоможу підібрати найкращу модель для вашого випадку!
