Вам кортіло дізнатись, як працюють штучні нейромережі❓ Багато читали про це, але відчуваєте, що ваші знання дуже поверхневі❓ А чи знали ви про “заплутаності” в штучних нейромережах, майже як в квантовій механіці❓ Чи хотіли дізнатись, як взагалі бачить світ нейронка (спойлер: тут буде теорія кодування!!!)❓
Гайда́ тоді читати про основи нейромислення, читати та обдумувати прочитане. Не на всі питання надам відповідь, можливо питань навіть збільшиться. Але такі вже вони, основи!
І оскільки я сам ще вчусь, то спробую пояснити тему в спрощеному, але не у примітивному вигляді. Іноді простіше вчитись у не-експертів, бо в них снобізм ще не зашкалює, і вони самі пам’ятають як воно було не знати чогось. Тим не менш, дещо від читачів я очікую:
Мій читач:
- точно поважає математику, числа та формули
- було б непогано, якби був/була поверхнево знайомі з добутком матриць
- цікавиться, хоче дізнаватись щось нове про штучні нейронки або механістичну свідомість
- корисним було би знання основ програмування, але це не обов’язково
Наш кухонний стіл
Матриці — це одна з базових речей, що знаходяться під капотом штучних нейронок, або штучного “інтелекту”, як це зараз гайпово називати. Навчання нейромереж — це насправді пошук правильних, робочих матриць, які після перемножень та активацій зроблять корисний результат.
Власне, для сьогоднішнього довгочиту мені буде достатньо всього два концепти: матриці та матричний добуток.

Серед матриць я буду використовувати найменші їх види (мініматриці? мікроматриці? матрусіки чи як там зменшувально-пестливо?):
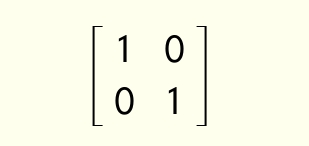
матриця 1×1
матриця 1×2
матриця 2×1
матриця 2×2
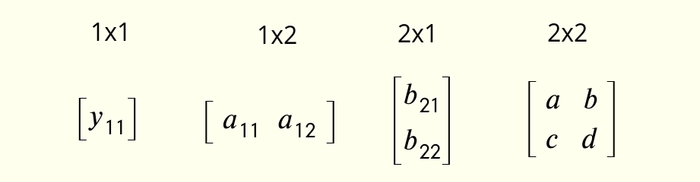
Як робиться добуток матриць (можна пропустити, якщо пам’ятаєте)
Дуже грубо кажучи, матриця — це прямокутник з чисел. Розміри цього прямокутника можуть бути будь-які. Я буду вказувати ці розміри так: M×N, де M та N — кількість рядків та кількість стовпчиків в матриці.
Отже, матриця може мати розмір 1×1. Це найпростіша матриця, яка склається з всього одного числа.
Матриця розміром 1×2 називається рядок.
Матриця розміром 2×1 називається стовпчик.
І рядок можна помножити на стовпчик по такій формулі:

Результатом множення рядка на стовпчик буде матриця 1×1. Цей частковий випадок множення матриць ще називається векторний добуток.
Ось конкретні формули для множення матриць різних розмірів:
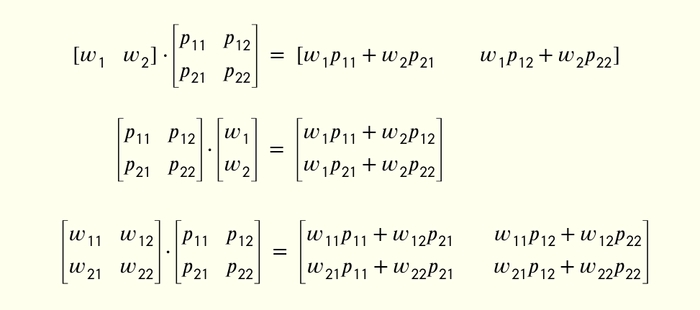
Логіка в усіх цих формулах є. Кожен елемент матриці-результату — це векторний добуток рядка з першої матриці та стовпчика з другої. Якого саме рядка та стовпичка, краще зрозуміти з цієї діаграми (тут добуток матриць 4×2 та 2×3):
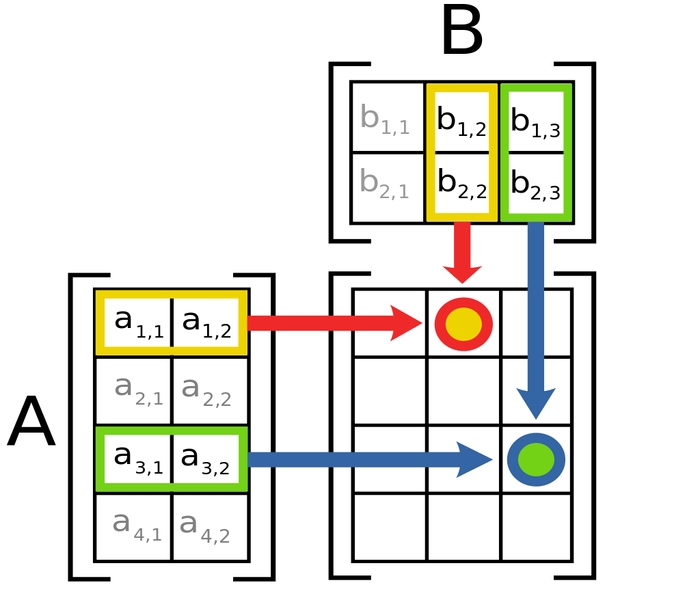
Щоб матриці можна було перемножити, кількість стовпчиків в першій матриці повинна дорівнювати кількості рядків в другій. Інакше множення не можливе.
Ну і при множенні матриці переставляти місцями не можна. Навіть якщо розміри співпадать — результат множення вийде інший.
Є винятки з цього правила, але на те вони і винятки, щоб про них поки-що помовчати.
В якості вправи спробуйте на листочку перемножити ці дві матриці та звіритись з результатом:
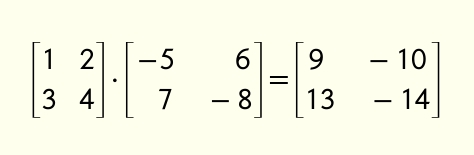
Додавання через матричний добуток
Парадоксально, але множення матриць може додавати числа!

Якщо організувати два числа a та b у матрицю 1×2, то можна отримати їх суму, якщо домножити на спеціяльну матрицю M_add.
В результаті ми отримаємо матрицю 1×1 з сумою чисел. Дивіться схемку з прикладом:

Можна сказати, що це найменша нейронка, що додає 2 числа. Ви можете в ютубі знайти відео індуса, котрий нагоро́див 6-шарову (читай, шести-матричну) нейронку ширини 12 (читай, матриці 12х12), що є дуже сильно overkill.
Не робіть як цей індус, окрім якщо це для вас цікаві досліди. Цікавість — це шлях в майбутнє! (с)
Чим це знання може вам згодитись? Звісно, ніхто в здоровому глузді не буде робити додавання чисел множенням на матрицю. Всі системи обчислень підтримують додавання. Тоді в чому сенс?
Основна ідея в тому, що це можливо. Ми ж досліджуємо нейромережі, котрі складаються з матриць. І ці нейромережі “думають”, перемножуючи ці свої матриці. Тепер ми знаємо, що нейромережа може додавати числа, бо матриці дозволяють таку операцію. І хто зна, може десь в глибині ̶д̶у̶ш̶і̶ матриці в нейронці стоять ці завітні числа 1 1 та виконують важливу місію — щось додають…
Вправа на подумати: чи можливо зробити додавання чисел через множення чисел, а не матриць? Чи можливо зробити додавання чисел через віднімання чисел?
Проте, урок буде не в цьому. Розберемось ще з відніманням.
Віднімання через матричний добуток
Схожим способом матриця може порахувати різницю чисел.

Справді, a - b = a + (-b) = a·1 + b · -1. Але треба пам’ятати, що нам може бути потрібним як a-b, так і b-a. Тому матриць віднімання насправді дві.

Виглядає не складно, правда ж? І можна помітити певну закономірність, можливість до узагальнення. Матриці додавання та віднімання мають розмір 2х1, і складаються з 1 та -1. А що станеться, якщо замість 1 та -1 будуть інші числа?
Це вже буде лінійна комбінація чисел, якщо говорити математичною мовою. І це наступна тема для вивчення.
Матриці лінійної комбінації
Для лінійних комбінацій дозволено додавання, віднімання та множення вхідної змінної на константу (конкретне число). Ось два приклади лінійних комбінацій a та b:
2a + 3b
b - 5a
Чому вони називаються “лінійні” — це окрема тема. Я не буду тут це пояснювати, розкрию ширше в майбутньому довгочиті про біаси.
Для обидвох можна побудувати відповідні матриці обчислення:
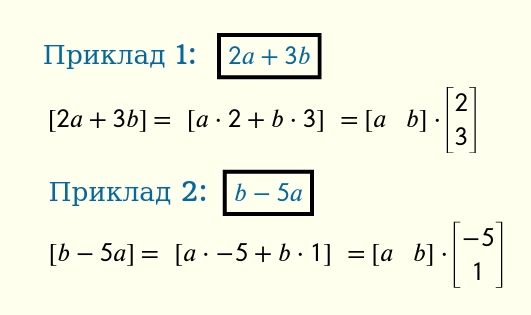
Думаю, на цьому етапі ваші думки такі: “виглядає нескладно. Коли ж уже буде м’ясо?"
Потерпіть ще трішечки. А краще, спробуйте зробити кілька завдань на визначення матриць обчислення. Можливо буде просто, а можливо доведеться подумати. Дуже рекомендую зробити це перед переходом до наступної теми.
Дано 1×2 матрицю [a b]. Потрібно знайти 2×1 матриці для обчислення наступних лінійних виразів:
1) 10a + 2b
2) - a - b
3) (a+b) / 2 (/ — це знак ділення, якщо що)
4) b
5) t·a - t·b + b (для будь-якого t)
6*) a + b + 1 (завдання з зірочкою!)
Це хороша практика для розуміння наступної теми — заплутаності!
Заплутаність
Як ви вже зрозуміли, матриці чудово годяться для додавання, віднімання та лінійних комбінацій чисел. Досліджуючи матриці реальних мікронейронок (мною навчених), я помітив, що нейронка рідко працює з власне вхідними числами a та b, а скоріше з їх лінійними комбінаціями.
Змінимо дещо попередні приклади.
Нехай у нас є 1×2 матриця з двох чисел, але не [ a b ], а яка складається з їх суми та різниці — X = [x1 x2], x1=a+b, x2=a-b. Потрібно визначити матриці обчислення виразів, використовуючи X:
2a + 3b
b - 5a
Хах! А це вже цікавіше. Перше питання, яке спадає на думку: чи це взагалі можливо? Так, можливо, але давайте спершу ви спробуєте зробити це як вправу:
Вправа: маючи 1×2 матрицю
X = [x1 x2] = [ (a+b) (a-b) ]
потрібно знайти такі 2×1 матриці M1 та M2, щоб справджувалися:
1) X·M1 = [ 2a+3b ]
2) X·M2 = [ b-5a ]
Як розв’язати ці задачі? Ті, хто добре знають алгебру, можуть скласти рівняння і знайти ці матриці, але можна розв’язати й іншими способами.
1) Зауважте, що 2a+3b = (a·2+b·2) + b = 2(a+b) + b = 2·x1 + b. Перший доданок вже готовий, залишається питання як зробити b через x1 та x2. Треба використати такий трюк:
(x1 - x2) / 2 = ((a+b) - (a-b)) / 2 = (a + b - a + b) / 2 = (2b) / 2 = b.
Тепер:
2·x1 + b = 2·x1 + (x1 - x2) / 2 = 2·x1 + 0.5·x1 - 0.5·x2 = 2.5·x1 - 0.5·x2
А це вже легко зробити у вигляді матриці.
2) З попереднього прикладу, ми знаємо, що
b = 0.5·x1 - 0.5·x2
але таким же трюком можна знайти і a
a = 0.5·x1 + 0.5·x2
Тоді:
b - 5a = 0.5·x1 - 0.5·x2 - 5(0.5·x1 + 0.5·x2) = -2·x1 - 3·x2
Ізі
З попереднього розділу ми знаємо, що з чисел можна порахувати їх суму та різницю — лінійним комбінаціями.
А з другого прикладу видно, що з суми чисел та їх різниці можна відновити оригінальні числа назад — лінійними комбінаціями.
Здогадуєтесь до чого я веду?

Давайте я назву перетворення чисел у їх суму та різницю — заплутуванням, а перетворення назад — розплутуванням. Оскільки це лінійні комбінації, то для них можна скласти матриці:

enc та dec — це скорочення від encoder та decoder. Я міг би називати речі своїми іменами, не “заплутування” і “розплутування”, а “кодування” і “декодування”, але погодьтесь, стало би менше романтики…
Ці матриці мають розмір 2×2, а не 2×1 як раніше. Можна вважати, що 2×2 матриця заплутування складається з двох матриць — 2×1 матриці додавання та 2×1 матриці віднімання. Ви бачите це?
Заплутування чисел справді рахує суму та різницю:

а розплутування справді відновлює наші числа назад:

Алгебра — вона працює. Ви помітили, як гарно вийшло?
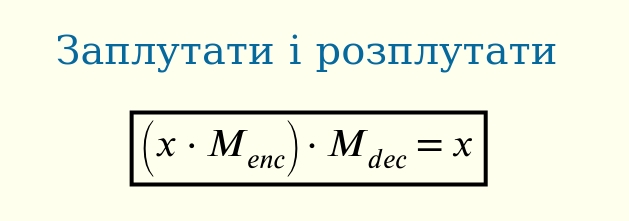
Але алгебра матриць має таку особливість, що дужки можна змінити, і порахувати цей вираз дещо інакше. Ми отримаємо новий екзмепляр в нашому зоопарку матриць, нейтральну матрицю, або матрицю, що нічого не робить:

Той факт, що дужки дозволено змінювати, математичною мовою називається “асоціятивність”.
Нейтральна матриця позначається як I (від англ. identity). Вона справді нічого не робить, і відіграє ту ж роль, що й число 1 при множенні чисел, або число 0 при додаванні чисел — зовсім не змінює результат.
Вправа з зірочкою: ви помітили, що M_enc та M_dec дуже схожі? Майже однакові, тільки друга матриця в 2 рази менша. Ваше завдання знайти таку матрицю H, яка буде схожа на ці матриці заплутування, але буде одночасно працювати і на заплутування, і на розплутування.
Тобто, x·H робить певним чином заплутування, і при цьому x·H·H = x. Або, іншими словами, H·H = I.
Спойлер: в результаті ви відкриєте вентиль Адамара з теорії квантових обчислень!
Все, що описано вище, це були тільки салатики. І якщо ви ще тут, то ви готові до м’яска.
Нейронки чхали на заплутаність
Нагадаю, як схематично працює розв’язування задач нейронками. Ви перетворюєте вашу задачу в набір чисел, “згодовуєте” його на́вченій нейронці, і вона видає на вихід підрахований результат.

Наприклад, якщо у вас є два числа, a та b, і ваша нейронка рахує вираз b-5a, то це виглядатиме так:

Але
Якщо ви спробуєте “заплутати” числа, і замість самих чисел дати на вхід їх суму та різницю, то нейронка все-рівно зможе навчитись виконувати задачу, навіть не знаючи, що числа були заплутані!
Навіть не знаючи!
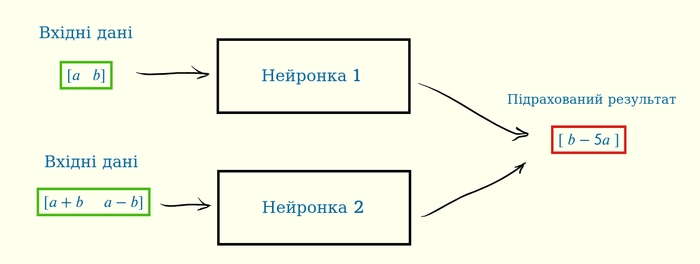
Конкретно в цих простих випадках ми можемо точно сказати, як виглядатимуть обидві нейронки (в ідеалі). Обидві будуть складатись з однієї матриці 2×1. Першу ми вже раніше складали, назвемо її M_1, а друга буде добутком двох матриць — M_dec та M_1:

Цей результат цікавий з людської точки зору. Перший варіант нейронки виглядає дуже “логічним” та “прямолінійним”. Прямолінійність цінується серед людей, бо так простіше передбачувати поведінку. Другий же варіант — це вже якесь ускладнення. Для чого це ускладнення? Навіщо взагалі цей варіант, хіба не можна було обійтись першим варіантом? Це ж додаткові дії, який у цьому задум? Хто заплутує вхідні дані, чи є у цього якась вища мета?
Тим не менш, при тренуванні практично будь-якої нейронки ви можете використати цей трюк: взяти і “заплутати” вхідні дані, just for fun. І нейронка навчиться робити вашу задачу, навіть по заплутаним даним.
Зауважу, що нейронка навчена на прямолінійних даних не зможе працювати на “заплутаних”, і навпаки. Їх внутрішні матриці повинні бути різні.
Проте це я поки-що говорив про нейронку, що складається з однієї матриці. Для наших іграшкових прикладів ми можемо її знайти ручками. Але справжні нейронки вчаться, і вчаться особливим алгоритмом…
“градієнтним спуском”, але насправді там є й інші алгоритми навчання нейронок: методи оптимізації нульового та другого порядків, еволюційний алгоритм, дистиляція.
…, і для нейронки з однієї матриці він знайде таке ж рішення як і у нас. Але що якщо нейронка складається з більше ніж однієї матриці, що вона “вивчить”? Це вже ближче до реальності, де нейронки мають десятки послідовних матриць.
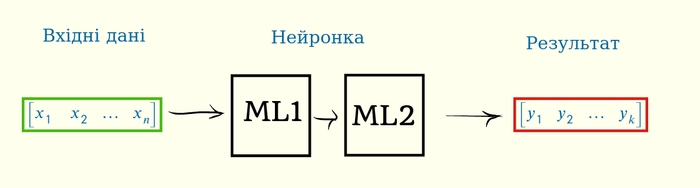
І тут я знову зроблю ліричний відступ, і спробую пояснити чому варто розглянути такий випадок. Якщо нашу нейронку “антропоморфувати”, ставитись до неї як до живої істоти, то різні етапи множення матриць мають людські відповідники.
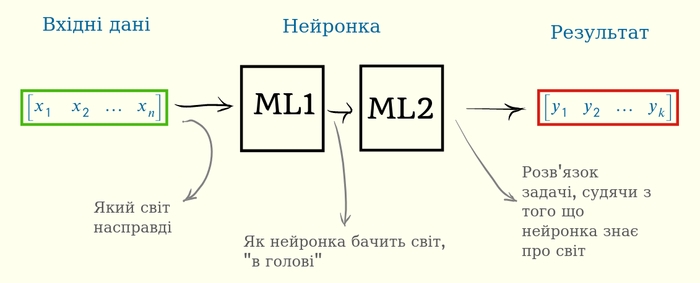
Наші вхідні дані — це реальний стан речей у світі. Ці вхідні дані проходять через перший шар нейронки ML1, де перетворюються у “зручний” для нейронки вигляд. І розрахунок результату вже йде саме від цього, “зручного” представлення.
Що ж тоді є “зручним” для нейронки? Ну ми знаємо, що для людини зручною є прямолінійність:
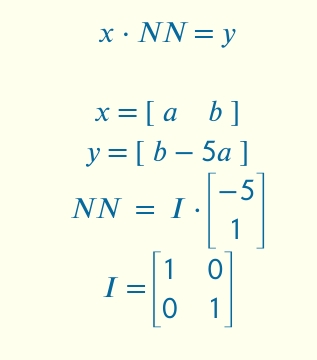
Як ми бачимо світ, так ми його і уявляємо в голові. Матриця I нічого не робить, але це якраз і задумано — навіщо робити більше?
А ось приклад, що вивчає нейронка:

Абсолютно дикі числа! Перша матриця робить якесь хитре перетворення, і, відповідно, нейронка бачить світ якось викривлено (з точки зору людини). Тим не менше, ця мікро-нейронка працює і рахує вираз b-5a. Це легко перевірити: -2.838×1.758-0.537×0.017 = -4.99 ~= -5, і 0.567×1.758+0.14×0.017 = 0.99 ~= 1, якраз ті числа в нашому прикладі лінійної кобмінації.
Взагалі, я натренував багато нейронок. Ось ще 10 з них
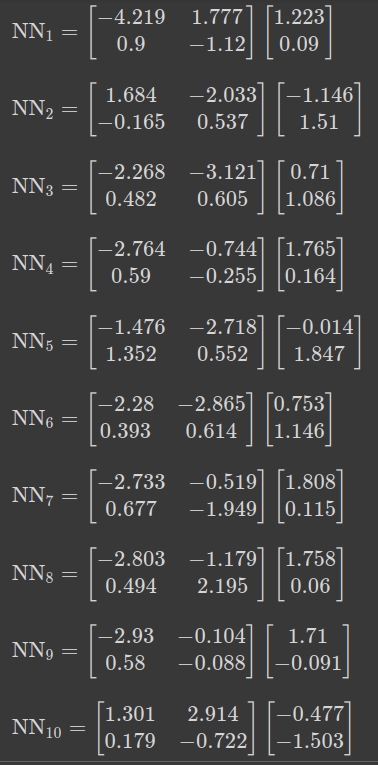
Ще 50 нейронок знаходяться тут, разом з кодом генерації:
https://colab.research.google.com/drive/1FbyFIoPoBceQvv_w5hTeMCSaODoum90j?usp=sharing
Вони всі більш-менш виконують свою роботу (більш-менш, бо деякі працюють не дуже точно, до 1% відхилення від точного результату). І при цьому ВСІ використовують “заплутування” вхідних даних, щоправда майже завжди не таке як я розглядав в попередньому розділі.
Хоча одна з нейронок, а саме NN10, близька до цього. Знаки біля чисел в матриці відповідають знакам в схемі заплутування.
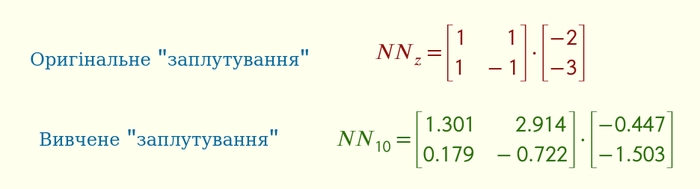
NN7 та NN4 також мають цю схему, якщо всі знаки поміняти на протилежні. Але всі інші нейронки — що́ вони вивчили, я́к вони “бачать” світ?
Вправа (відкрите питання): розібратись та каталогізувати схеми, які вивчають ці 2-матричні нейронки, які саме кодування вони використовують.
Хитро працює нейронка NN1. Я помітив, що в другій матриці одне з чисел близьке до нуля (0.09), а інше — близьке до одиниці (1.223). Це дає підказку, що́ саме намагалася вивчити нейронка:
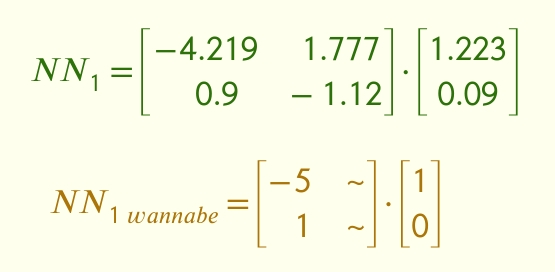
Тобто, матриця вивчила робити задачу в першій матриці, а друга матриця по факту вибирає тільки перший стовпчик. Це — спеціалізація. Якби матриця вивчила схему NN1wannabe, то її представлення світу (ось те, між матрицями) складалось би з однієї задачі. Це відрізняється від заплутування, бо в цьому випадку “розплутування” неможливе.
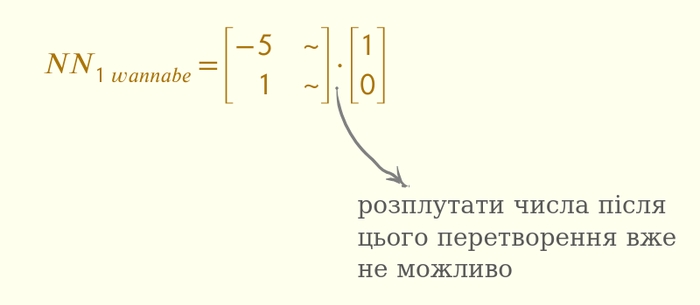
Технічною мовою ми кажемо, що після перетворення інформація може або зберегтись, або втратитись. Оригінальне заплутування інформацію про вхідні дані зберігає, а в випадку вище — інформація зменшується. Я колись довго вважав, що “інформація” — це просто абстрактне слово, проте все більше і більше знаходжу прикладів, що інформація — це більше як ресурс.
Заплутування та перетворення Гаара
Як ви вже здогадались, це “заплутування” вже було винайдено раніше, математиками. Ця матриця називається ненормалізована матриця Гаара.

Математики швидко впізнають це число 0.707, а інші спитають: чому саме це число? Справа в матриці розплутування, з цим числом 0.707 вона буде такою ж, як і матриця заплутування. Тобто, одна й та сама матриця як і заплутує, так і розплутує числа:

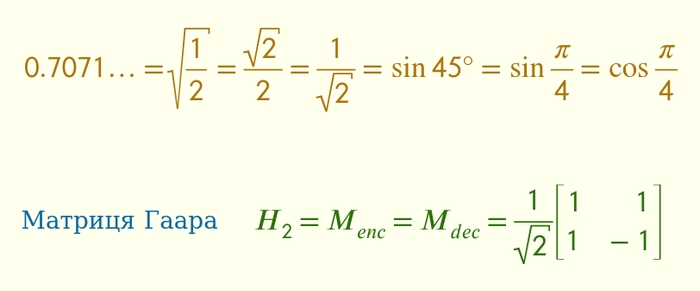
Інші приклади заплутування
Не зовсім кореткно називати цю матрицю саме матрицею Гаара. Справа в тому, що багато інших варіантів заплутування двох чисел також мають точно такий же вигляд. Ось як вони виглядають:

Перші 4 названі в честь математиків — Альфред Гаар, Жак Адамар, Джозеф Уолш та Жан Батист Жозеф Фур’є — а останнє запам’яталось саме як “дискретне косинусне перетворення”, хоча у нього також був автор — Насір Ахмед.
Вся математика на даний момент придумана людьми, тому це нормально давати назви в честь відкривача або когось дуже дотичного. Чи буде ця традиція продовжуватись в майбутньому?
Ці перетворення можуть заплутувати більше ніж 2 числа, власне тоді вони і починають відрізнятись:

Ці 4×4 матриці зовсім не випадкові, і навіть споріднені між собою різноманітними закономірностями:
матриці заплутування/розплутування повністю одинакові для Адамара та Уолша
якщо переставити деякі рядки місцями в матриці Адамара, то вийде матриця Уолша
матриця Фур’є використовує комплексні числа, тому не дуже зручна для нейронок. Всі інші працюють зі звичайними числами
матриці розплутування для всіх, окрім Фур’є, — це транспоновані матриці заплутування. Колонки однієї — це рядки іншої матриці
Гаара — це єдина матриця, де є нулі
всі матриці розплутування можна використовувати для заплутування також. Їх матричний добуток — це нейтральна матриця.
Якщо ви програміст/-ка, можете глянути на код реалізації всіх цих трансформацій: https://colab.research.google.com/drive/1Nw5ExpB-Sza-tcZEM7jywdyBVUrojtIa?usp=sharing
Всі ці перетворення можна візуалізувати на конкретному прикладі. Моя картинка (матриця з чисел розміром 32×32) має ширину 32 пікселя, а отже заплутування/розплутування елементарно робиться матричним добутком на відповідну 32×32 матрицю.
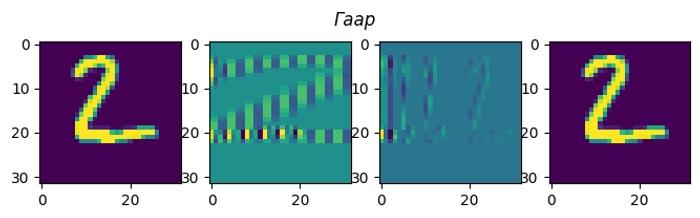
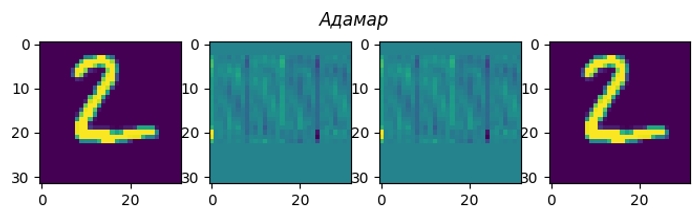
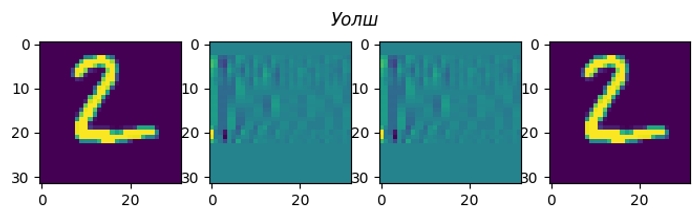
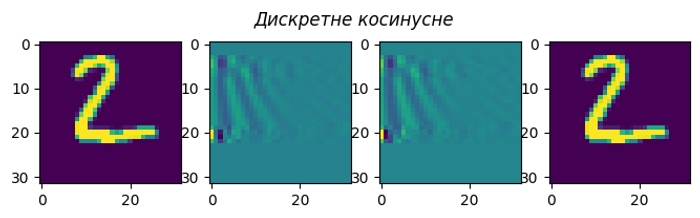
Я пропустив перетворення Фур’є, бо з комплексні числа незручно візуалізовувати. Косинусне перетворення найближче до нього, і при цьому дуже практичне.
Насправді, я не обмежений в кількості заплутувань своєї картинки. Кожне заплутування зберігає всю інформацію, тому якщо я зроблю розплутування в зворотньому порядку, то отримаю назад свою картинку.


Якщо на кожному етапі кодування додавати у закодовану картинку шум, то цей шум з’явиться і в декодованій картинці.


Як бачите, окрім цих 5 іменованих способів заплутати дані, можна зробити ще нескінченну кількість нових — просто перемножуючи ці 5 у певному порядку ми створюємо новий, абсолютно новий спосіб заплутування з допомогою однієї матриці!
Вправа (відкрите питання): чи справді нескінченну?
З’єднаємо тепер всі елементи нашого пазлу.
Нейронки чхали на заплутаність, ще раз
Один з типів нейронок, а саме MLP, multi-layer perceptron, багатошаровий перцептрон, складається з послідовності матриць та активацій, які, власне, в цій послідовності і перемножуються.
При навчанні ми ніяк не обмежуємо що саме вчить кожна конкретна матриця. В тому числі не обмежуємо що вчить перша матриця. Що вона вивчить? Які числа будуть в цій матриці?
Моя гіпотеза в тому, що в першій матриці вона вивчає певне “зручне” заплутування. Зручне в тому сенсі, що задача має простіше рішення в заплутаному, аніж в оригінальному вигляді. Але це також означає, що якщо дати на вхід заплутані дані, нейронка може їх “розплутати”, якщо це буде їй зручніше.
Причому, доки наше заплутування має вигляд матриці, неважливо як саме ми заплутуємо.
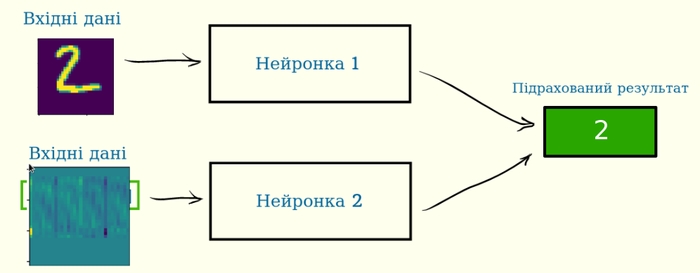
Навіть більше, заплутування можна зробити будь-якою комбінацією будь-яких матриць трансормації, які я описував вище. І все-рівно нейронка зможе навчитись розрізняти числа (якщо ми вчимо її розрізняти числа, звісно). Нейронка зможе частково розплутати ці дані, хоча навіть не буде знати як саме вони заплутані.
Нам, людям, важко такому навчитись.
А нейронці все-одно. Вона навчиться. Вибере собі зручне представлення.
Бо це всього лиш матриця.
Ще одна матриця в добутку матриць, і більш нічого.

Завершення
Повторю основні ідеї всього довгочиту.
Матриці та матричний добуток — це класно.
Одна операція (матричний добуток) може зробити так багато різних цікавих штук.
Хто має суму та різницю чисел — той також має числа.
Як кодування, так і розкодування легко записати матрицями.
Окрім цього, існують й інші перетворення чисел, при яких інформація не втрачається, і їх може використовувати нейромережа.
Теорія інформації, теорія кодування та теорія цифрових сигналів як раз і займаються дослідженням тем — як перетворити, зберегти, зменшити, захистити інформацію.
Якщо дані на вході нейромережі закодувати якимось матричним заплутуванням, нейромережа все-рівно зможе навчитись виконувати задачу.
Бо це всього-лиш ще одна матриця в ланцюжку матриць.
Нейронка в процесі роботи перетворює вхідні числа у зручний вигляд.
Зручний для нейронки, а не для людини!
Використані матеріали:
Вейвлет Гаара: https://en.wikipedia.org/wiki/Haar_wavelet
Дискретне косинусне перетворення: https://en.wikipedia.org/wiki/Discrete_cosine_transform
формули для матричних перетворювань сигналів: https://www2.seas.gwu.edu/~ayoussef/cs225/transforms.html
Властивості перетворень: https://slideplayer.com/slide/14991129/
Картинки зроблено в https://inkscape.org/
Формули зроблено в https://app.idroo.com/
Код написано в https://colab.research.google.com/
Що далі?
DCT це дуже, дуже крутий та популярний алгоритм. Він один з найближчих до оптимальних (з точки зору декореляції та компактизації енергії). На його основі працюють практично всі кодеки картинок, аудіо та відео.
Матричні перетворення не тільки можуть кодувати дані. Якщо вистачить сил, розпишу ще про одне дуже важливе перетворення — пермутацію.
Всі ці заплутування пов’язані з квантовими алгоритмами. В квантовому світі інформація не може просто так зникати, тому всі квантові вентилі мають її зберігати. Тому всі варіанти заплутування можуть мати квантові відповідники! Оригінальне 2×2 заплутування навіть має назву “вентиль Адамара”.
Окремо треба проговорити про біаси та ReLU. Ці частини нейронки дуже важливі для її роботи, і з ними перетворення між шарами нейронки більше не зберігають інформацію. Точніше, все складно :/, але не безнадійно.
Треба дослідити, чи описане вище відноситься до конволюційних нейронок.
Хоч нейронка сама вивчає “зручне” собі представлення вхідних даних — ми можемо дещо управляти цим процесом, це основна ідея sparse coding.
