Задача про розклад уроків 📚
Уявімо, що у нас є навчальний клас, у якому треба провести якомога більшу кількість уроків.
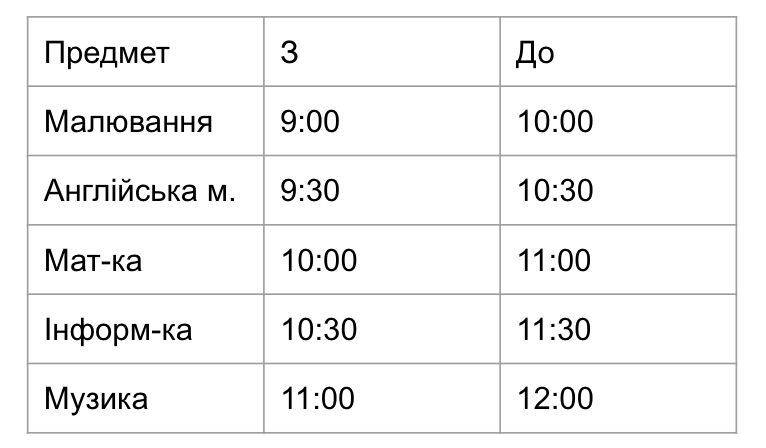
Провести всі уроки в класі не вийде, адже деякі з них пересікаються за часом.
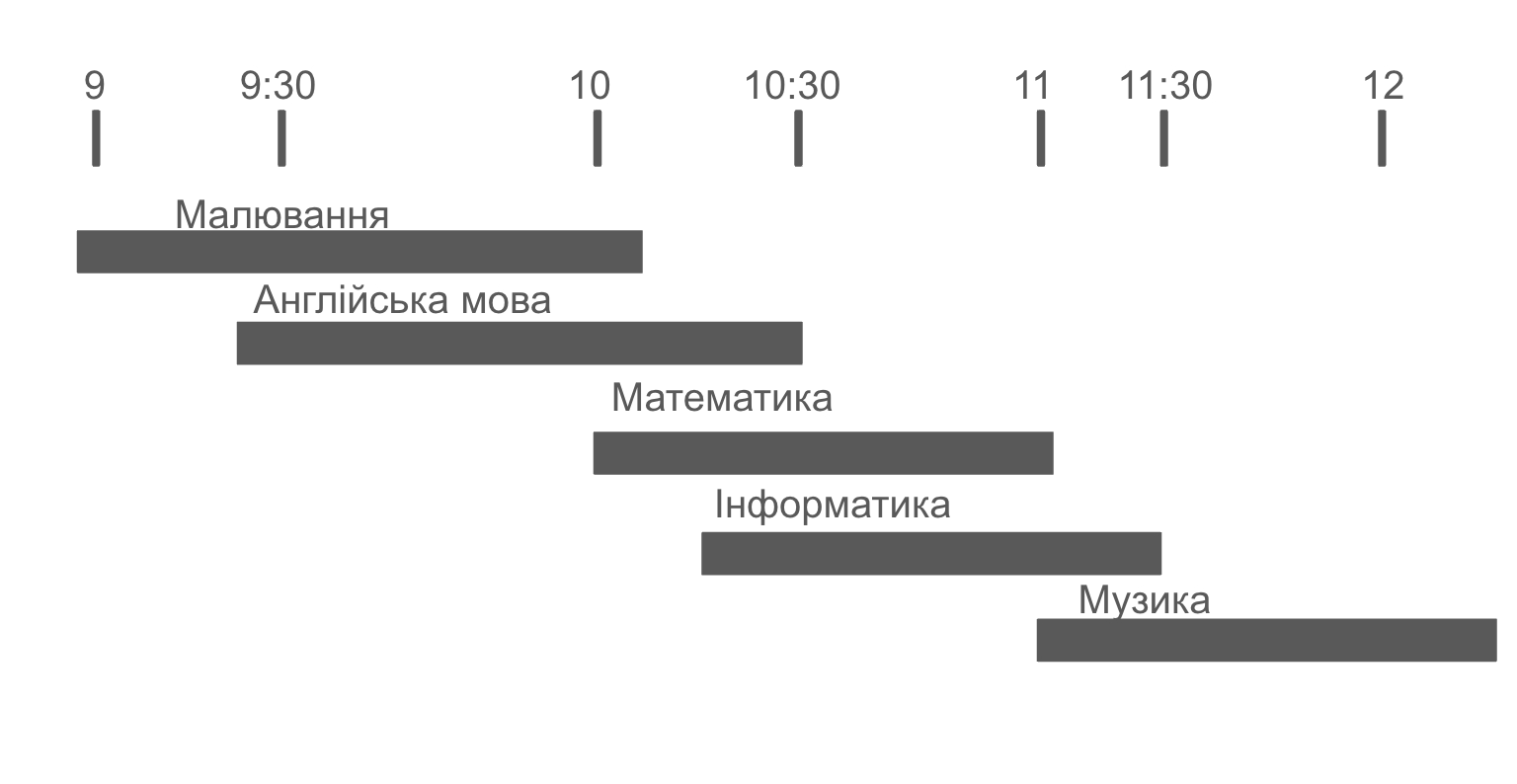
Основною умовою є проведення у класі якомога більше уроків. Як обрати уроки, щоб отриманий набір виявився найбільшим із усіх можливих?
На допомогу приходить жадібний алгоритм. Працює він наступним чином:
1. Обрати урок, який закінчується раніше за всі інші. Це перший урок, який буде проведено в класі.
Наступним кроком необхідно обрати урок, який починається по завершенню першого уроку. І знову необхідно обрати урок, який закінчується раніше за інші. Він буде другим у розкладі.
Продовжувати виконувати 2 крок алгоритму допоки не закінчиться список уроків - і ви отримаєте відповідь!
Спробуємо використати алгоритм на нашому прикладі. Ми можемо побачити, що малювання закінчується раніше за всі інші уроки ( о 10:00), тому його ми й оберемо першим уроком.
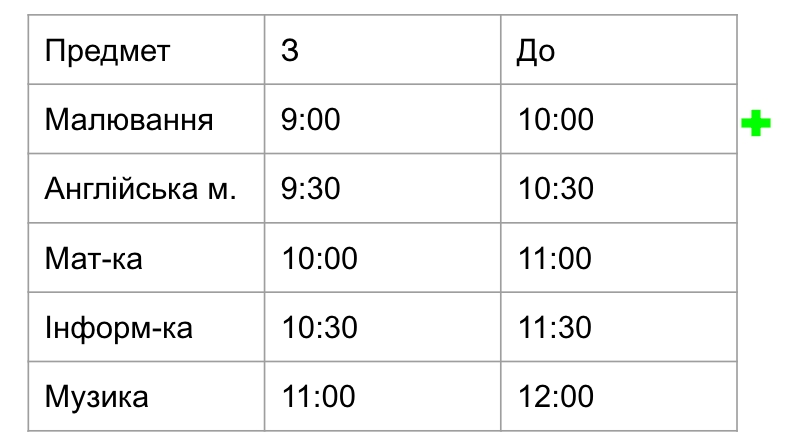
Тепер необхідно знайти наступний урок, який починається після 10:00 і закінчується раніше за всі інші.
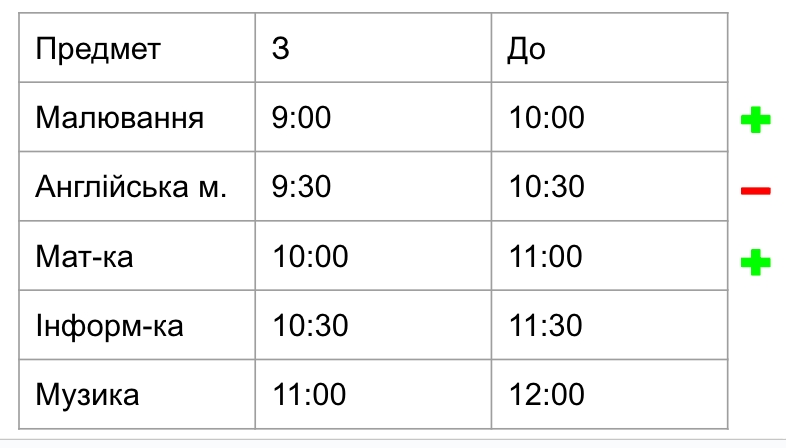
Англійська мова відпадає, бо її початок пересікається з малюванням. Проте математика підходить. Нарешті, інформатика має перетин із математикою, а ось музика може бути третім уроком.
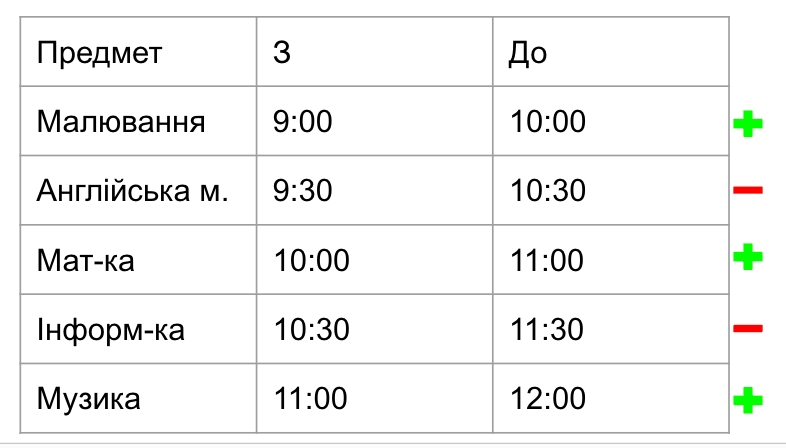
Отже, розклад матиме наступний вигляд:
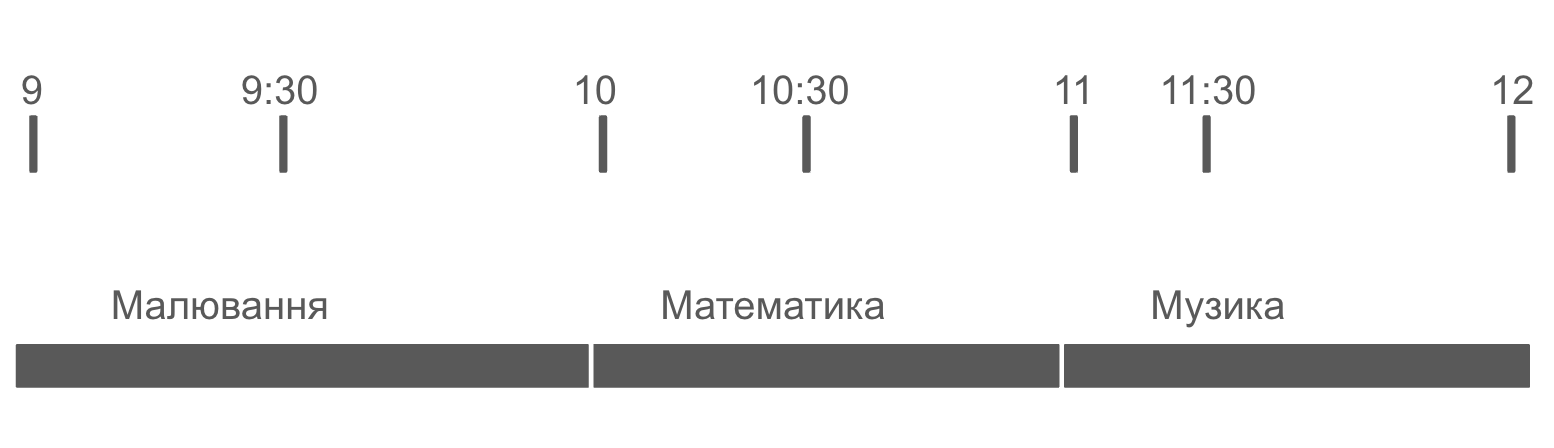
Жадібний алгоритм достатньо простий: на кожному кроці він обирає оптимальний варіант. У нашому прикладі, він обирає предмет, який завершиться раніше за всі інші. В технічній термінології: на кожному кроці обирається локально-оптимальне рішення, а, як результат, ви отримуєте глобально-оптимальне рішення. Цей алгоритм знаходить оптимальне рішення задачі зіставлення розкладу.
