Задача про комівояжера ( в оригіналі ), але я пропоную додати ноток реальності та розібрати задачу про фургон Нової Пошти.
Умова
Умова задачі: припустімо, фургон Нової Пошти має відвідати 5 міст. Треба знайти найкоротший шлях, який містить у собі всі 5 міст. Для того, аби знайти найкоротший шлях, спочатку необхідно розрахувати всі можливі варіанти шляхів.
Скільки маршрутів необхідно розрахувати для 5 міст?
Кроки вирішення
Давайте розбиратися з цією задачею крок за кроком.
2 міста
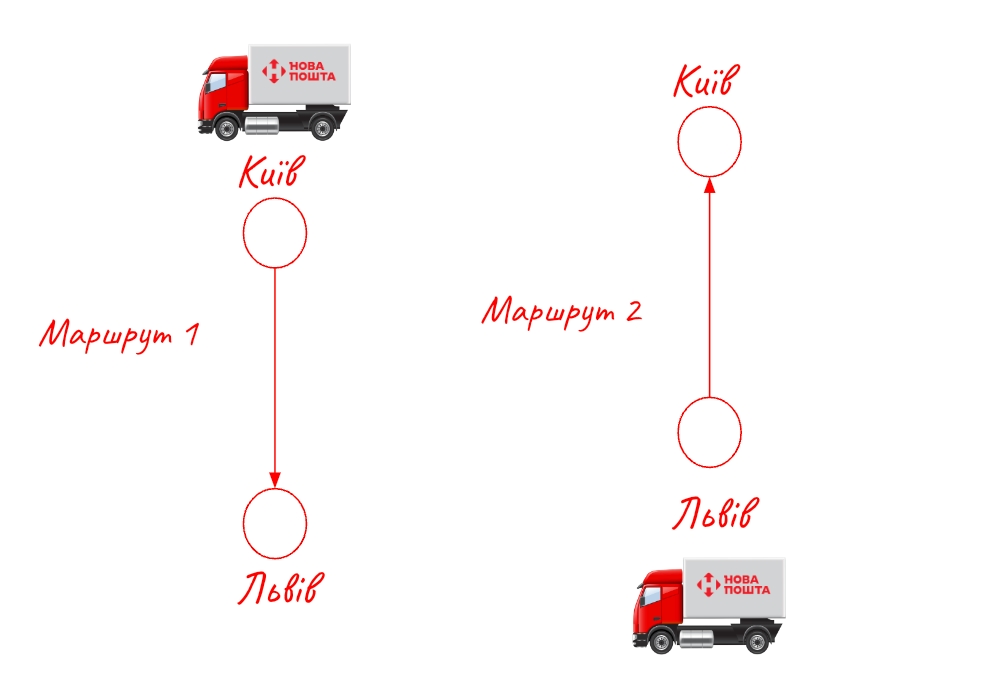
Пропоную розпочати з меншої кількості міст. Наприклад, 2 міста - Київ та Львів. Обирати доведеться всього з 2-ох маршрутів.
Side Questions, які могли виникнути:
Чи існує конркетне місто, з якого треба починати наш маршрут?
У даній ситуації ми вважатимемо, що обраного початкового міста не існує.
Хіба відстань від Києва → Львова та від Львова → Києва не співпадає?
Ми будемо припускати, що не завжди. Наприклад, якщо уявити, що у місті є багато вулиць з одностороннім рухом, то нам не вдасться повернутися по тому ж шляху, по якому ми приїхали. Іноді доводитиметься проїзжати декілька додаткових км для того, аби знайти виїзд на шосе. Отже, ми вважатимемо, що ці 2 маршрути не завжди співпададимуть за довжиною.
3 міста
Що буде, якщо ми вирішемо додати 3 місто? Скільки можливих маршрутів існуватиме в такій конфігурації? Додамо місто Харків.
Якщо ми починаємо з Харкова:
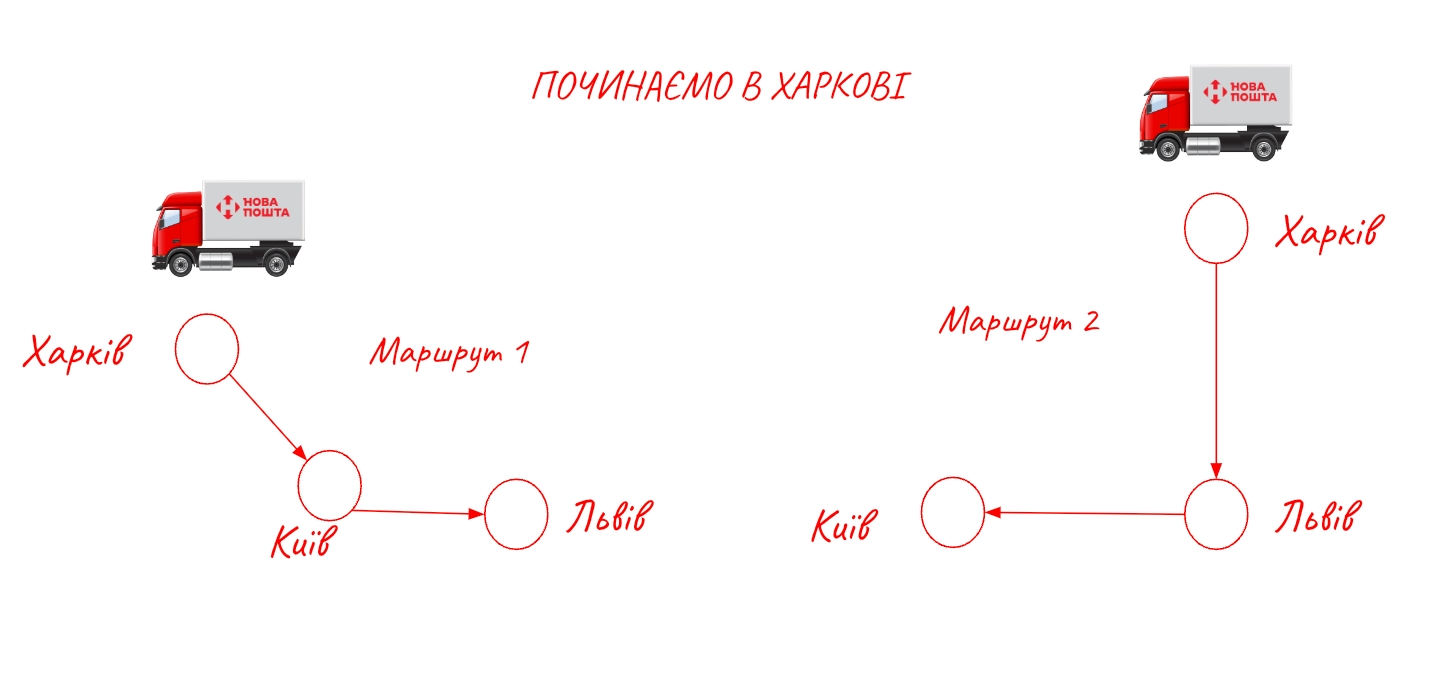
І поки ви не почали засуджувати це геніальне логістичне рішення поїхати із Харкова до Львова, а потім зі Львова до Києва, зробимо висновок, що всього буде 6 можливих маршрутів: по 2 для кожного міста, з якого ми можемо почати.
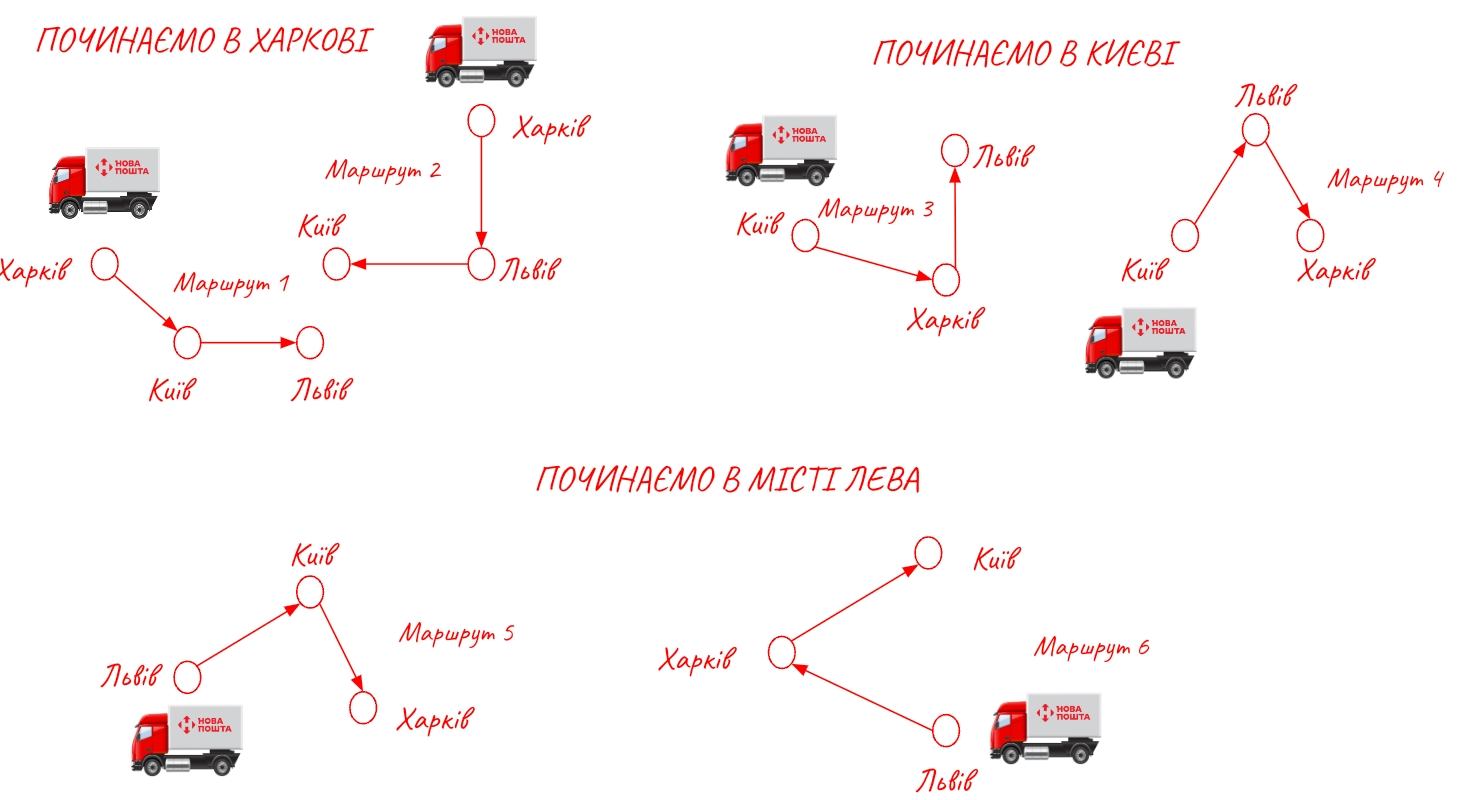
Отже, 3 міста = 6 можливих маршрутів.
4 міста
Час додати 4 місто - Одесу. Тепер припустімо, що саме з неї ми і почали.
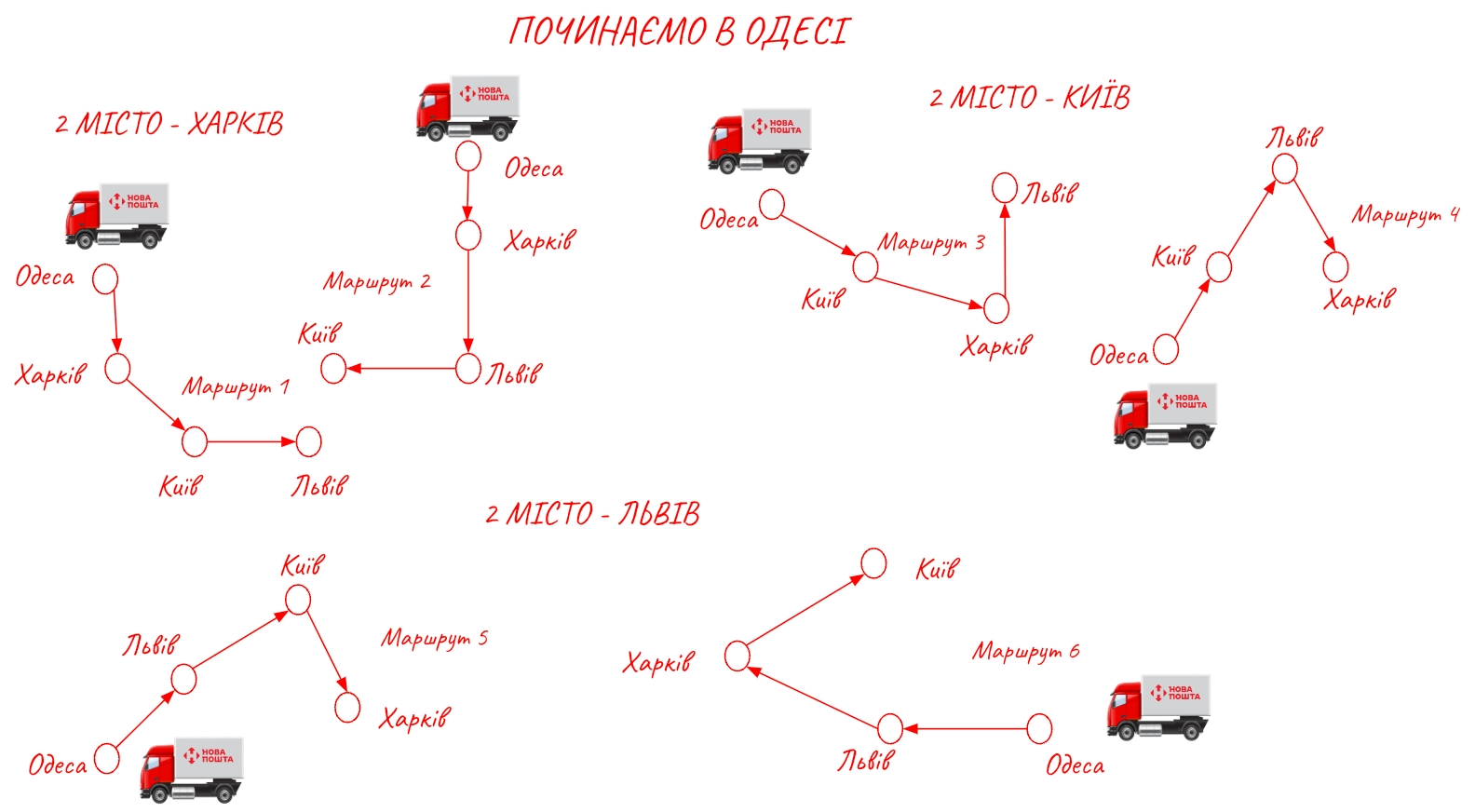
Тож, якщо ми починаємо в Одесі, то маємо 6 можливих маршрутів. Так, вони дуже схожі на ті 6 маршрутів, які були вираховані на попередньому кроці. Але тоді було 3 міста, а зараз до них додалось ще одне (четверте місто) - Одеса. Починає з’являтися закономірність. Припустімо, що з 4 міст першим ви обрали Одесу. Залишається ще 3 міста. І ми знаємо, що для того, аби переміщатися між 3 містами є 6 можливих маршрутів. Тобто, якщо ми починаємо з Одеси, то мажмо 6 можливих маршрутів. Так само можна почати з одного із інших міст.

4 початкових міста, 6 можливих маршрутів для кожного початкового міста = 4 × 6 = 24 можливих маршрути.
5 і > міст
Помічаєте закономірність? Кожен раз, коли ви додаєте нове місто, збільшується к-сть розрахованих маршрутів.
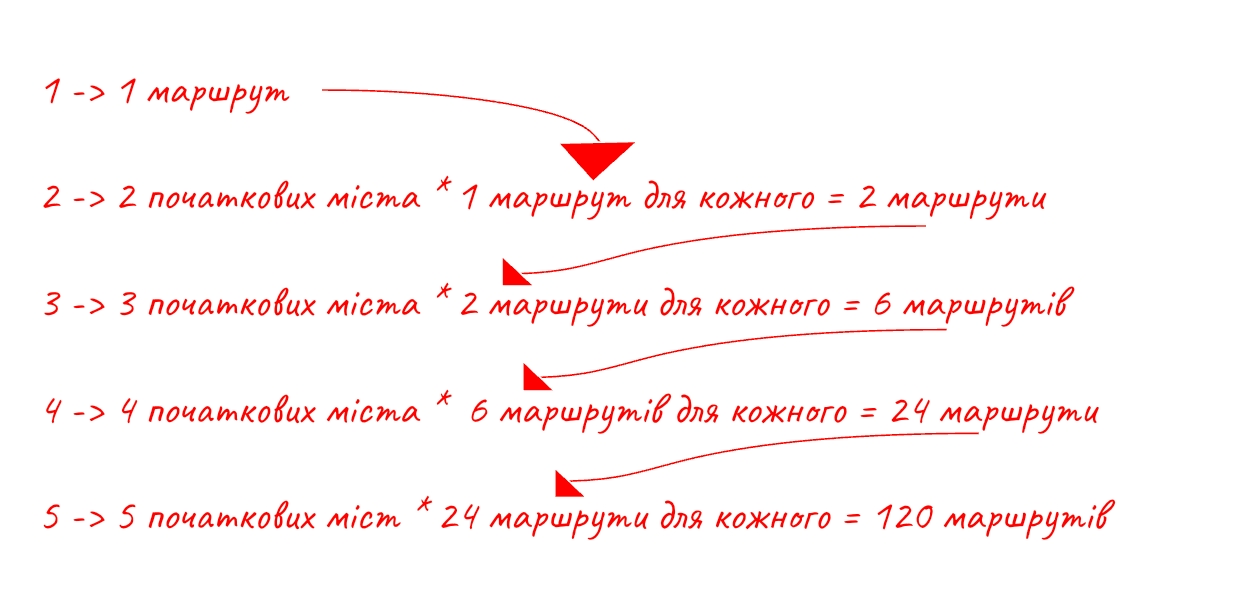
Скільки маршрутів існує для 7 міст? 720, кажете? Так, ви маєте рацію. 5040 для 7 міст, 40 320 для 8.
Така залежність називається факторіальною. 5! = 120. Припустімо, є 10 міст. Скільки існує можливих маршрутів? 10! = 3 628 800. Уже для 10 міст необхідно розраховувати більше за 3 мільйони можливих маршрутів. Як бачите, кількість можливих маршрутів стрімко зростає. Саме тому неможливо знайти “правильне“ рішення задачі про фургон Нової Пошти за дуже великої кількості міст.
Ця задача є NP-повною. Деякі задачі відомі через складність їх вирішення. Задача про комівояжера ( фургон НП ) - класичний приклад. Деякі експерти вважають, що знайти швидкий алгоритм для вирішення таких задач неможливо.
Наближене рішення
Як виглядає наближений алгоритм вирішення задачі про комівояжера ( або про фургон Нової Пошти)? Це повинен бути простий алогритм, який знаходить найкоротший шлях.
Рішення може бути наступнми: початкове місто обирається довільно. Після чого, кожен раз, коли комівояжер ( фургон НП) обирає наступне місто, він переміщається у найближче місто, серед тих, у котрому він ще не був. Як ви могли здогадатися - це жадібний алгоритм!)
Можливо це не буде найкоротший шлях, але такий шлях буде дуже близький до найбільш оптимального рішення.
Підсумок
~ Жадібні алгоритми прагнуть до локальної оптимізації із розрахунком на те, що в результаті буде досягнуто глобального оптимуму
~ У NP-повних задач немає відомих швидких рішень
~ Якщо у вас є NP-повна задача, то найкраще використати наближений алгоритм вирішення
~ Жадібні алгоритми легко реалізуються і швидко виконуються, тому із них виходять хороші наближені алгоритми
Питання для розігріву
Для кожного із наведених нижче алгоритмів вкажіть, чи є даний алгоритм жадібним чи ні:
Швидке сортування.
Пошук у ширину.
Алгоритм Дейкстри.
