Neural Network [guide] 1

Вступ

Нейронні мережі як і будь які інші творіння людей були створені із ідеєю - покращити та спростити життя людям.

Генеративний ШІ показує колосальні успіхи. Всі хто перший раз спробував спілкуватись із GPT4, Bard чи іншими, розуміють ці цікаві емоції.

Якщо спробувати погуглити курси по нейронних мережах, ви обов’язково знайдете щось типу: TensorFlow, Keras, Pandas - це інструментарій який забезпечить вас набором готових рішень, вам потрібно лише мати набір даних та розуміння задачі яку ви вирішуєте.

Читаючи документацію цих бібліотек можна побачити купу незрозумілих термінів які зазвичай просто пропускаються тому що розбирати все це не дуже цікаво, а от написати нейронку яка буде уміти робити все за людей - це цікаво.

Сьогодні про те з чого все починається, нам знадобиться лише python.

Головні задачі які можуть вирішувати нейронні мережі це:

1. Класифікація - сьогодні не про це

2. Регресія - Сьогодні про це

Задача

Задача яку будемо вирішувати, потрібно знайти коефіцієнт лінійної функції знаючи “x” та “y”

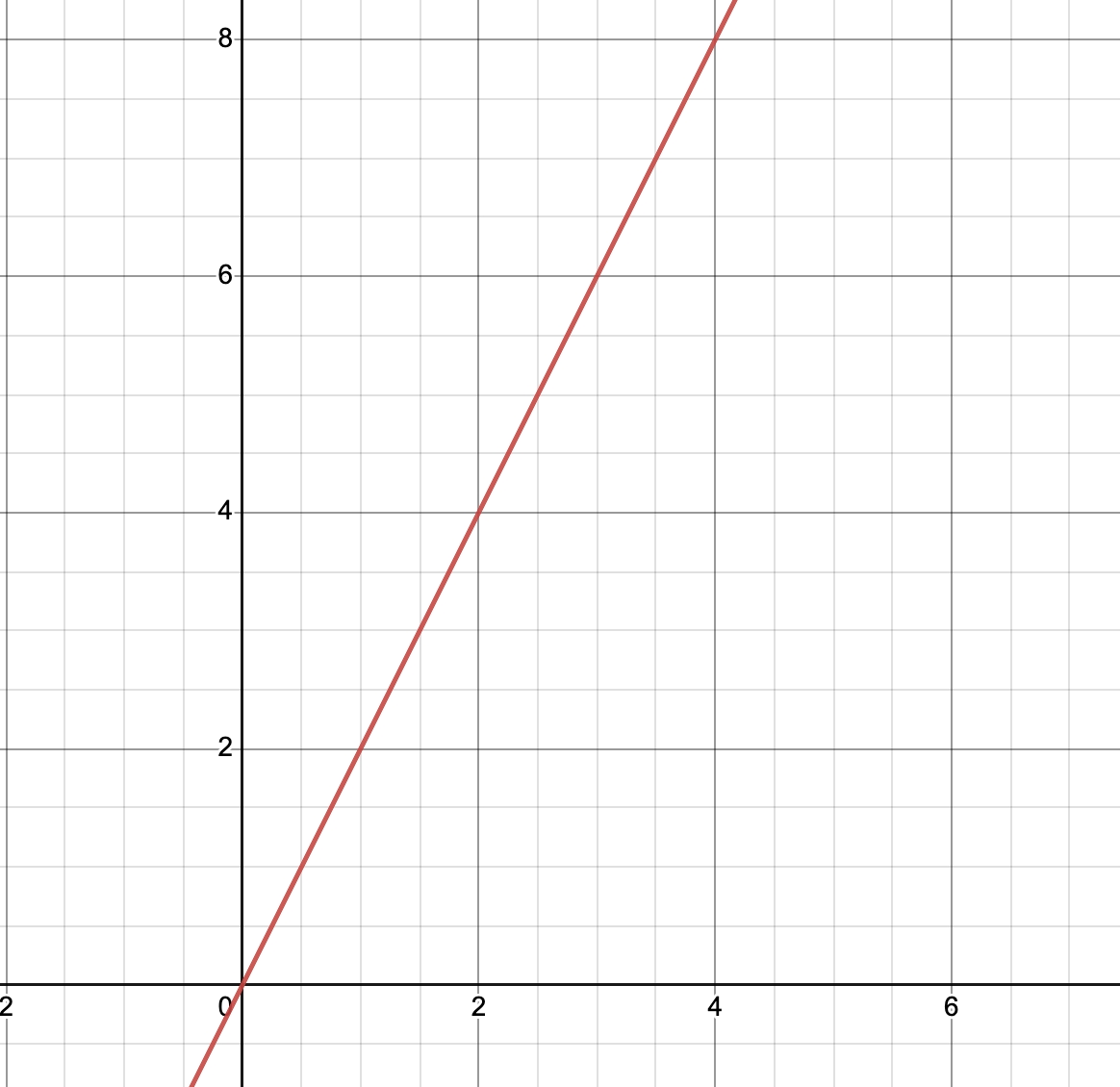
Для вирішення такої задачі нам знадобиться:

1. python

2. вхідні та вихідні дані

3. один нейрон

Вхідні дані

inputs = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10] // наші ікси
targets = [2, 4, 6, 8, 10, 12, 14, 16, 18, 20] // наші ігрики

Не складно зрозуміти що лінійна функція виглядає так:

y = x * 2;

але нам потрібно знайти “2" використовуючи засоби і алгоритми нейронних мереж.

Підготовка змінних

count = 10 // кількість елементів у вхідних та вихідних масивах
coefficient = 2 // будемо використовувати лише для генерації данних

inputs = [n + 1 for n in range(count)]
targets = [i * coefficient for i in inputs]

звичайна підготовка даних, це для зручності, у подальшому можна зробити окремі функції, для підготовки тестових даних або для зручного управління вхідними та вихідними даними.

Ключові утиліти

EPOACH = 10 // кількість епох для навчання
w = 0.1 // це початкове значення нашого коефіцієнту

def predict(i):
  return w * i

EPOACH - змінна для управління кількістю епох на яких наш нейрон буде навчатись

predict - функція для передбачення значення коефіцієнту, ще називають функцією активації (activation function), для наших даних достатньо самої простої лінійної функції активації.

w - weight, вага величини яка привела значення інпуту до значення таргету (шуканий коефіцієнт). Як це виглядає на картинці (A) - це inputs, (C) - це targets. Ми шукаємо (w) - коефіцієнт. В залежності від даних початкове значення цього параметру краще задавати невеликим, орієнтуйтесь на початкове значення target, від цього залежить швидкість навчання і кількість епох яку потрібно пройти, також занадто мале або занадто велике початкове значення може привести до неочікуваних проблем.

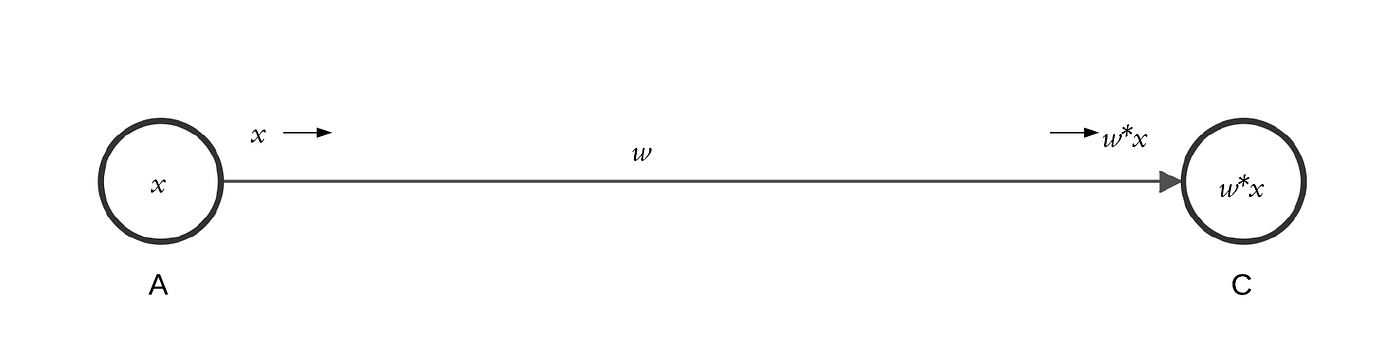
На даному етапі цього достатньо.

Алгоритм навчання

for _ in EPOACH:
  pred = [predict(i) for i in input]
  errors = [t - p for t, p in zip(target, pred)]
  cost = sum(errors) / len(targets)
  print(f"Weight: {w:.2f}, Cost: {cost:.2f}")
  w += cost

розберемось із цим:

pred - масив наших потенційних вихідних даних, які ми отримали прогнавши вхідні дані через лінійну функцію активації.

errors - це масив погрішностей, так як ми знаємо вихідні дані, ми віднімаємо від кожного таргету, predic значення щоб отримати результати які будуть враховуватись для уточнення значення (w).

cost - коефіцієнт помилки, це загальне значення нашої помилки, за допомогою цього значення ми і будемо корегувати наш (w)

w += cost - корегування (w)

Розходження графіку:

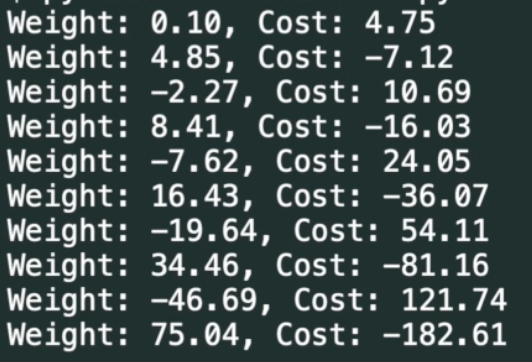
Значення Weight - дуже стрімко змінюється (що не добре), значення Cost - відповідно змінюється по експоненті, що теж є поганим знаком.

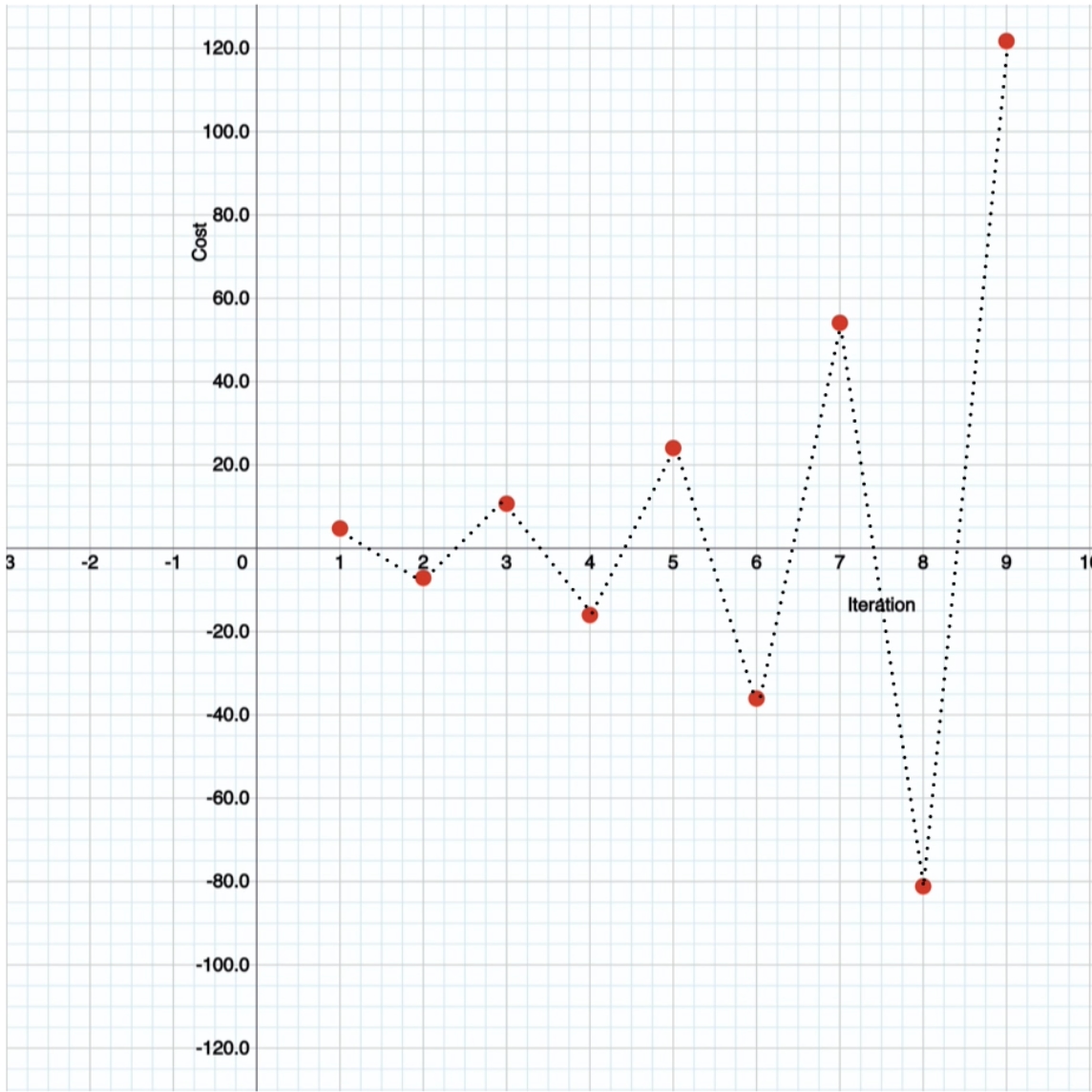
На графіку отримаємо такий результат - це називається “linear regression oscillating pattern"

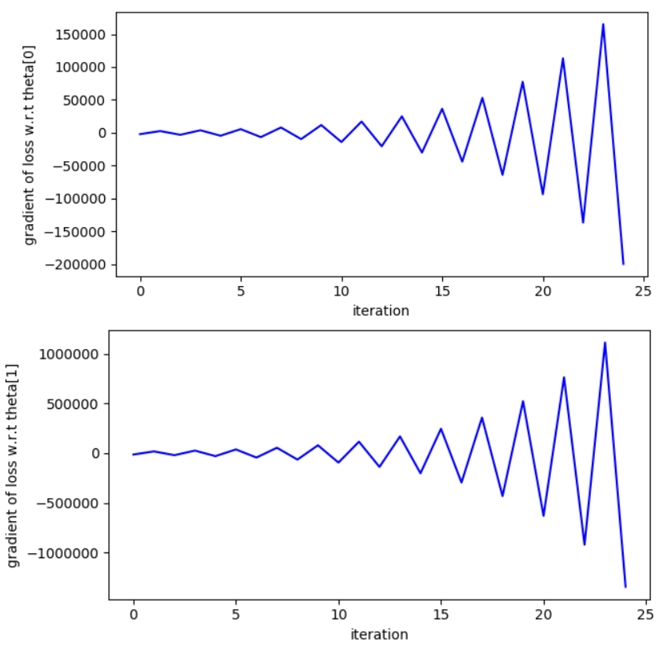
Як це виправити ?

Правильно запитати “Чому це відбувається ?" - це відбувається через наше фінальне коригування w += cost воно занадто велике і так як ми не завжди отримуємо позитивне значення відношення передбачених значень до вихідних - наш графік дуже сильно розходиться і це розходження буде тільки рости в залежності від кількості епох.

Щоб це виправити, нам потрібно додати ще один параметр, який буде додавати більшу гнучкість (для управління швидкістю навчання нашого нейрону).

learning_rate = 0.01

тепер у алгоритмі, виправимо тільки останній рядок коду:

for _ in EPOACH:
  pred = [predict(i) for i in input]
  errors = [t - p for t, p in zip(target, pred)]
  cost = sum(errors) / len(targets)
  print(f"Weight: {w:.2f}, Cost: {cost:.2f}")
  w += cost * learning_rate

w += cost * learning_rate - Додасть гнучкість, за рахунок цього наш коефіцієнт (w) буде змінюватись лінійно.

Запускаємо:

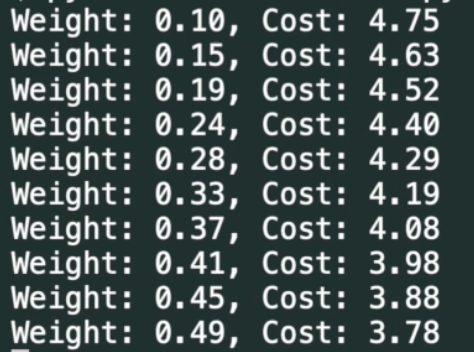
Тепер ми бачимо що дані змінюються лінійно - це дуже добре, але наша ціль щоб Cost дійшов до нуля, по зображенню можна побачити що при зменшенні Cost збільшується Weight .

Тепер нам потрібно підібрати правильне співвідношення кількості ітерацій (EPOACH) до значення (learning_rate), це не складно. Потрібно звернути увагу на те як швидко змінюються значення, якщо значення змінюються занадто повільно - збільшіть (learning_rate), якщо занадто швидко - зменшіть (learning_rate). Якщо значення змінюються лінійно і пропорційно то змінюйте кількість ітерацій (EPOACH) або якщо бачите що Cost = 0; а Weight = 2 на останніх ітераціях - зменшіть кількість ітерацій (EPOACH).

Нам потрібно збільшити learning_rate = 0.1 і замінимо значення EPOAH з 10 на 15.

EPOACH = 15

Стартуємо:

Всього за 15 ітерацій ми знайшли значення ваги (коефіцієнт) для наших даних.

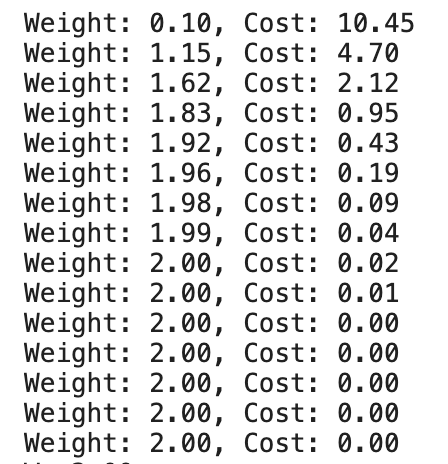
На графіку це виглядає так:

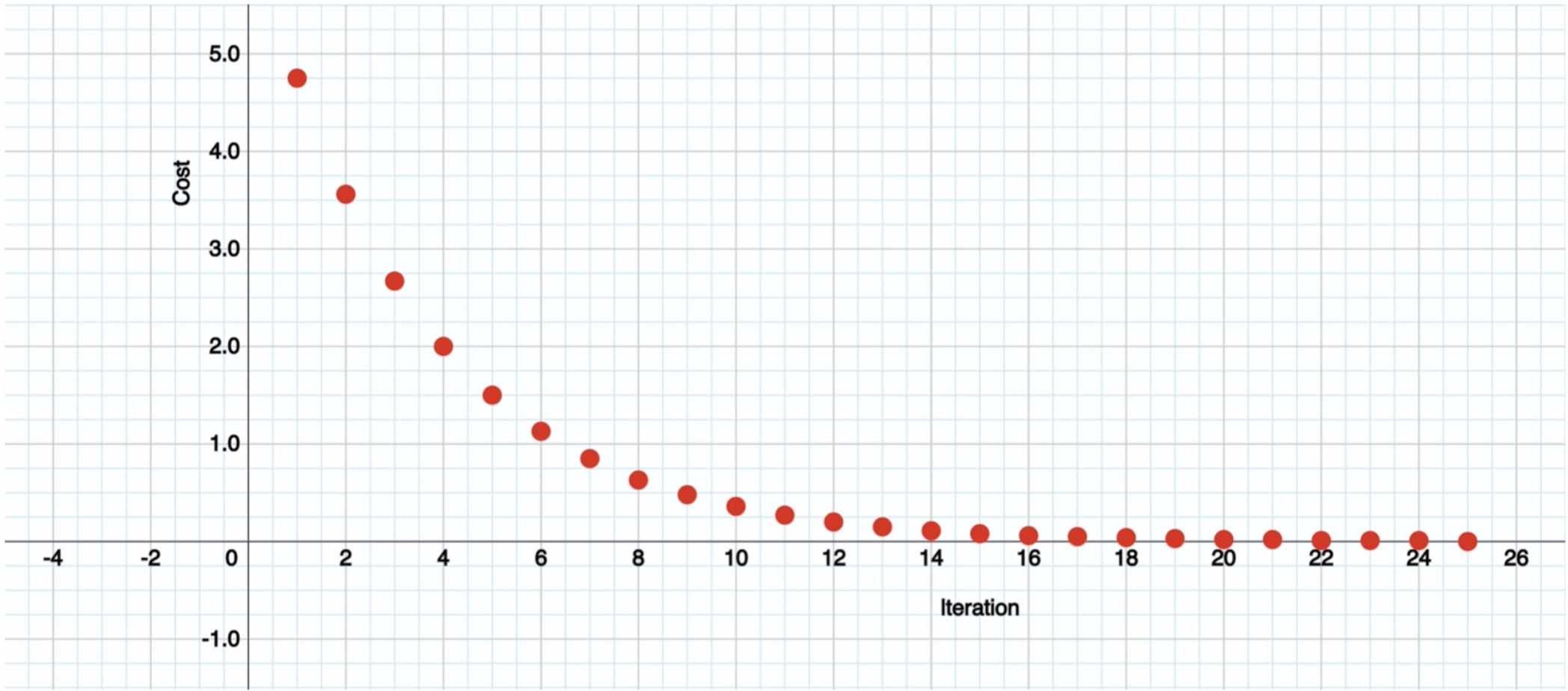
На цьому наша перша нейронна мережа з одним нейроном готова.

Фінальний код

count = 10
coefficient = 2
EPOACH = 15

inputs = [n + 1 for n in range(count)]
targets = [i * coefficient for i in inputs]

w = 0.1
learning_rate = 0.1

def predict(i):
  return w * i

for _ in EPOACH:
  pred = [predict(i) for i in input]
  errors = [t - p for t, p in zip(target, pred)]
  cost = sum(errors) / len(targets)
  print(f"Weight: {w:.2f}, Cost: {cost:.2f}")
  w += cost * learnning_rate

print(f"Final weight is {w:.2f}":);

20 рядків коду і ні одної умови, це як мінімум круто.

Підсумки

Якщо місцями це здається складним - це нормально, але це те що програмісти називають “якось працює під капотом", дуже не люблю коли так говорять.

Я пропустив деякі терміни, не хотів щоб ця стаття була тільки теоретичною.

Тут можна взяти код

Neural Network sample 1 · GitHub

Neural Network sample 1. GitHub Gist: instantly share code, notes, and snippets.

gist.github.com