Всіх вітаю! У сьогоднішній статті ми поговоримо про те, як реалізувати добуток Кронекера у Python завдяки бібліотеці numpy. У рамках цієї статті ми розглянемо як використовувати функцію kron() та у чому суть добутку Кронекера.
Теорія та підготовка
Що таке добуток Кронекера?
Добуток Кронекера — це такий добуток, у ході якого множенням кожного елемента першої матриці на всю другу матрицю ми отримуємо нову ще більшу матрицю. Невід’ємною особливістю добутку Кронекера також є й той факт, що його можна обчислювати для абсолютно будь-яких за розміром двох матриць
Наприклад, ми маємо такі дві матриці:
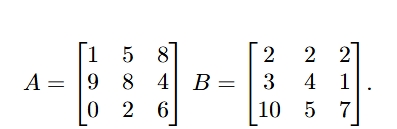
Ось приклад обчислення добутку Кронекера звичайним математичним записом:

Всі приклади з іншими матрицями обчислюються абсолютно таким самим чином. У нас завжди будуть матриці A та B, але різних розмірів. Тобто, якщо матриця A буде розміром 2×2, то кожен з чотирьох її елементів буде множитися на всю матрицю B.
Встановлення numpy
Windows:
pip install numpyMacOS:
pip3 install numpyLinux:
pip install numpyРеалізація у коді через функцію kron()
Для матриць 3×3
Спочатку імпортуємо бібліотеку numpy:
import numpy as npСтворюємо дві матриці a та b:
a = np.array(
[
[1, 5, 8],
[9, 8, 4],
[0, 2, 6]
]
)
b = np.array(
[
[2, 2, 2],
[3, 4, 1],
[10, 5, 7]
]
)У numpy добуток Кронекера реалізовується за допомогою функції kron(), якій ми передаємо у якості параметрів дві матриці будь-яких розмірів.
Тепер просто обчислюємо добуток Кронекера для наших матриць:
kronecker_product = np.kron(a, b)
print(f"Result:\n"
f"{kronecker_product}")Ось повний код нашої програми:
import numpy as np
a = np.array(
[
[1, 5, 8],
[9, 8, 4],
[0, 2, 6]
]
)
b = np.array(
[
[2, 2, 2],
[3, 4, 1],
[10, 5, 7]
]
)
kronecker_product = np.kron(a, b)
print(f"Result:\n"
f"{kronecker_product}")А ось отриманий результат:
Result:
[[ 2 2 2 10 10 10 16 16 16]
[ 3 4 1 15 20 5 24 32 8]
[10 5 7 50 25 35 80 40 56]
[18 18 18 16 16 16 8 8 8]
[27 36 9 24 32 8 12 16 4]
[90 45 63 80 40 56 40 20 28]
[ 0 0 0 4 4 4 12 12 12]
[ 0 0 0 6 8 2 18 24 6]
[ 0 0 0 20 10 14 60 30 42]]Ось ще один приклад:
import numpy as np
a = np.array(
[
[6, -10, 22],
[0, -35, 20],
[11, 47, 51]
]
)
b = np.array(
[
[-9, 0, 77],
[32, 41, -84],
[-10, 12, 62]
]
)
kronecker_product = np.kron(a, b)
print(f"Result:\n"
f"{kronecker_product}")Result:
[[ -54 0 462 90 0 -770 -198 0 1694]
[ 192 246 -504 -320 -410 840 704 902 -1848]
[ -60 72 372 100 -120 -620 -220 264 1364]
[ 0 0 0 315 0 -2695 -180 0 1540]
[ 0 0 0 -1120 -1435 2940 640 820 -1680]
[ 0 0 0 350 -420 -2170 -200 240 1240]
[ -99 0 847 -423 0 3619 -459 0 3927]
[ 352 451 -924 1504 1927 -3948 1632 2091 -4284]
[ -110 132 682 -470 564 2914 -510 612 3162]]Для матриць різних розмірів
Як вже було сказано на початку, добуток Кронекера можна обчислювати для матриць різних розмірів. Ось приклад, де ми маємо різні за розміром матриці, але все одно можемо обчислити добуток Кронекера:
import numpy as np
a = np.array(
[
[12, 0],
[8, 7],
[-2, -4],
[1, 9]
]
)
b = np.array(
[
[1, 5, 0, 10],
[12, 3, 2, 7],
[5, 8, 4, 3]
]
)
kronecker_product = np.kron(a, b)
print(f"Result:\n"
f"{kronecker_product}")Result:
[[ 12 60 0 120 0 0 0 0]
[144 36 24 84 0 0 0 0]
[ 60 96 48 36 0 0 0 0]
[ 8 40 0 80 7 35 0 70]
[ 96 24 16 56 84 21 14 49]
[ 40 64 32 24 35 56 28 21]
[ -2 -10 0 -20 -4 -20 0 -40]
[-24 -6 -4 -14 -48 -12 -8 -28]
[-10 -16 -8 -6 -20 -32 -16 -12]
[ 1 5 0 10 9 45 0 90]
[ 12 3 2 7 108 27 18 63]
[ 5 8 4 3 45 72 36 27]]Також ще один приклад:
import numpy as np
a = np.array(
[
[45],
[23],
[81]
]
)
b = np.array(
[
[53, -12],
[91, -34]
]
)
kronecker_product = np.kron(a, b)
print(f"Result:\n"
f"{kronecker_product}")Result:
[[ 2385 -540]
[ 4095 -1530]
[ 1219 -276]
[ 2093 -782]
[ 4293 -972]
[ 7371 -2754]]Висновок
У цій статті ми доволі просто й зрозуміло навчилися обчислювати добуток Кронекера у Python, користуючись бібліотекою numpy. Також важливим є й те, що ми розглянули й теоретичні задасади даного математичного прийому, що дало нам більше розуміння.
