
Як ми можемо побачити четвертий просторовий вимір? Річ у тім, що ніяк. Вищі виміри неможливо візуалізувати - марно навіть намагатися. МІЧІО КАЙКУ.
КОРОТКЕ ВСТУПНЕ СЛОВО.
Фізик Пейджелз Гайнц сказав наступну неймовірно правдиву фразу: “Одна властивість нашого фізичного світу настільки очевидна, що більшість людей над цим навіть не замислюється - те що простір тривимірний”. Дійсно, з тривимірністю ми постійно маємо справу в повсякденному житті, то ж сприймаємо її як даність. Підтвердженням цьому слугує той факт, що до сих пір жоден з науковців не намагався збудувати певний пристрій задля експериментальної перевірки розмірності простору.
Проте спробуємо відійти від звичного для нас 3D і поставимо питання як виглядає чотиривимірний світ та фігури в ньому. Спроби уявити це в голові з самого початку приречені на провал, оскільки людина - тривимірна істота з тривимірним мозком, а відтак і з тривимірним мисленням. Нам не під силу уявити чотири взаємно перпендикулярні прямі. [Навіть не намагайтеся це зробити. Викладачі фізичного факультету, на якому я вчився, говорили, що це шкідливо для психіки. :-) ]
Так невже не можливо хоч якось зрозуміти вищі виміри ? Насправді не все так погано як здається на перший погляд. Є один прийом, який дозволяє хоч і не побачити, але все ж таки опановувати та працювати з гіперпростором. Цей прийом - дуже потужний метод аналогій. Його суть можна подати у вигляді рецепту трьох послідовних дій. Перше: вивчення задачі у звичних та зрозумілих для нашого мозку дво- та тривимірному просторах. Друге: вбачання під час вивчення деякої закономірності. І нарешті третє: узагальнення поміченої закономірності на N-вимірний простір. Декому може здатися, що це годиться тільки для науково-популярної літератури і людей, які зовсім не розуміються в фізиці чи математиці, проте це помилкове судження. Метод аналогій дуже потужний, і ним користуються у своїх роздумах навіть науковці світового рівня.
У даному короткому нарисі я продемонструю застосування методу аналогій на трьох прикладах і спробую показати, що це зручний та сильний інструмент, який дозволяє проникати в загадки гіперпростору.
ПРИКЛАД 1. ТЕОРЕМА ПІФАГОРА.
Теорема Піфагора одна з самих древніх математичних теорем, яка була відома (у вигляді чисел Піфагора) ще в стародавньому Єгипті (~ 2000 роки до н. е.).
Для прямокутника на площині (тобто в 2D просторі) теорема формулюється наступним чином:
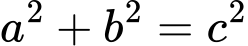
де a та b - довжини сторін прямокутника, c - довжина його діагоналі. Саме таке формулювання всі ми вчимо у школі на уроках геометрії.
На основі наведеної вище формули, легко довести, що для прямокутного паралелепіпеда справджується наступна рівність:
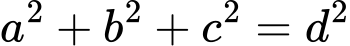
Ми тільки що записали тривимірне формулювання теореми Піфагора (a, b, c - позначають сторони прямокутного паралелепіпеда, d - його діагональ). Думаю, що тенденція зрозуміла: чим вищої розмірності прямокутний паралелепіпед будемо розглядати, тим більше доданків в лівій частині рівності з’являтиметься, причому їх кількість завжди співпадатиме з розмірністю простору, в якому ми працюємо. Овва, ви мабуть й самі не помітили як вже виконали другий пункт, описаного у вступному слові, рецепту. Тепер залишилося останній третій крок - узагальнити - який зробити дуже просто якщо правильно вловлено глобальну закономірність. Отже, теорема Піфагора в N-вимірному просторі запишеться в наступному вигляді:
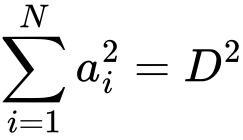
де N - розмірність простору, ai - позначення для і-ї сторони N-вимірного прямокутного паралелепіпеда, а D - довжина його діагоналі. Якщо сумніваєтеся в останній формулі, загляньте в будь-який підручник математики по цій темі і переконайтеся, що я не збрехав.
ПРИКЛАД 2. ЧУДО ГІПЕРСФЕРИ.
В школі ми дуже звикли до круга й шара (2D та 3D сфери). Проте в загальному випадку така фігура як “сфера” може мати будь-яку розмірність. В математиці є спеціальна назва для таких N-вимірних шарів - гіперсфера. Формально гіперсферу в просторі довільної розмірності означають як геометричне місце точок, рівновіддалених від заданої точки, яка є центром гіперсфери. (В принципі таке означення є цілком природнім. Згадайте звичайний круг: точки на колі рівновіддалені від центра круга.) Але перед тим як лізти у вищі розмірності, давайте трохи повивчаємо круг та шар і спробуємо вловити певну закономірність.
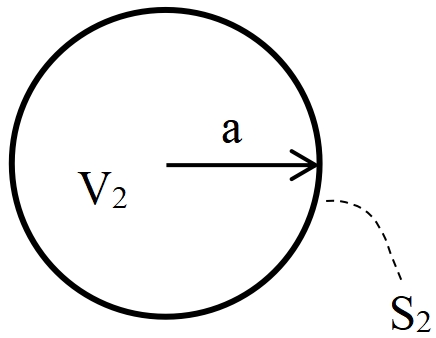
На рисунку вище зображено 2D сферу (круг) радіуса a. Довжину кола, що його обмежує (площа поверхні 2D сфери), позначимо S2, і запишемо вираз, який пов’язує довжину з радіусом кола:
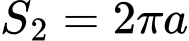
Схожу рівність можна записати для площі круга (об’єм 2D сфери), яку позначимо як V2:
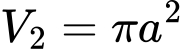
Якщо поділимо об’єм на площу, то одержимо наступне:
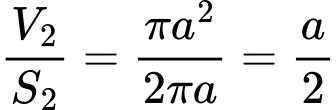
Пророблені викладки є елементарними, проте цікаво інше: ми працювали у двовимірному просторі, а в остаточному результаті в знаменнику дробу стоїть саме 2 (а не якесь інше число). Цікаво, а що ж “покажуть” такі самі обчислення для 3D сфери ? Давайте подивимось.
Площа поверхні шара S3 (тривимірний аналог S2) дається формулою:
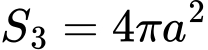
в той час як об’єм шара V3 (тривимірний аналог V2) пропорційний радіусу шара в третьому степені і обчислюється наступним чином:
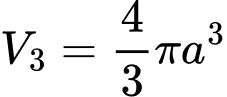
Як і в попередньому випадку, знайдемо відношення об’єму сфери до площі її поверхні. Отримаємо наступне:
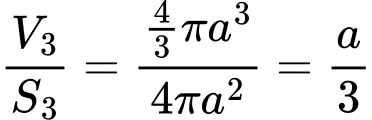
Бачимо, що одержано той самий факт: об’єм шару поділений на площу його поверхні рівний відношенню радіуса шара до розмірності простору (в даному випадку це число 3, оскільки шар - 3D сфера). Думаю, що закономірність ви вловили, і тому по аналогії до розглянутих вище випадків, можемо записати загальну формулу для відношення “об’єму” N-вимірної гіперсфери до “площі” її поверхні:
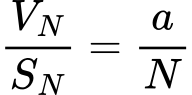
де а - радіус гіперсфери, N - розмірність простору. Сама остання формула абсолютно правильна. Її можна отримати строго, використовуючи явні вирази для V_N та S_N, але тут ми дійшли цього результату виключно за допомогою методу аналогій, не використовуючи складні математичні обчислення.
На цьому етапі вже можна дещо сказати відносно використовуваного нами методу. Звичайно, це не строге математичне доведення [прошу математиків зважати на те, що автор нарису - фізик :-) ], проте це дієвий спосіб, який дає правильний результат. Потужність методу аналогій полягає в тому, що він дає змогу ніби “обійти” ті самі строгі (і зазвичай складні) викладки. В результаті ми одержуємо деякий істинний факт без доведення, але знаючи істинність факту, знайти доведення це вже технічна справа, і тут я не буду “забирати хліб” у математиків.
На основі останньої формули можна дійти цікавого висновку, який я анонсував у назві розділу як “чудо гіперсфери”. Будемо збільшувати розмірність простору при незмінному радіусі сфери. Зрозуміло, що в цьому випадку, відношення V_N до S_N ставатиме все меншим (всилу того, що N стоїть в знаменнику). Математично це записується так:
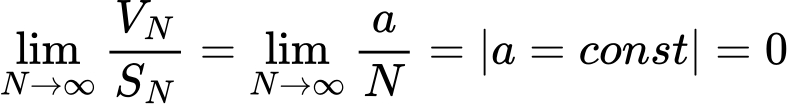
Остання формула означає, що чим більша вимірність простору, тим меншим стає об’єм гіперсфери порівняно з її площею. Це зовсім несподіваний результат(*), оскільки ми звикли до круга й шара, для яких об’єм це щось суттєво більше за площу поверхні.
(*)Фізичною мовою цей факт можна сформулювати так: у просторах високих розмірностей, поведінку фізичної системи визначають поверхневі явища, а не об’ємні.
ПРИКЛАД 3. ГЕОМЕТРІЯ КРОТОВИНИ.
Уявіть дві паралельні площини. Самі по собі вони є двовимірними об’єктами. Поки що нічого цікавого. А тепер уявіть, що в деякій точці верхньої площини починає формуватися ямка. Вона робиться все ширшою і тягнеться вниз до іншої площини. На нижній площині на зустріч ямці навпаки, виростає горбик. Десь посередині між паралельними площинами ямка та горбик зустрічаються та зливаються - між площинами утворився тунель. Утворена (і це вже 3D) структура буде виглядати наступним чином:
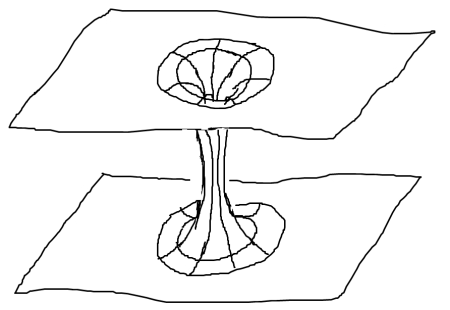
Такий тунель називається кротовиною. (Варто зазначити, що структура реальної кротовини набагато складніша, оскільки загальна теорія відносності оперує поняттям простір-час, стверджуючи, що простір та час є нерозривними між собою. Проте ми спростимо розгляд і зосередимося саме на просторовій геометрії кротовини, відкинувши час.)
Тут варто звернути увагу на кілька речей. По-перше, вхід в кротовину (так само як і вихід) має форму кола. По-друге, з самого початку ми мали двовимірні фігури (дві паралельні площини), а утворення ямки та горбика перетворили їх на тривимірну структуру. По-простому це можна сформулювати так: ямка в двовимірному просторі дає тривимірний простір. Це важливий факт, проте тут треба бути обережним. Це не тривимірний простір в повному розумінні.
Річ у тім, що для опису фігури зображеної на рисунку вище, достатньо базису з двох векторів (в цьому сенсі фігура все ж таки 2D). Полотно кротовини (поверхня тунелю) це все таки площина, якій надали хитромудрої форми, а оскільки координати будь-якого вектора на площині однозначно визначаються в двовимірному базисі, то те ж саме справедливо і для нашої кротовини. 2D корабель, що перелітав би між двома площинами за допомогою утвореного тунелю, рухався б по його 2D поверхні, а 2D пілот не помітив би нічого незвичного. Але з іншого боку, переміщаючись між площинами по тунелю, пілот навіть і не підозрював би, що рухається вздовж перпендикуляра до площин, тобто вздовж третьої осі тривимірного простору. Саме це я і мав на увазі коли сказав, що ямка в двовимірному просторі дає тривимірний простір.
Тепер ми маємо все, щоб зрозуміти геометрію реальної кротовини, яка може мати місце в нашому тривимірному світі. Варто тільки до сказаного вище застосувати метод аналогій.
По-перше, аналог кола в 3D просторі - це сфера. Отже, вхід (портал) реальної кротовини має форму сфери. Саме це і зображено у фільмі “Інтерстеллар”. Портал Гаргантюа є сферою і саме таким ми його і побачили, якби мали можливість долетіти, наприклад, до чорної діри в центрі нашої галактики Чумацький Шлях.
Другий момент стосується глобальної структури кротовини. По аналогії до двовимірного випадку можна сформулювати наступне: ямка в тривимірному просторі дає чотиривимірний простір(**). Але знову ж таки, як було сказано вище, це треба правильно розуміти.
Якби ми мали кротовину, що з’єднує одну частину нашої галактики з іншою, то поверхня такого тунелю була б тривимірна. Для опису такої поверхні в базисі повинно бути три вектори (цей факт залишає кротовину все таки 3D фігурою, а якщо точніше - реальна кротовина це насправді тривимірний простір, який хитромудро скручено в 4D структуру). 3D пілот, який мандрував кротовиною, спокійно летів би 3D світом і навіть не підозрював, що рухається вздовж четвертої осі чотиривимірного простору, осі, яка перпендикулярна одразу трьом взаємно перпендикулярним осям тривимірного Всесвіту, в якому ми живемо. Можливо від цього всього кружить голову, але так влаштована кротовина і таку ж геометрію (на мою особисту думку) мають чорні діри.
(**)Цей факт за допомогою методу аналогій можна узагальнити до такого формулювання: ямка в N-вимірному просторі дає (N+1)-вимірний простір.
КОРОТКА ПІСЛЯМОВА.
Ось і все. Три вищеописані приклади наглядно демонструють застосування методу аналогій. Ми змогли обійти складні математичні викладки та обчислення (наприклад, ми не виводили точні вирази для об’єму чи площі поверхні гіперсфери, не розв’язували рівнянь загальної теорії відносності для кротовини), але не дивлячись на це, всюди одержали правильні відповіді.
Цікаво також те, що ми працювали з гіперпростором, не уявляючи при цьому в голові вищих вимірів. Ми не ламали голову над питанням як виглядає N-вимірний прямокутний паралелепіпед, але це не завадило нам записати теорему Піфагора для нього. Ми не уявляли гіперсферу, проте знайшли відношення її об’єму до площі поверхні. Ми гадки не мали (і не маємо) як виглядають чотири взаємно перпендикулярні прямі, але змогли зрозуміти геометрію кротовини та чорних дір. І це все використовуючи тільки метод аналогій.
Користуйтеся ним і зможете описувати і працювати з багатовимірними фігурами, формулювати математичні теореми для N-вимірних світів та проникати в загадки гіперпростору.
