У цій статті ми будемо займатися символьним обчисленням інтегралів у Python за допомогою спеціальної бібліотеки sympy. Ми будемо обчислювати усі наявні види інтегралів.
Встановлення
Для Windows:
pip install sympyДля MacOS:
pip3 install sympyДля Linux:
pip install sympyКласичні інтеграли
Спочатку пропоную розглянути символьне обчислення доволі звичайних інтегралів — визначених та невизначених.
Невизначені інтеграли
Отже, невизначені інтеграли — це такий ти інтегралів, який не має меж. Пропоную спробувати записати ось такий інтеграл у рамках цього розділу статті:
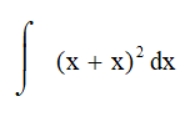
Спершу імпортуємо бібліотеку sympy, яка надає можливість проводити обчислення символьно:
import sympy as spДалі створимо функцію, яка буде приймати потрібні параметри та інтегрувати:
def indefinite_integral(function, x):
integration = sp.integrate(function, x)
print(f"Result: {integration}")Наступним кроком стврюємо так звану символьну змінну, яку будемо інтегрувати:
x = sp.Symbol("x")Тепер сворюємо змінну для нашої підінтегральної функції:
function = (x + x) ** 2Ось повний код:
import sympy as sp
def indefinite_integral(function, x):
integration = sp.integrate(function, x)
print(f"Result: {integration}")
x = sp.Symbol("x")
function = (x + x) ** 2
indefinite_integral(function, x)Тепер запускаємо код і бачимо настпуний результат:
Result: 4*x**3/3Визначені інтеграли
Визначені інтеграли на відміну від невизначеих мають межі інтегрування. У рамках цього розділу запишемо цей інтеграл:
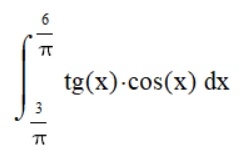
Для запису цього інтеграла створюємо функцію для обчислення саме визначених інтегралів. Ось який вона буде мати вигляд:
def definite_integral(function, x, lower_limit, upper_limit):
integration = sp.integrate(function, (x, lower_limit, upper_limit))
print(f"Result: {integration}")Тут після змінної інтегрування ми ще додали lower_limit та upper_limit — нижня та верхя межа нашого інтеграла.
Визначаємо наші межі у відповідних змінних:
lower_limit = 3 / sp.pi
upper_limit = 6 / sp.piЗмінюємо підінтегральну функцію:
function = sp.tan(x) * sp.cos(x)Все інше залишаємо як і було. Повний код для обчислення визначеного інтеграла виходить таким:
def definite_integral(function, x, lower_limit, upper_limit):
integration = sp.integrate(function, (x, lower_limit, upper_limit))
print(f"Result: {integration}")
x = sp.Symbol("x")
function = sp.tan(x) * sp.cos(x)
lower_limit = 3 / sp.pi
upper_limit = 6 / sp.pi
definite_integral(function, x, lower_limit, upper_limit)Отримуємо такий результат обчислення:
Result: -cos(6/pi) + cos(3/pi)Невласні інтеграли
Невласні інтеграли — це такий вид інтегралів, у яких одна або усі межі є нескінченність. Вони поділяються на два невласні інтеграли 1-го роду та невласні інтеграли 2-го роду.
Невласні інтеграли 1-го роду
Невласні інтеграли 1-роду вирізняються тим, що вони мають в одній або усіх своїм межах саме знак нескінченності.
За приклад візьмемо отакий інтеграл:
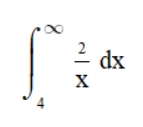
По суті єдине, що ми змінюємо з поперднього коду це підінтегральну функцію та межі. Робимо зміни:
function = 2 / x
lower_limit = 4
upper_limit = sp.ooПримітка. У sympy нескінченність позначається як оо. Тому sp.oo — це позначення нескінченності.
Повний код виходить таким:
def improper_integral_first_kind(function, x, lower_limit, upper_limit):
integration = sp.integrate(function, (x, lower_limit, upper_limit))
print(f"Result: {integration}")
x = sp.Symbol("x")
function = 2 / x
lower_limit = 4
upper_limit = sp.oo
improper_integral_first_kind(function, x, lower_limit, upper_limit)Отримуємо результат:
Result: ooНевласні інтеграли 2-го роду
Невласні інтеграли 2-роду — це такі такий тип інтегралів, у яких немає нескінченностей у межах, але нескінченність утворюється у підінтегральному виразі.
Спробуємо обчислити такий інтеграл:
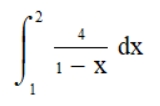
Тут ми бачимо вираз 1 — x у знаменнику — це якраз і є той момент, коли ми отримуємо нескінченність у підінтегральній функції. Так як коли змінна x = 1, то вираз 1 — 1 = 0. Виходить, що ми ділимо на нуль, а при діленні на нуль ми отримуємо нескінченність.
Знову змінюємо межі та підінтегральну функцію. Одразу можна показати повний код:
def improper_integral_second_kind(function, x, lower_limit, upper_limit):
integration = sp.integrate(function, (x, lower_limit, upper_limit))
print(f"Result: {integration}")
x = sp.Symbol("x")
function = 4 / (1 - x)
lower_limit = 1
upper_limit = 2
improper_integral_second_kind(function, x, lower_limit, upper_limit)Результат:
Result: -ooКратні інтеграли
Кратними називаються подвійні та потрійні інтеграли. У цих видах інтегралах ми інтегруємо одразу по двом чи трьом змінним. Відповідно знаків інтеграла буде два або три.
Подвійні інтеграли
Подвійні інтеграли дозволяють інтегрувати одразу по двома змінним. Це ми можемо побачити у цьому прикладі:
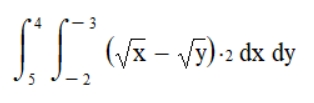
Отже, додаємо нову символьну змінну — y:
y = sp.Symbol("x")Записуємо нову підінтегральну функцію:
function = (sp.sqrt(x) - sp.sqrt(y)) * 2Визначаємо межі для x та y:
lower_limit_x = 5
upper_limit_x = 4
lower_limit_y = -2
upper_limit_y = -3Тепер наша функція буде приймати більше параметрів, ось повний код програми:
def double_integral(function, x, lower_limit_x, upper_limit_x, y, lower_limit_y, upper_limit_y):
integration = sp.integrate(function, (x, lower_limit_x, upper_limit_x), (y, lower_limit_y, upper_limit_y))
print(f"Result: {integration}")
x = sp.Symbol("x")
y = sp.Symbol("y")
function = (sp.sqrt(x) - sp.sqrt(y)) * 2
lower_limit_x = 5
upper_limit_x = 4
lower_limit_y = -2
upper_limit_y = -3
double_integral(function, x, lower_limit_x, upper_limit_x, y, lower_limit_y, upper_limit_y)Результат:
Result: -32/3 + 20*sqrt(5)/3 - 4*sqrt(3)*I + 8*sqrt(2)*I/3Потрійні інтеграли
Останніми у статті будуть потрійні інтеграли. Сенс в принципі той самий, що й з подвійними, тільки у потрійних ми маємо справу з трьома змінними та трьома занаками інтеграла. Тобто ми інтегруємо по трьом змінним.
Пропоную обчислити такий потрійний інтеграл:
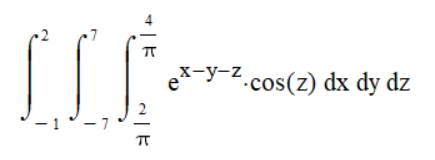
Знову-таки змінюємо межі, підінтегральну функцію і додаємо нову символьну змінну z:
def triple_integral(function, x, lower_limit_x, upper_limit_x, y, lower_limit_y, upper_limit_y, z,
lower_limit_z, upper_limit_z):
integration = sp.integrate(function, (x, lower_limit_x, upper_limit_x), (y, lower_limit_y, upper_limit_y),
(z, lower_limit_z, upper_limit_z))
print(f"Result: {integration}")
x = sp.Symbol("x")
y = sp.Symbol("y")
z = sp.Symbol("z")
function = sp.exp(x - y - z) * sp.cos(z)
lower_limit_x = -1
upper_limit_x = 2
lower_limit_y = -7
upper_limit_y = -7
lower_limit_z = 4 / sp.pi
upper_limit_z = 2 / sp.pi
triple_integral(function, x, lower_limit_x, upper_limit_x, y, lower_limit_y, upper_limit_y, z,
lower_limit_z, upper_limit_z)Результат:
Result: 0Висновок
У даній статті ми навчиися інтегрувати інтеграли різних видів за допомогою бібіліотеки для символьних розрахунків sympy. Також дещо розібрали особливість кожного інтеграла і навчилися реалізовувати їх у коді. Всім дякую за увагу!
