Леонард Ойлер - напевне найбільш видатний математик взагалі, і точно найбільш видатний математик XVIII сторіччя. Він написав близько 850 наукових робіт, винайшов декілька розділів математики, вніс вклад в астрономію, механіку, гідродинаміку, оптику, що тільки не. Його перу належить формула, яка вважається найкрасивішою і найелегантнішою в математиці. Якщо перекласти кількість його робіт в час, то він робив наукове відкриття приблизно раз на тиждень.
І, очевидно, Ойлер був дуже занятою людиною. Тому, я думаю, мер Данціга не очікував на відповідь, коли надсилав йому листа - звичайно, у XVIII сторіччі комунікація відбувалася переважно листуваннями. Питання мера Данціга здалося Ойлеру тривіальним, але, тим не менше, викликало потужний інтерес, настільки, що з міркувань щодо цього питання народився новий розділ математики, який ми зараз використовуємо де тільки не. Наведу тут цитату з листа-відповіді Ойлера у вільному перекладі:
…. тому, бачите, шановний пане, наскільки цей тип розв’язання мало пов’язаний з математикою, і я не розумію, чому ви очікуєте, що математик це розв’язання зробить краще ніж будь-хто інший, оскільки розв’язання базоване тільки на міркуваннях, і його відкриття не залежить ні від якого математичного принципу. Тому я не знаю чому навіть питання які мають настільки мало зв’язку з математикою розв’язуються математиками швидше, ніж будь-ким іншим.
Ох, Ойлер, my sweet summer child.
У листі до італійського математика Джованні Маріноні Ойлер написав:
Це питання настільки банальне, але воно здалося мені гідним моєї уваги, оскільки ні геометрія, ні алгебра, ні навіть мистецство рахування не було достатнім щоб розв’язати його.
Спойлер: приблизно так і народжуються нові розділи науки.
А питання було наступне:
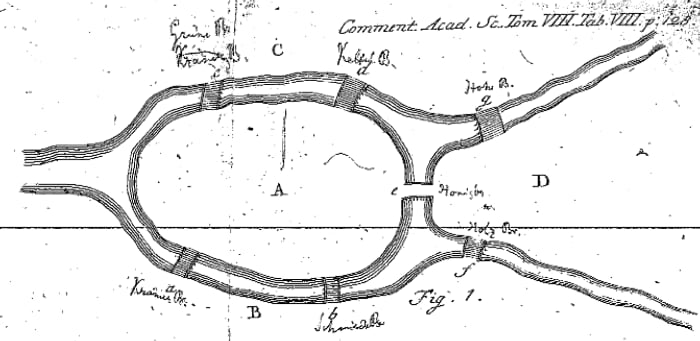
Подивіться уважно на малюнок. На ньому схематично зображена мапа міста Кенігсберг, з річкою, двома островами у річці і сім’ю мостами. Чи можна зробити прогулянку містом таким чином, щоб пройти по кожному мосту рівно один раз?
Це неможливо розв’язати ніякими методами геометрії, відомої сучасникам Ойлера. Потрібна була якась нова геометрія - геометрія позиції - як назвав її Готфрід Ляйбніц (один з татусів математичного аналізу). Зараз ми називаємо геометрію позицій теорією графів, і це хіба не найприкладніша математика у світі, тому що її приклали до всього що тільки можна, навіть до лінгвістики і соціології.
Отже, давайте думати.
Спочатку позбудемося всіх речей, які відволікають увагу. На що ми справді дивимося?
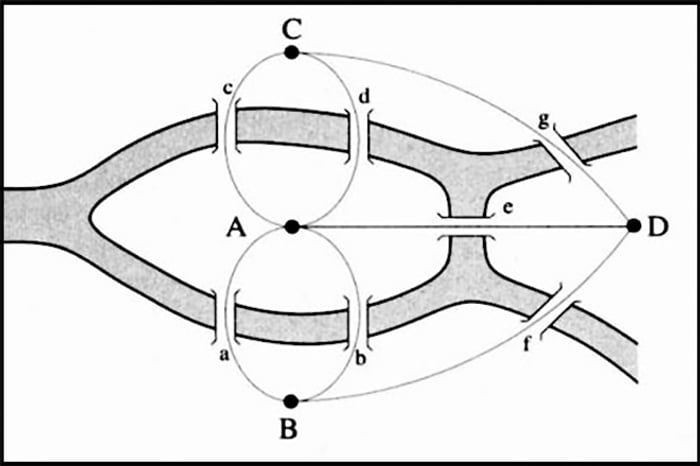
Розміри островів і берегів не мають значення, який шлях на островах і берегах теж значення не має - сплющимо їх до точок, або вершин. Лінійні розміри мостів також не мають значення - замінимо їх лініями, які сполучають точки. Назвемо ці лінії ребрами. Це інноваційний спосіб дивитися на речі, якщо ви математик у XVIII сторіччі.
Якщо тепер відкинути мапу повністю, отримаємо малюнок справа. Знайомтеся: граф.

Тепер ще раз подивимося на наше питання і усвідомимо, що насправді нам потрібно просто розставити стрілочки на всіх ребрах таким чином, щоб кожне ребро проходилося рівно один раз.
А якщо кожне ребро проходиться рівно один раз, то що нам це каже про вершини? Що в кожну вершину потрібно дійти, а потім з неї вийти - тобто кількість ребер, виходячих з вершини має бути парною (якщо шлях замкнений), або має бути вершина-початок і вершина-кінець, які мають по непарній кількості ребер (початок шляху і кінець шляху, якщо вони не співпадають), а всі інші - знову-таки мати парну кількість ребер.
На нашому графі кожна з чотирьох вершин має непарну кількість ребер. Отже, необхідний нам шлях (який тепер називається Ойлерівським шляхом) - неможливий. Катастрофа для теоретичної прогулянки Кенігсбергом, велика перемога для математики.
