
В математиці (і загалом в науці) гарно працює принцип Арнольда:
Якщо об’єкт/теорема/лема названа іменем людини, значить відкрила цей об’єкт/теорему/лему НЕ ця людина.
Це стосується і стрічки Мебіуса. Хоча Мебіус і Лістінг незалежно один від одного відкрили цей об’єкт у 1858 році, вперше він з’являється ще на римських мозаїках III сторіччя (хоча існує думка, що це могло бути випадково).
Візьміть смужку паперу та склейте її кінцями. Ви отримаєте порожній циліндр - і, якщо ви оберете сторону, і почнете малювати олівцем лінію “просто вперед“, то рано чи пізно ви зустрінете місце, з якого ви почали. Інша сторона, при цьому, залишиться порожньою. У об’єкта по імені “циліндр“, значить, дві сторони: зовнішня і внутрішня.
Тепер візьміть іншу стрічку. І також склейте її, але на цей раз - так, щоб стрілочки на малюнку співпадали.

І проведіть той самий експеримент: ручка, лінія… Ні, чесно, прямо зараз візьміть і проведіть, ми тут без спойлерів, а ще це просто потрібно побачити своїма очима - інакше хіба ви мені повірите?
Ви можете помітити в процесі, що щось малювання лінії на такому об’єкті довше, ніж на циліндрі. Воно і не дивно: якщо тепер ви розріжете місце, де спочатку склеїли, і розгорнете стрічку, то побачите, що взагалі-то тепер ваша лінія намальована на обох сторонах. Тобто до розрізання у нас був об’єкт з одною стороною.
Ну, до речі, знайомтеся: Стрічка Мебіуса. В якийсь момент механіки додумалися використовувати її замість звичайної пасової передачі, тому що таким чином вона зношується в два рази повільніше - бо взаємодіє з валом не одна сторона “циліндру“ смужки, а вдвічі більша єдина сторона стрічки Мебіуса.

Але на цьому наші відкриття не закінчуються! Давайте посадимо на стрічку Мебіуса вектор - намалюйте стрілочку паралельно місцю, де ви склеювали стрічку. Тепер копіюйте цю стрілочку кожні пару міліметрів вправо, доки не дійдете до першої стрілочки, яку ви намалювали. Що ви бачите?

Або подивіться уважно на цю гіфку:
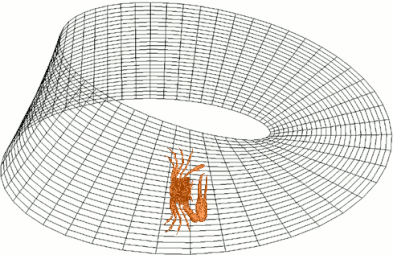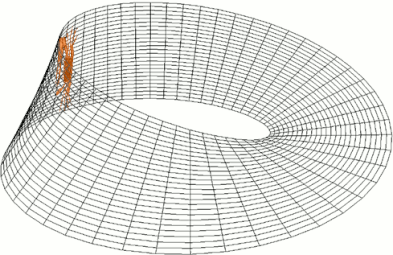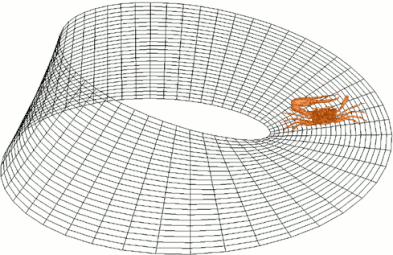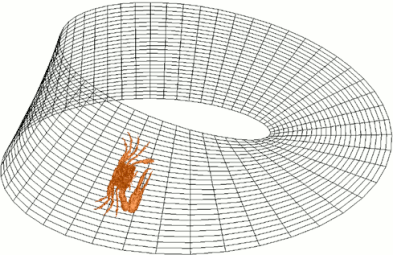
Ми бачимо відсутність так званої орієнтації (не тієї, а математичної). Якщо б ми жили на стрічці Мебіуса, то в нас не було б годинників - ми буквально не вміли б розрізняти “за годинниковою стрілкою“ і “проти годинникової стрілки“, точніше, в різних місцевостях це були б різні речі. Не було би консистентного визначення.
На щастя, ми живемо на сфероподібній поверхні (штуки розмірності два), вони орієнтовні. Взагалі, всі орієнтовні (+замкнені і зв’язні) двовимірні поверхні вже давно прокласифікували, і виглядає ця класифікація приблизно так:
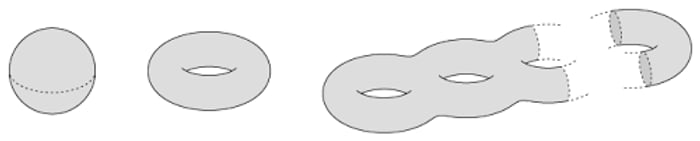
Штука з нулем дірок називається сферою. Штука з однією діркою називається тором. Штука з двома дірками називається 2-тором, трьома - 3-тором, і так далі. 2-тор можна отримати з двох звичайних торів процедурою зв’язної суми, яка виглядає так:
А щоб прокласифікувати взагалі всі двовимірні зв’язні замкнені поверхні, нам потрібно зі стрічки Мебіуса зробити так званий кросс-кап, щоб вклеювати його в поверхні.
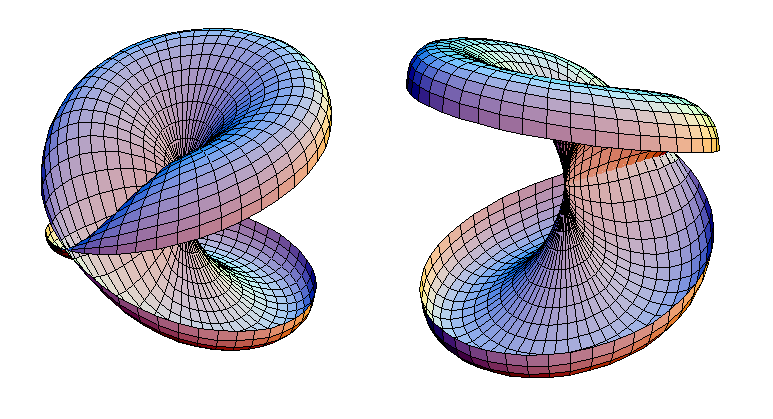
Для того щоб розібратися з твердженням теореми про класифікацію поверхонь нам залишилося розібратися лише з гомеоморфізмами.
Взагалі, ми зараз знаходимося у світі топології. В цьому конкретному довгочиті, я маю на увазі. Топологія - це що можна отримати з геометрії, якщо тепер всі наші об’єкти будуть з гуми. Тобто, ми дозволяємо будь-які неперервні деформації, і все що не розриває гуму - дозволене. І ще ми називаємо такі деформації гомеоморфізмами.
Наприклад, якщо у нас є гумове кілечко, його можна сплюснути в квадрат. Топологія вважає ці об’єкти однаковими. Сферу можна розтягнути в куб - теж однакові об’єкти. Ось, наприклад, ілюстрація топологічної еквівалетності чашки і тора:

Отже, ми готові прокласифікувати всі зв’язні замкнені поверхні!
Будь-яка замкнена зв’язна поверхня гомеоморфна до однієї з наступних поверхонь: сфери, скінченної зв’язної суми торів, або сфери з вирізаною скінченною кількістю дисків, які замінили на кросс-капи.
З цих товаришів сфера і тори - орієнтовні, а сфера з вклеєними кросс-капами - неорієнтовна.
Але кросс-кап - це просто зклейка стрічки Мебіуса! Отже, буквально виходить так, що якщо якась двовимірна поверхня неорієнтовна, це починається зі стрічки Мебіуса.
Перші кроки до класифікаційної теореми (математики люблять класифікувати) зробив ще сам Мебіус у 1870, але по-чесному це довели Ден і Хеєгард у 1907 (топологія - молода наука), за умови що поверхні можна тріангулювати (замостити трикутниками). А те, що їх можна тріангулювати довів вже Радо у 1925 році. Більше 55 років - тільки на класифікацію!
