Евклід
Як не дивно, почнемо ми цю історію з Евкліда з Александрії, а точніше, його аксіоматики геометрії, вперше описаної в монументальних тринадцяти книгах, названих “Начала“ або “Елементи“.
Якщо думати про математику як про гру, то аксіоматика - це правила гри, з яких ми стартуємо. Вона не пояснюється, її не можна вивести, вона просто дана. Ми не можемо дати визначення точці, тому ми просто приймаємо, що точки існують - і вже продовжуємо від цього.
Аксіоматика геометрії, запропонована в “Началах“, має п’ять аксіом. Давайте подивимося на них.
1. Від усякої точки до всякої точки можна провести пряму лінію.
2. Обмежену лінію можна безперервно продовжувати до прямої.
3. З усякого центра довільним розхилом циркуля може бути описане коло.
4. Усі прямі кути рівні між собою.
5. Якщо пряма, що перетинає дві прямі, утворює внутрішні односторонні кути, які менші ніж два прямі кути, то ці дві прямі, продовжені необмежено, зустрінуться з тієї сторони, де кути менші за два прямі.
Нас буде цікавити п’ята аксіома - її ще називають аксіомою паралельності. Буквально можна переформулювати як “паралельні прямі не перетинаються“.
Аксіоматика Евкліда, до речі, не є логічно повною, тому у XX сторіччі Гільберт запропонував розширену аксіоматику пласкої геометрії, про яку чудовий польський математик Тарський довів, що вона вже є повною. Про Тарського ми ще поговоримо, але в іншому довгочиті.
Інтерлюдія: Платон, Архімед, Пенроуз.
Є така штука - паркет. В математиці теж існує паркет, і він навіть приблизно те саме робить. Паркетом ми застилаємо підлогу і паркет періодичний (ми беремо однакові шматочки дерева і контрл+ц контрл+в). Тільки зазвичай математики називають паркет теселяцією.
Які властивості має теселяція? Це многокутники, які мають або спільну сторону, або спільну точку, або не мають спільного нічого. Між ними немає проміжків. Вони мають повторюватися таким чином, щоб ними можна було заповнити весь простір.
Інтерлюдія в інтерлюдії: існував такий давньогрецький філософ і натуральний філософ Платон. Він дуже любив правильні многогранники, і навіть писав про них в своїх Діалогах - кожне платонове тіло відповідало якійсь стихії. Правильні, симетричні штуки - дуже популярна в математиків тема, тому що ми любимо красиве. Оскільки офіційного розділу на науки в давньогреків не існувало, всі займалися всім, тож філософія і математика існували поряд і всіх все влаштовувало. Евклід писав про Платонові тіла в Елементах. Йоганнес Кеплер намагався побудувати модель Сонячної системи, використовуючи Платонові тіла. Серйозно, дуже популярна штука.

Так ось, Платон полюбляв правильні многогранники. Тому три перших теселяції - теселяції правильними многокутниками - названі Платоновими.

Напівправильні теселяції - вони складаються з двох або більше різних многокутників - отримали ім’я Архімеда.
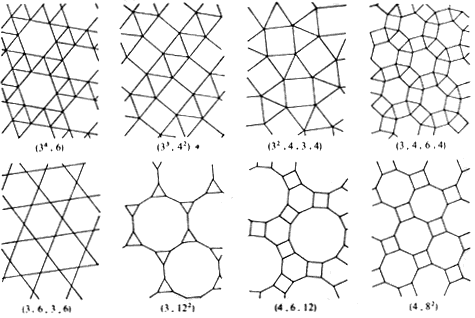
Теселяції - це взагалі дуже весела тема, про яку можна говорити нескінченно, але сьогодні нас цікавлять тільки основні поняття.
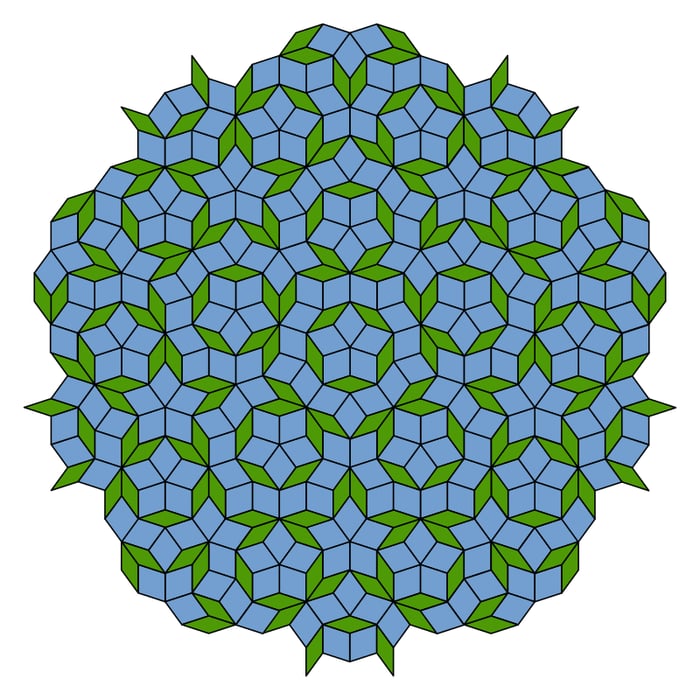
Але, все-таки, не утримаюсь і покажу вам мозаїку Пенроуза. Коли математики розібралися з періодичними теселяціями (і це має відношення до кристалографії, як не дивно), вони почали цікавитися аперіодичними теселяціями. Ось одна з них, вперше опублікована в 1978 році Роджером Пенроузом.
І все-таки, де Ешер?
Моріц Ешер був зацікавлений в симетрії. Взагалі, якщо мене не підводить пам’ять, Моріц Ешер розпочинав як архітектор - і це багацько пояснює в його творчості, але не все. Я не буду розповідати вам його біографію, тому що сама не спеціалістка, зате я дуже люблю дивитися на його картини. І, як ви думаєте, що там можна побачити?

Три геометрії
У математиків є чудова традиція: дивитися на аксіоми і думати, чи можна їх кількість якось зменшити. Тобто, чи являються ці аксіоми справді аксіомами, чи вони все-таки теореми, які можна вивести з інших аксіом? Ось якось в такому процесі у XIX сторіччі Михайло Лобачевський виявив, що насправді без п’ятої аксіоми цілком можна жити. Просто виходять інші геометрії. Ось там в цитаті зверху я написала про Гільберта і аксіоматику пласкої геометрії. І справді, в школі ми вивчаємо саме пласку геометрію - спочатку на площині (планіметрію), потім у просторі (стереометрію).
Але ми живемо на достатньо кулеподібному камені в космосі. У нього є якась кривизна. Ніколи не задумувалися, чому літаки літають не по “пласким“ прямим, а по дугам?
Якщо довго над цим думати, можна придумати сферичну геометрію, де п’ятий постулат Евкліда не виконується. Якщо ми тепер будемо думати про пряму як про коло, яке знаходиться на поверхні сфери і ділить її на дві рівні половини - то паралельних прямих не існує.
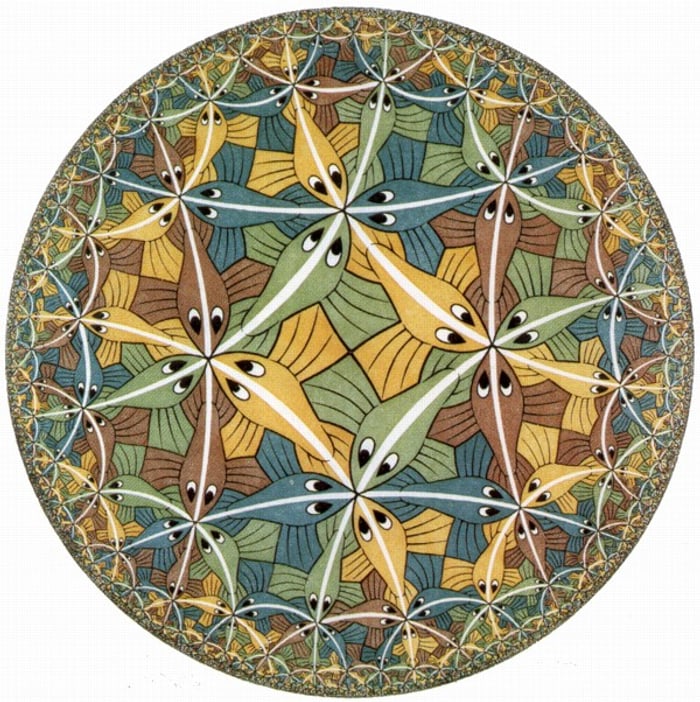
А от теселяції сфери - існують. І Ешер це робив.

А потім з’явився Коксетер
Попередній розділ названо “три геометрії“, але там є тільки пласка і сферична. Це дві. Яка третя?
Давайте подумаємо: поки що ми були в ситуації, коли паралельних прямих взагалі не існує, або тільки одна (через задану точну). А чи може їх бути безліч?
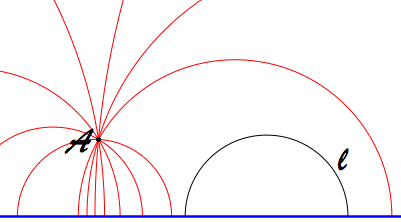
Цю геометрію - гіперболічну геометрію - і відкрив Лобачевський.
І саме цю геометрію відкрив Ешеру Коксетер.
Якщо пласка геометрія має відношення до кривизни нуль, то сферична - до додатньої кривизни, а гіперболічна - від’ємної. Сфера опукла, гіперболічний простір - навпаки.
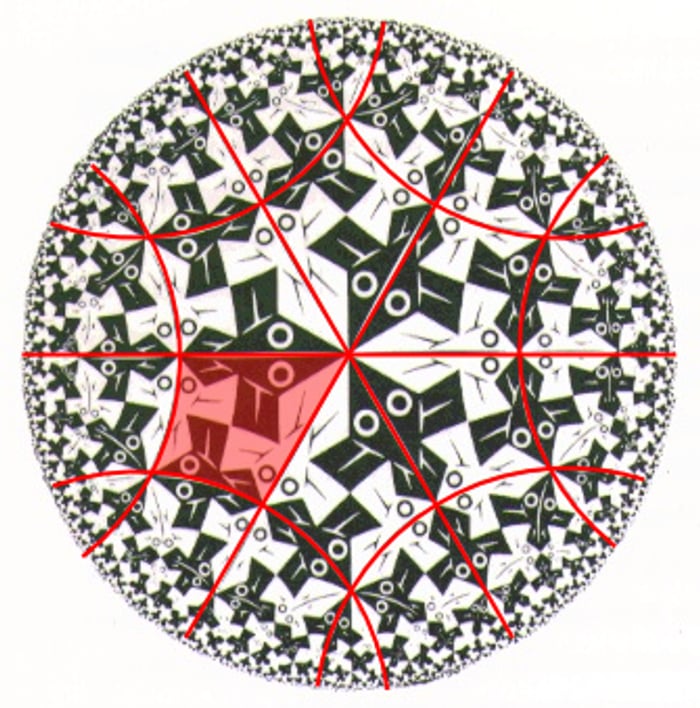
І справді, якщо сфера для нас інтуітивно зрозуміла (складніше, звичайно, ніж щось пласке, але уявити в принципі можна), то гіперболічний простір не дуже зрозуміло навіть звідки починати уявляти. Тому математики оперують моделями гіперболічного простору, в кожній з яких комфортніше бачити якісь конкретні явища.
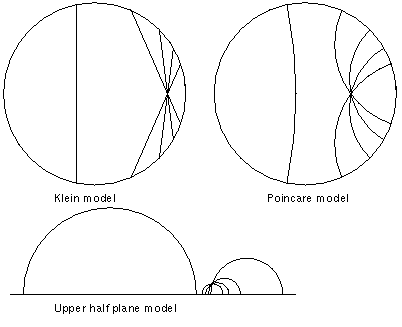
Про це я теж вам якось розповім, але зараз мова про те, що просто отак взяти і намалювати гіперболічний простір не так вже й легко. Тому Коксетер не просто знайомий математик Ешера, Коксетер - головна рушійна сила в цілій епосі творчості Ешера.
Як це сталося? Був великий математичний конгрес, Коксетер на ньому робив доповідь про теселяції, а у Ешера на той момент вже була видана книжка дизайнів теселяцій Евклідової (пласкої) площини. Коксетер написав Ешеру лист і спитав, чи можна якісь дизайни використати в доповіді, Ешер погодився, і перед доповіддю на конгресі Коксетер надіслав Ешеру текст подивитися. Там Ешер побачив регулярну теселяцію гіперболічної площини в моделі Пуанкаре. І понеслося.

Circle Limit series
Тепер, мені здається, ви можете в повній мірі насолодитися красою цих картин - і красою того шляху, який цим картинам передував.