Основна складність у розв’язанні інтегралів полягає у плутанині великої кількості технік інтегрування. У цій статті я детально розповім про суть інтегралів та систематизацію техніки інтегрування. З цим, розв’язання навіть складного інтеграла можна зробити у декілька строк.
В чому суть математики?
Це питання починає назрівати в голові вже після років вивчення математики, але, як на мене, відповідь на нього є першим кроком до розуміння інтегралів насправді.
Математика дає інструменти для оцінки того, що і так здається логічним. Вона не змушує “висасувати з пальця” теорії, які можна віднести до фантастики. Ви можете самостійно вивести формулу площі кола, граючись з кількістю розрізів та товщиною цих розрізів. Математика - це спосіб доведення фундаментальних та складних принципів через те, що вас оточує. Майже всі складні теореми були доведені через розбиття на складові частини та їх подальшу суму.
Повернімося до прикладу з площею кола, цей приклад детально показаний у серії відео 3Blue1Brown.
Маємо найзвичайнісіньке коло з радіусом R = 3.

Площу кола можна знайти через суму розрізів кола (уявіть як ріжете торт), але для цього треба “розрізати” коло на такі частинки, щоб можна було знайти площу цих розрізів.
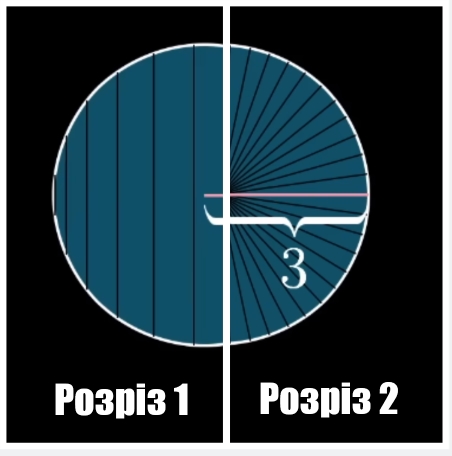
Варіанти розрізів Жоден з варіантів розрізів не підходить, чому б не спробувати розріз по кільцям, як у стовбура дерева?

Розріз по кільцям Спробуємо знайти площу кожного кільця, або вивести формулу для знаходження. Припустимо, що якщо “розкрити” кільце вийде прямокутник, формулу якого вже маємо.
Ширину утвореного прямокутника можна знайти по формулі довжини кола, бо, задля простоти експерименту, вона нею і буде.
Висоту прямокутника, товщину зрізу, задамо константою 0.1 (це може бути як велике, так і маленьке число, задля спрощення обчислень, нехай буде маленьке число).
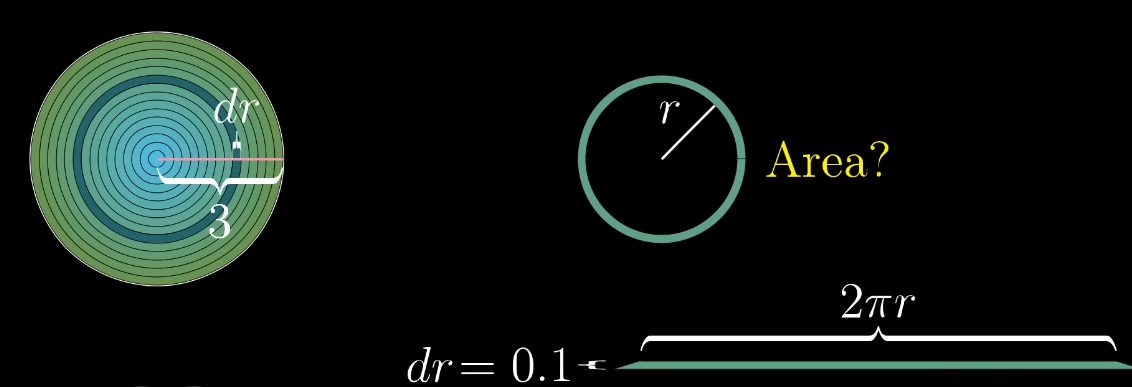
Площа розрізу Тепер, маючи ширину та довжину прямокутника, знаходимо площу за формулою: 2rdr.
Маючи щойно створену формулу, розраховуємо площу кожного розрізу, після чого сумуємо площі всіх розрізів. Прекрасно! Але наскільки точне таке обчислення? Як бачимо, наше коло складається з 15 розрізів, але через велику товщину кожного розрізу, між ними є пространство, через що коло виглядає не дуже правдоподібно.
Зменшуючи товщину кола, наприклад, до dr = 0.00001, розрізи розташовані щільніше, коло вже набуває правильної форми. Але тепер потрібно знаходити площу більшої кількості розрізів.

Зменшуючи товщину, розрізи зливаються один з одним Спробуємо знайти швидший спосіб.
Спершу спробуємо знову “розкрити” кожен розріз і розташувати його на координатній площині, від найменшого до найбільшого. Дивлячись уважно можна побачити, що зменшуючи товщину розрізу ще більше, dr = 0.000000000000001, маємо майже цільний трикутник, тож тепер площа кола - це площа під прямою, “гіпотенузою” трикутника, тобто - площа трикутника.
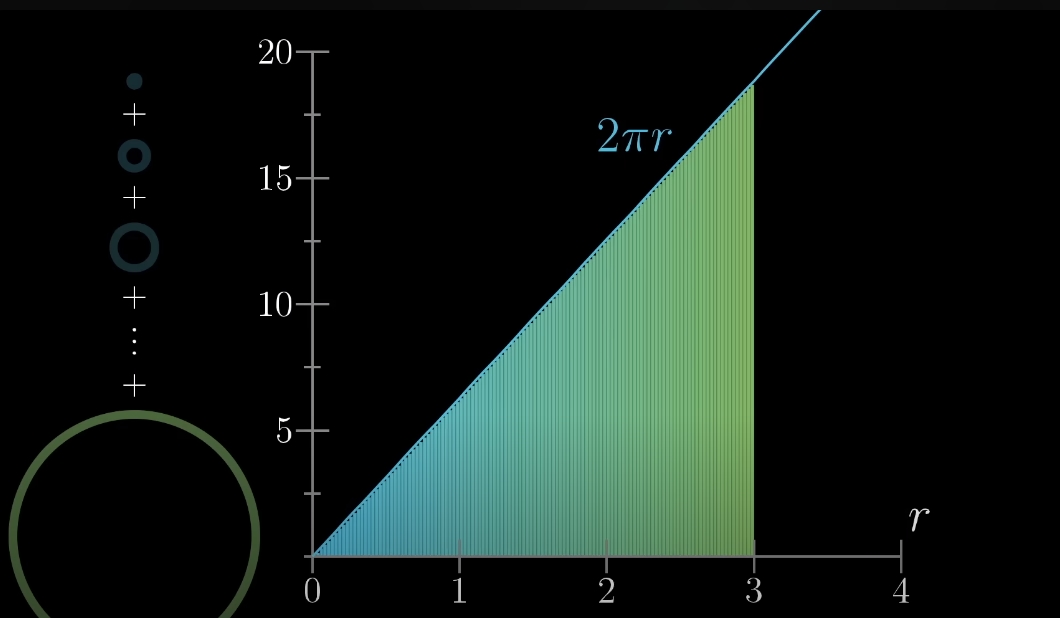
Утворений трикутник Розрізи утворюють прямокутний трикутник, з висотою кожного розрізу 2r (поставимо кожен прямокутник так, щоб довжина стала висотою)
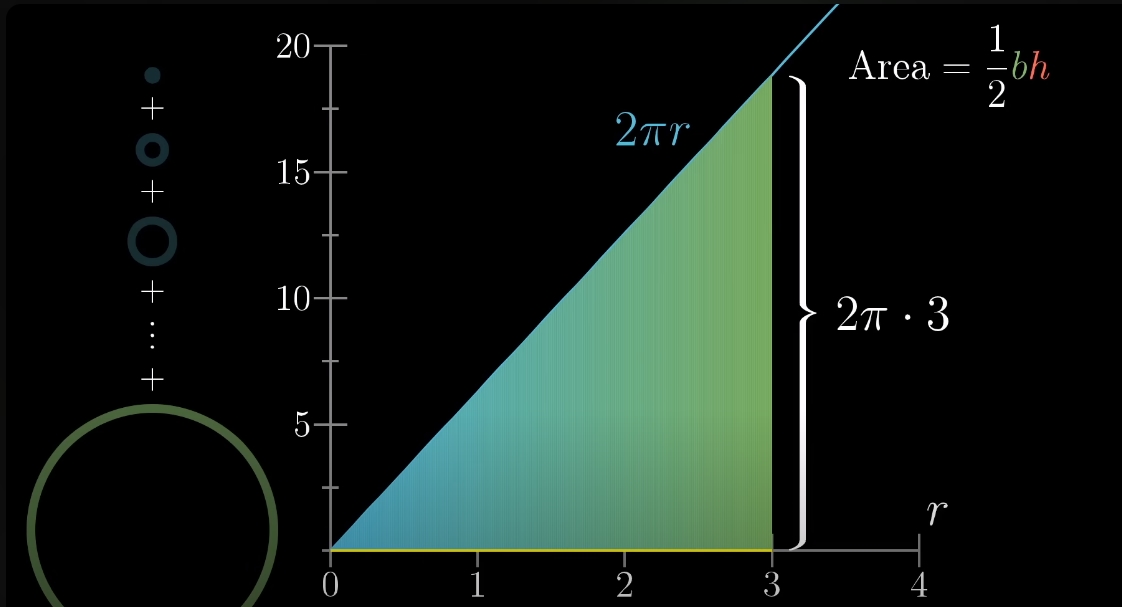
Основа прямокутного трикутника дорівнює радіусу, 3, тоді як бічна сторона - це довжина розрізу, тобто 2r. R для найбільшого розрізу дорівнює радіусу кола, 3, бічна сторона буде 6.
Обчислюємо площу прямокутного трикутника за формулою.
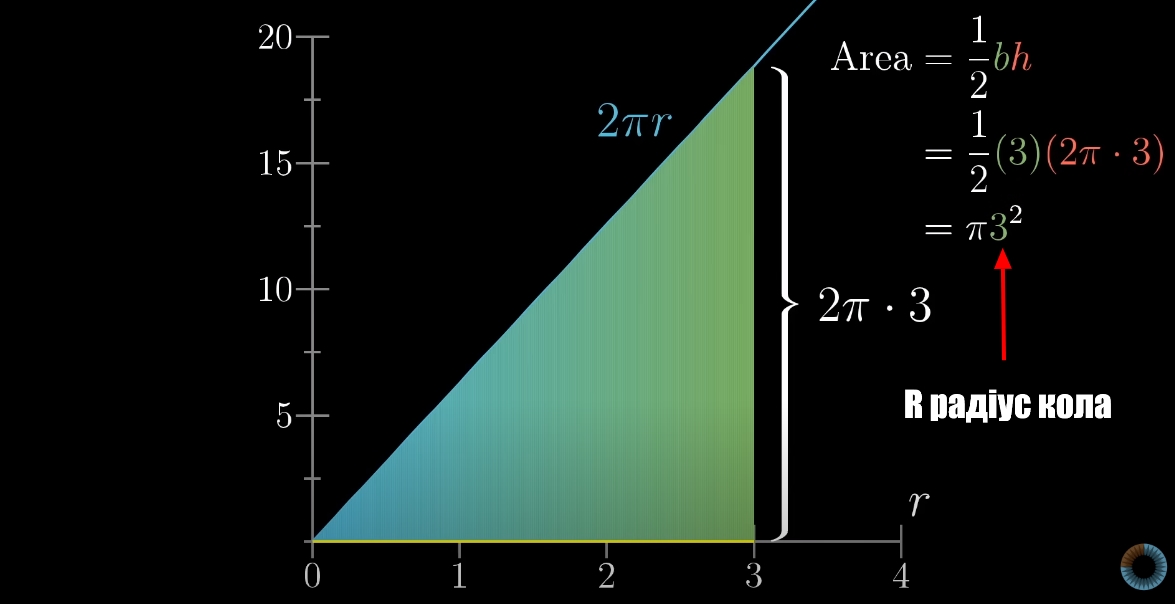
Площа трикутника Підставляючи R замість 3, отримаємо формулу площі кола.
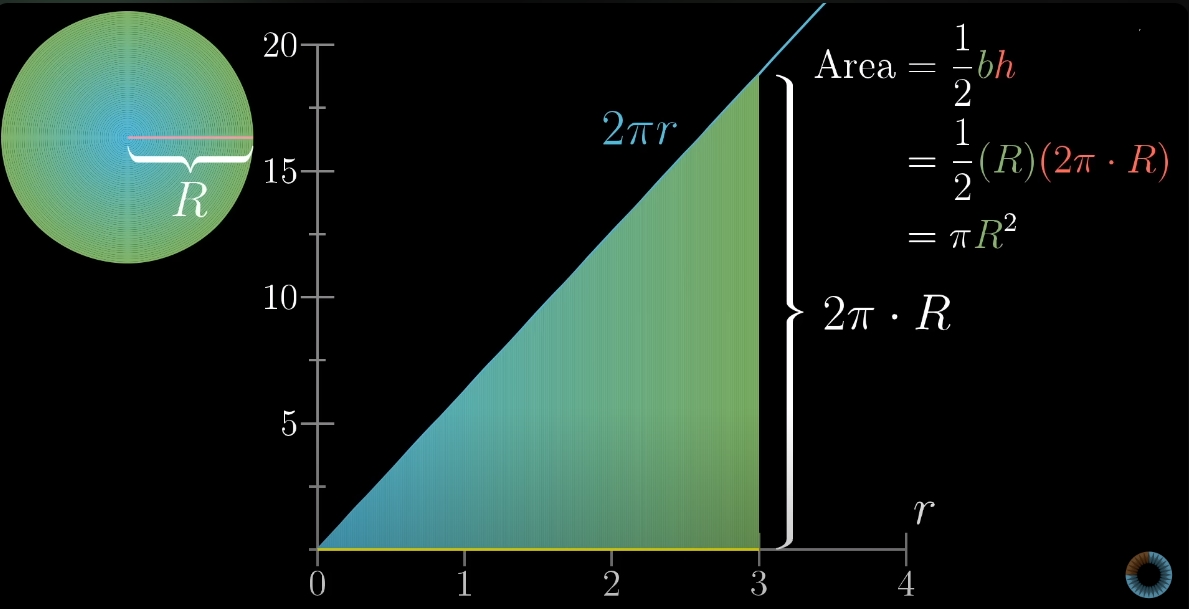
Виведена формула кола І знову ж питання, наскільки отримане значення точне? Продовжуючи зменшувати товщину розрізів до мільйонних, мільярдних і так далі, між розрізами майже не буде простору, але наскільки б тонкими розрізи не були, отримана таким способом площа кола все одно буде наближеним значенням.
Фух! Це біла цікава гра у розрізання кола, з подальшим перетворенням у суму прямокутників, з яких далі складається прямокутний трикутник. Ви винайшли формулу, застосовуючи найпростішу математичну операцію - суму. Як? Крутили та вертіли задачу, як кубика Рубика, поки не знайшли правильний кут, під яким видно рішення.
Зв’язок інтеграла та похідної
Зв’язок похідної та інтеграла називають “Фундаментальною теоремою обчислень”. Інтеграл в англомовних джерелах найчастіше називають “антипохідною”, і як на мене, цей термін краще пояснює природу інтегралу - протилежність до похідною.
Спершу, згадаймо, що таке похідна. Похідна - це зміна нахилу функції до осі Х на невеликому проміжку, простішими словами, наскільки функція чутлива до зміни Х. Надважливим аспектом у розумінні похідних є те, що вона показує зміну функцію на невеликому інтервалі, а не зміну в конкретній точці, в одну мить.
Найкраще це ілюструє наступний приклад: уявіть, що ви сідаєте в авто та їдете 500 метрів. Спочатку авто набирає швидкість, перед зупинкою швидкість знижується до повної зупинки. Функція дистанції буде виглядати ось так:
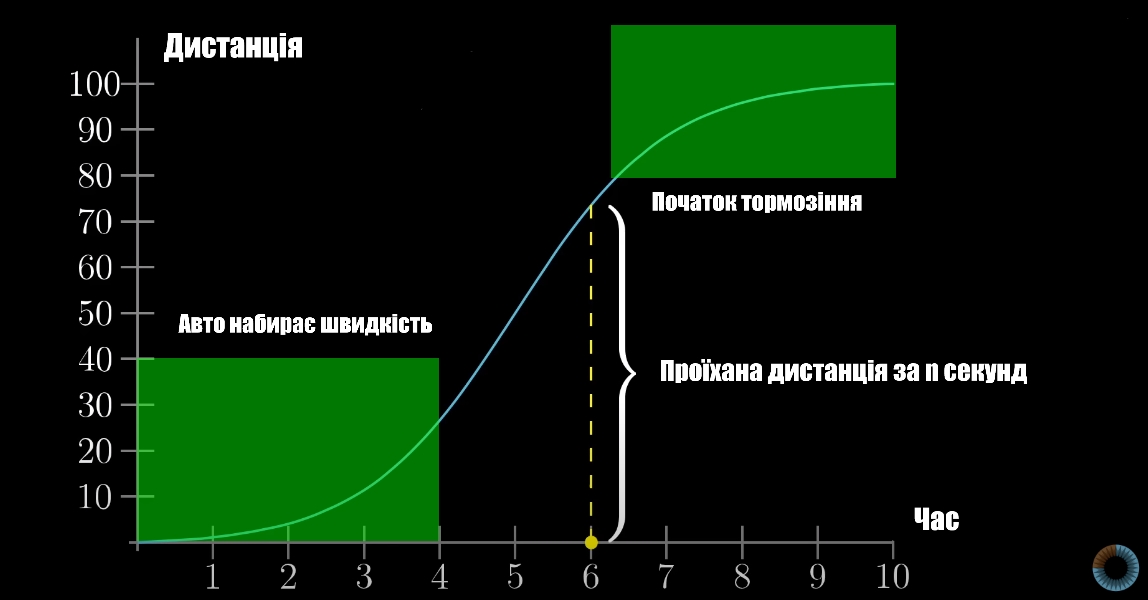
Але як знайти швидкість? Швидкість - це зміна проїханої дистанції за дуже короткий проміжок часу, іншими словами - це різниця між, наприклад, 0.1с та 0.2с, бо швидкості в конкретний час не існує (уявіть фотографію автівки, ви не зможете сказати її швидкість).
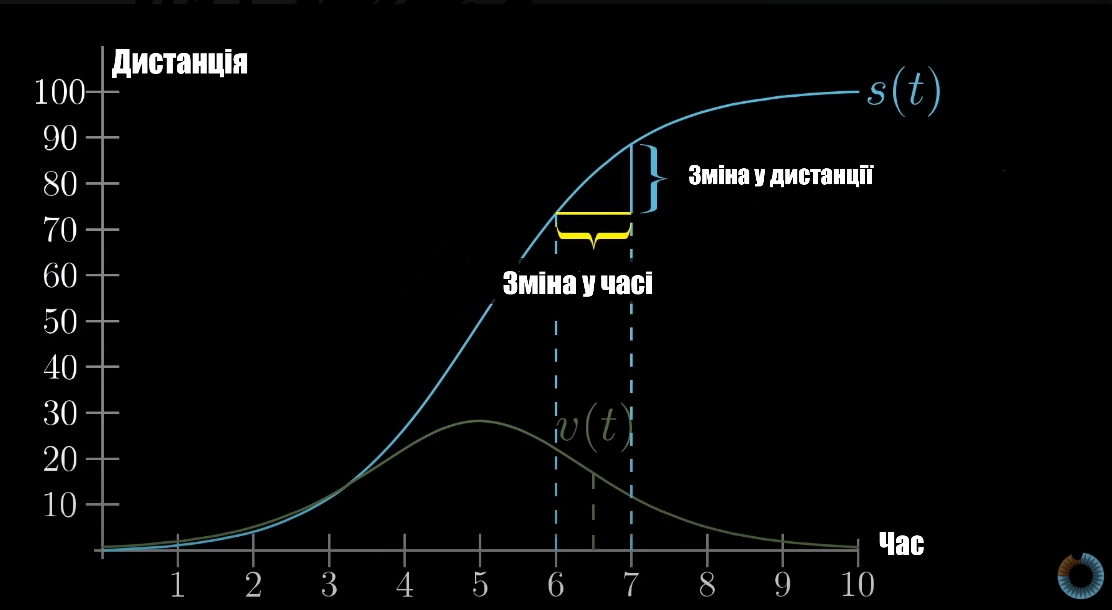
З цього виходить, що швидкість - це похідна дистанції. І справді, за перші дві секунди, різниця проїханої дистанції у проміжку між 1 та 2 секундах невелика, бо авто тільки починає набирати швидкість, у проміжку між 4—7 секундах зміна проїханої дистанції більша, авто їде з більшою швидкістю, між 9 — 10 секундах різниця ледь відчутна, бо авто майже зупинилося.
S(t) - функція дистанції, v(t) - функція швидкості, похідна дистанції.
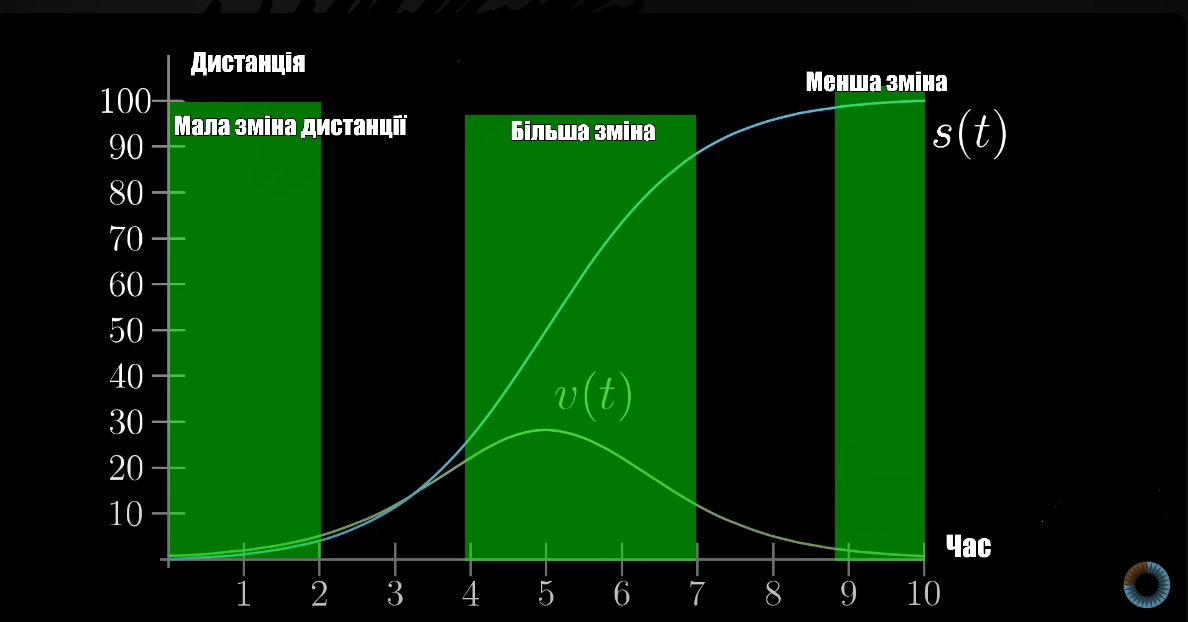
Проведіть уявну лінію нахилу, функції S(t) до осі Х, чим більший нахил, тим “яскравішою” буде похідна.
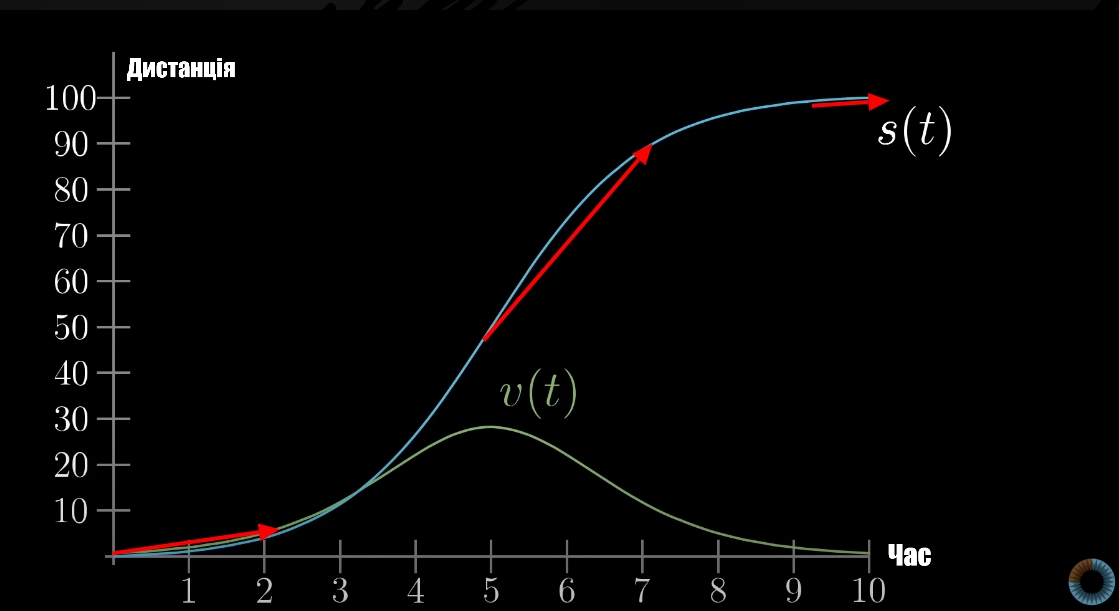
У проміжку між 4—7 секундами, коли авто починає прискорюватися, похідна v(t) помітно змінюється. Для кращого розуміння треба брати дуже малий інтервал (4.1с — 4.2с), але для ілюстрації взяла більший.
Наприклад, функція та похідна при швидкому старті та різкій зупинці буде виглядати так:
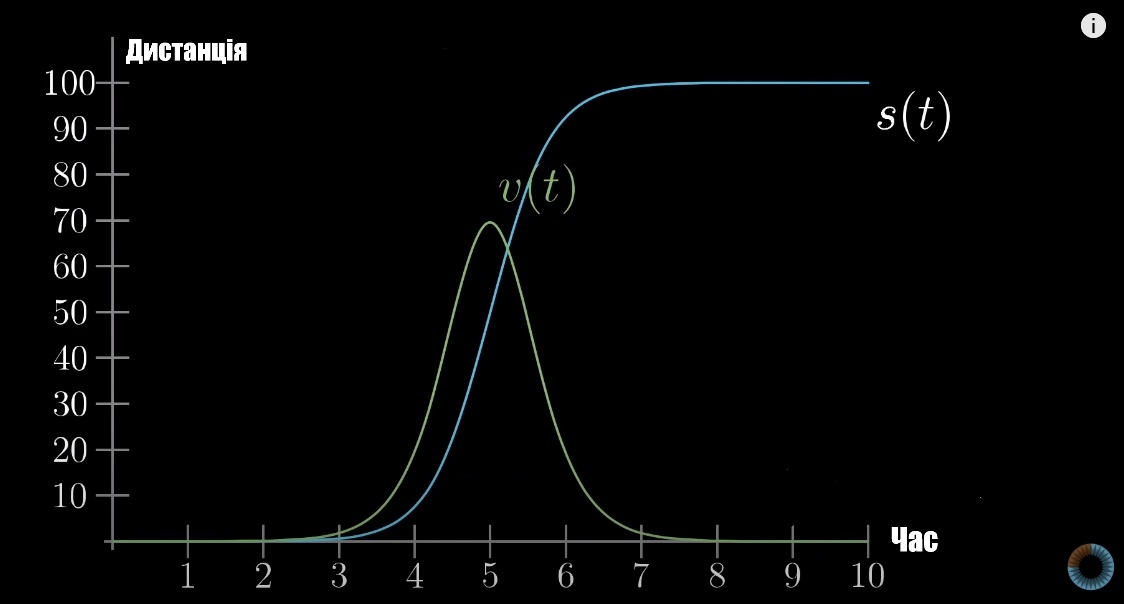
Але як знайти тоді швидкість? Швидкість = Дистанція/Час. Оскільки швидкість - це зміна функції дистанції у дуже маленькому інтервалі (для ілюстрації беру великий інтервал у 0.3с):
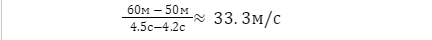
Дуже маленький інтервал - це інтервал, значення якого наближається до 0, наприклад, 0,00000000000000001 та 0,00000000000000002.
Тому, загальну формулу похідної можна записати ось так, де ds - зміна дистанції на дуже маленькому інтервалі, dt - зміна часу у дуже маленькому інтервалі.

Тут, зміна у дистанції виражена через дуже маленький часовий інтервал dt:
S(1c+0,00000000001) = S(1,00000000001)= 3м.
Похідна - це зміна функції за дуже короткий інтервал, у околицях однієї точки, але цей інтервал ніколи не буде дорівнювати 0, тобто ніколи не буде у конкретній точці. Без визначення інтервалу як такого, що наближається до 0, розрахунок похідної був би дуже складним. Це допомагає значно спросити похідну.

Фундаментальна теорема обчислень - зв’язок похідної та інтегралу
В український школах найчастіше пояснюють так: інтеграл - це “батьки” функції, похідна - “діти” функції. Таке пояснення є дуже простим, але не пояснює природу інтегралу. Інтеграл, або “антипохідна”, та похідна це взаємообернені операції. Спробуємо вивести формулу інтегралу самостійно, як з формулою площі кола.
Щоб пояснити інтеграл використаю як приклад ситуацію, обернену до написаної вище. Уявімо, що потрібно знайти дистанції, яку проїхало авто, використовуючи лише спідометр. Ви побудували ось такий графік, дивлячись на показання спідоментра. Математично, цей графік є похідною від функції дистанції, але у вас є лише спідометр, щоб знайти дистанцію. Щоб знайти функцію дистанції, треба зробити операцію, обернену до похідної, тобто, знайти інтеграл.
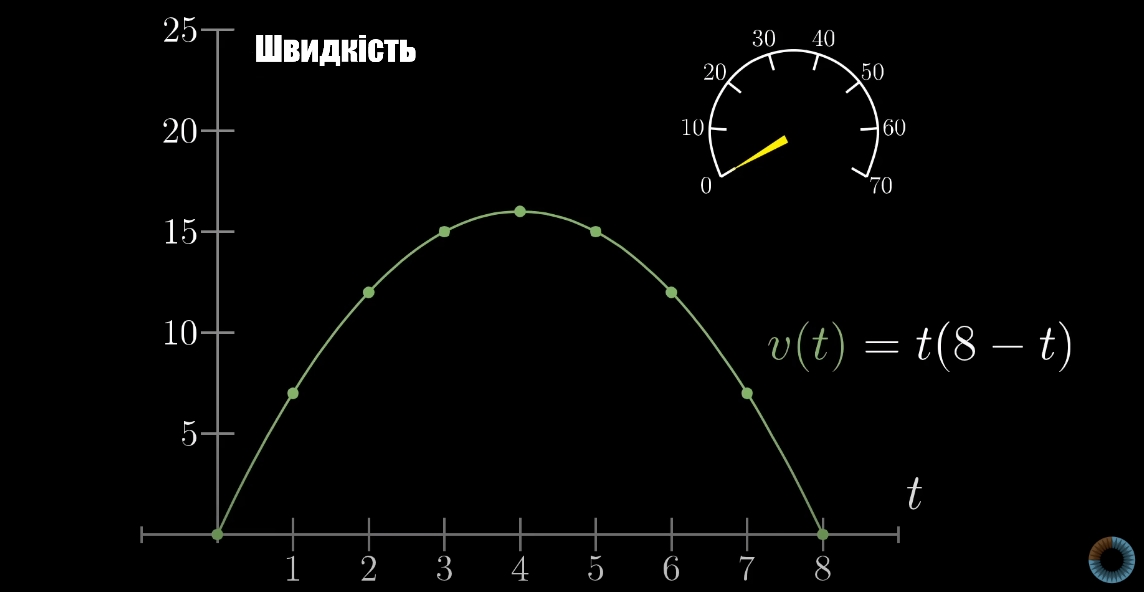
Функція швидкості v(t) не є лінійною, тому записана у вигляді полінома другого ступеня. Повернемося до визначення швидкості:
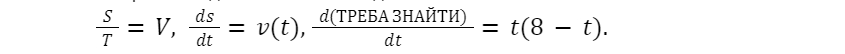
Але як знайти цю функцію S? Як і в найпершій задачі з колом, спробуємо знайти правильний кут, під який потрібно дивитися на задачу. Уявімо, що авто рухається за сталою швидкістю, тоді функція швидкості буде виглядати ось так:
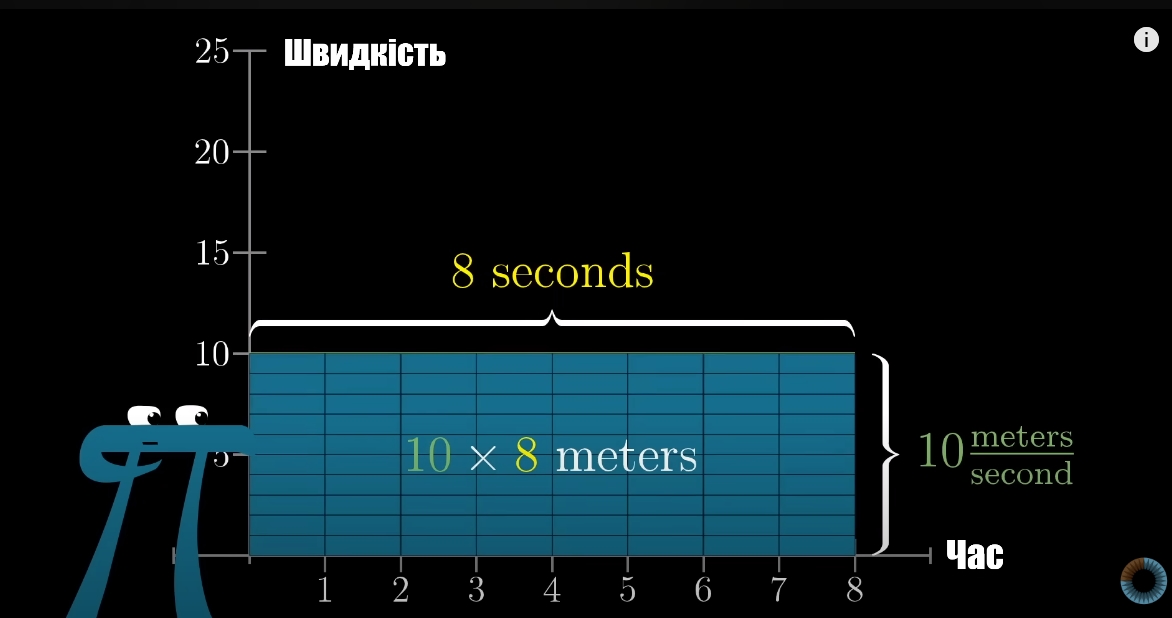
Виходячи з рівняння швидкості, дистанція S = VT, тобто, дистанція - це площа під графіком функції швидкості, у варіанті зі сталою швидкістю - площа прямокутника. Отримане таким способом значення проїханої дистанції буде наближене до реально значення. Ви можете сказати, це ж бред, як дистанція може бути площею прямокутника, і це дуже правильне питання. Як і в першому прикладі, якщо задача складна - потрібно спробувати розділити її на маленькі частинки, і потім знайти їх суму.
На які ж частини найлегше для обчислення розділити наш графік швидкості? Знову, прямокутники. У якій ситуація такий спосіб може спрацювати? Якщо авто їде з однаковою швидкістю протягом кожної півсекунди. Швидкість у 1.5 сек. більша, ніж у 1 сек., але оці півсекунди між 1.5сек та 1 сек. авто їде зі сталою швидкістю.
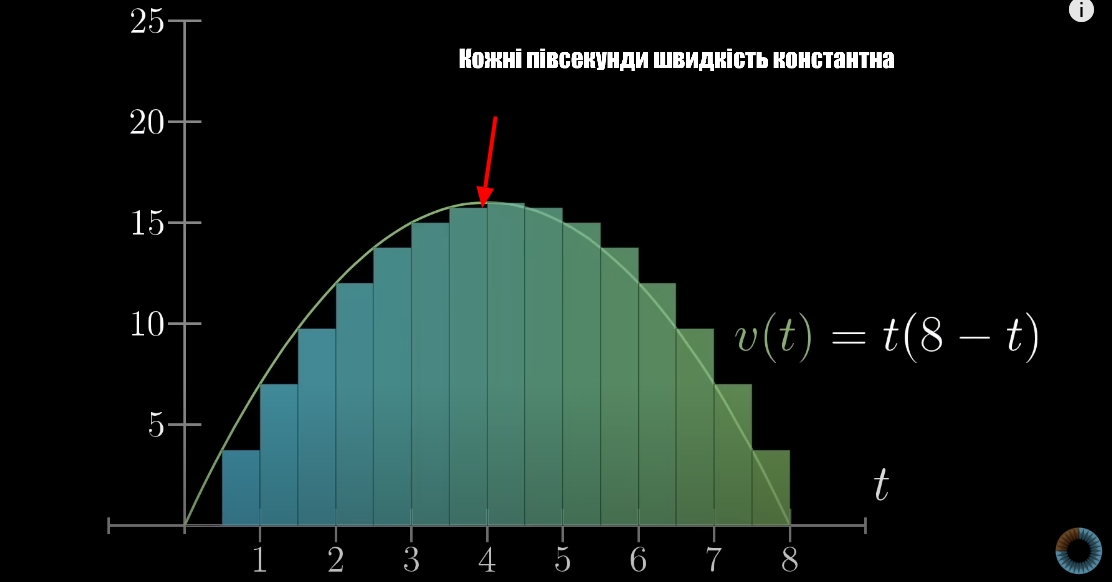
Виходить доволі негарно, але якщо зменшити інтервал сталої швидкості, прямокутники будуть краще вписуватися під форму графа.
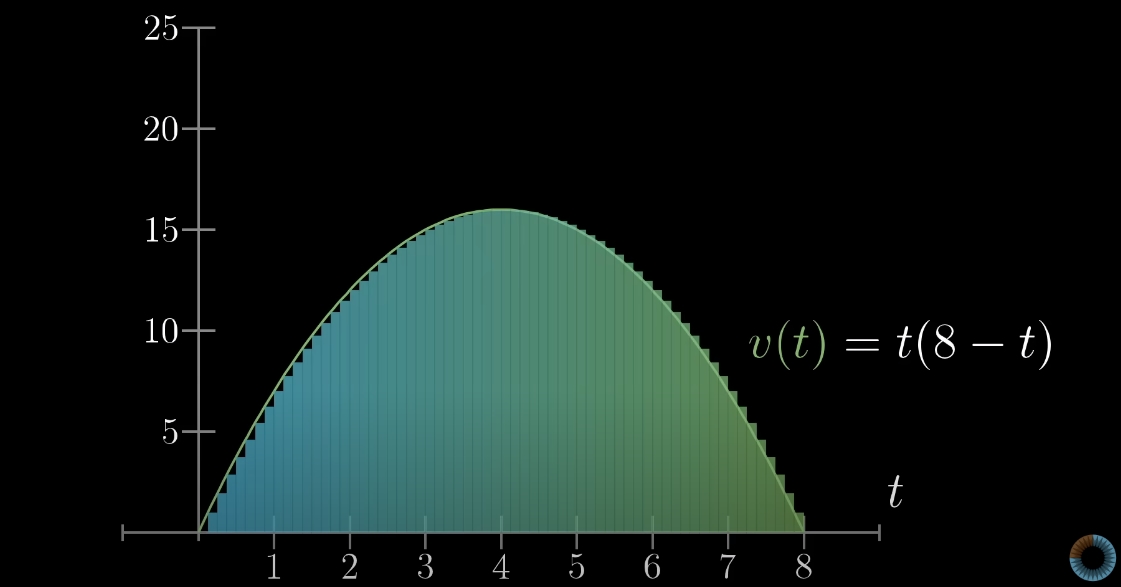
Тепер спробуємо знайти площу якогось прямокутника.
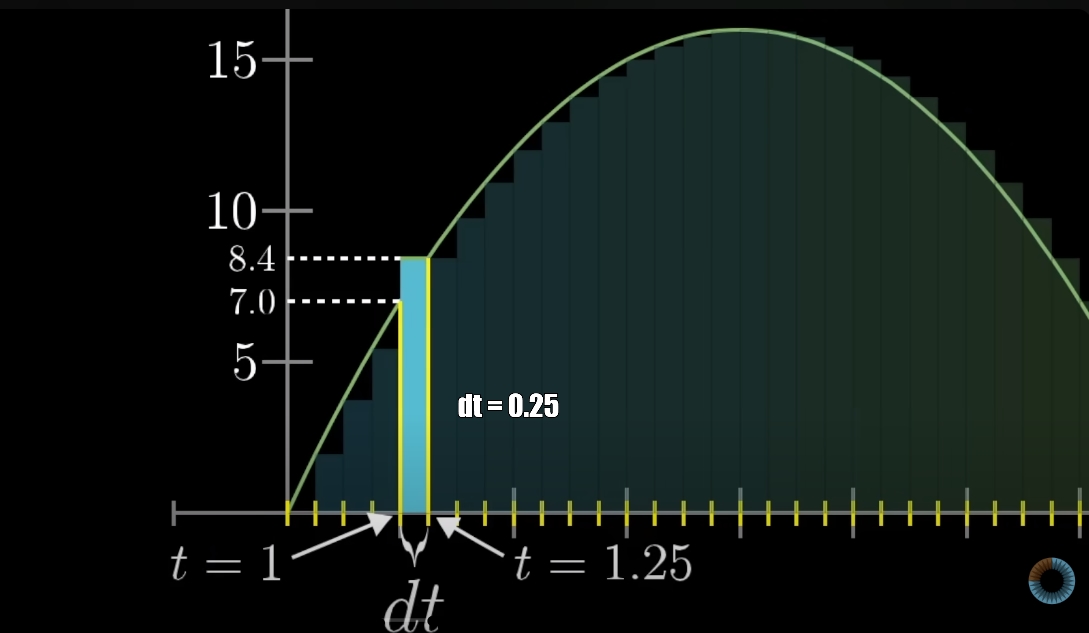
Нехай швидкість буде стала на інтервалі у 0.25 сек, тоді ширина прямокутника буде 0.25, але як визначити довжину? Чи взяти більше значення швидкості, 8.4, чи менше, 7? Це не має значення, чим менше інтервал, тим краще прямокутники будуть вписуватися під граф функції.
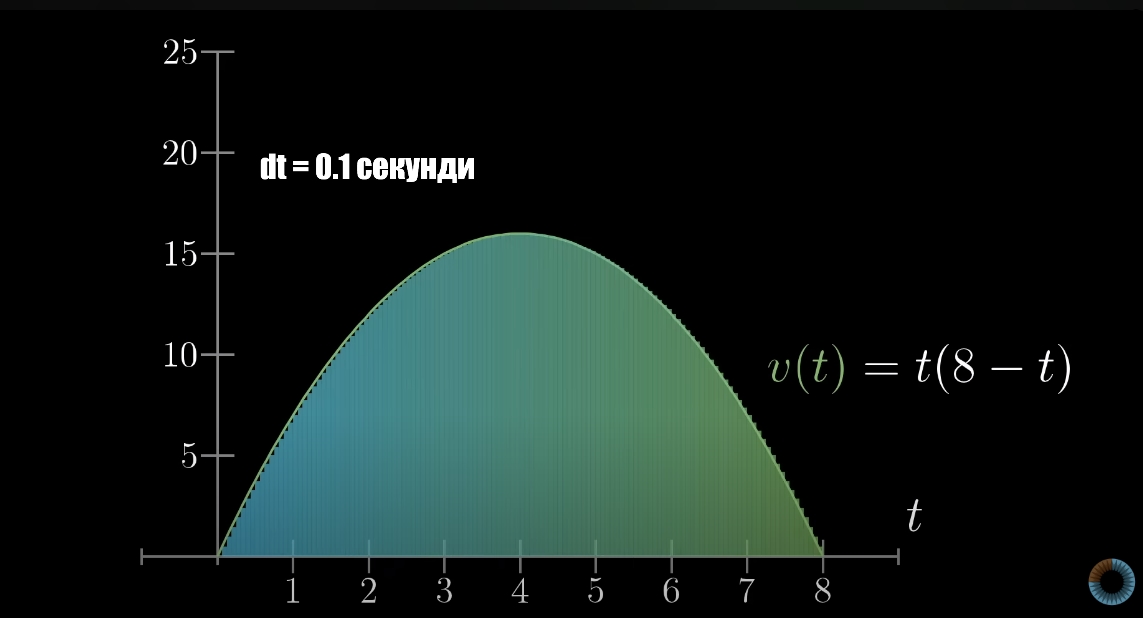
Чим меншим буде інтервал, тим більш “плавніше”, без помітних скачків, буде рухатися змодельоване авто.
Загальна формула площі кожного прямокутника буде: v(t)dt
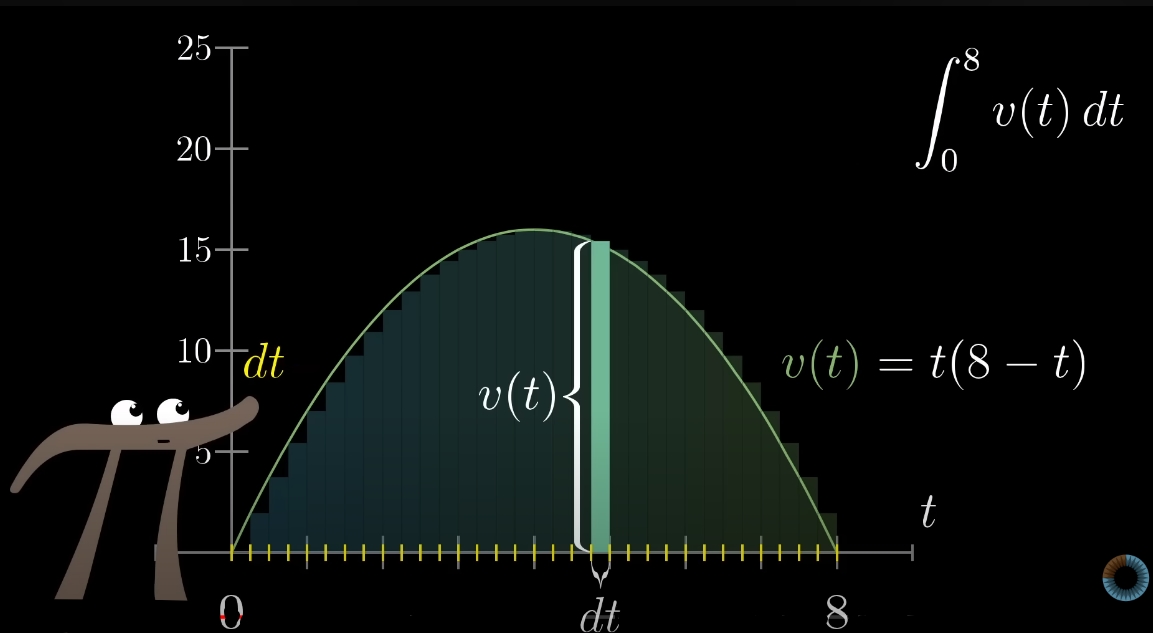
Прекрасно! Тоді, для знаходження площі під функцією, треба просумувати площі всіх прямокутників? Як казала раніше, інтеграл - це операція, обернена до похідної, а сума явно такою не є. Інтеграл повинен стояти “вище” функції, тобто мати якісь ознаки більшості - а саме, показник степені. Навіщо ж це робити? Чим вища степінь полінома, тим складнішу він має форму. Площі під таким складним поліномом неможливо знайти, використовуючи просто суму, наскільки б маленьким не був інтервал, наскільки б добре мільйони маленьких прямокутників не вписувалися під графік функції. Значенням інтегралу буде площа під кривою, графіком, саме інтегралу.
Важливо запам’ятати, що хоч сума та інтеграл мають схоже написання, вони є різними операціями:
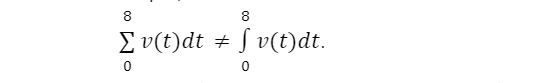
dt у сумі буде мати константне значення, тобто, навіть з самим маленьким інтервалом, “шпаринки” між прямокутниками залишаться, тоді як dt у інтегралі завжди буде наближатися до нуля (через це інтеграл іноді розглядають як ліміт суми) — “шпаринки” будуть непомітними.
Для цього прикладу площа фігури під інтегралом, не функції, буде дистанцією, яку проїхав автомобіль.
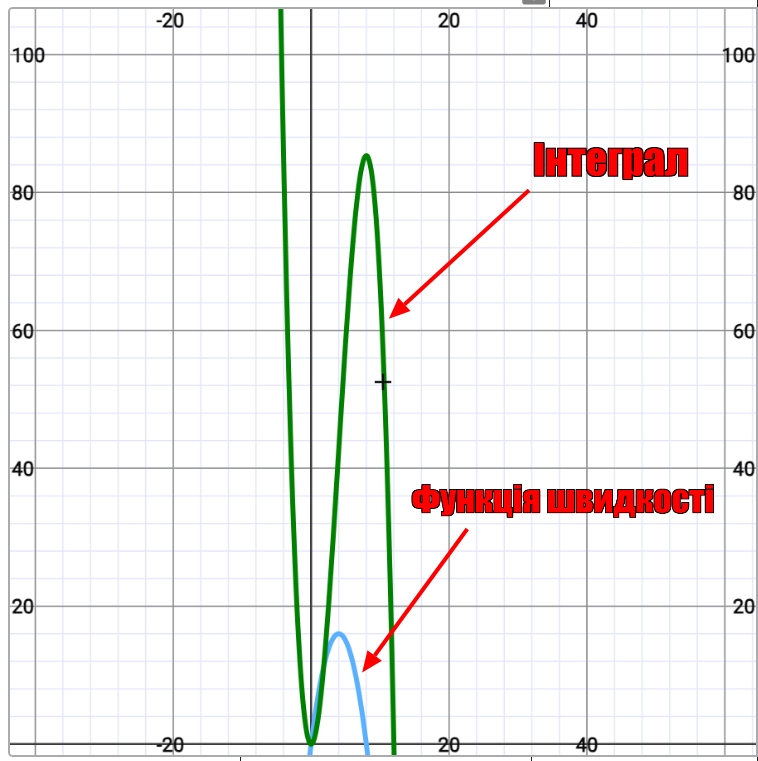
Ще одним важливим аспектом інтегралу є вільна константа С, що відповідає за “рух” функції по осі Y.
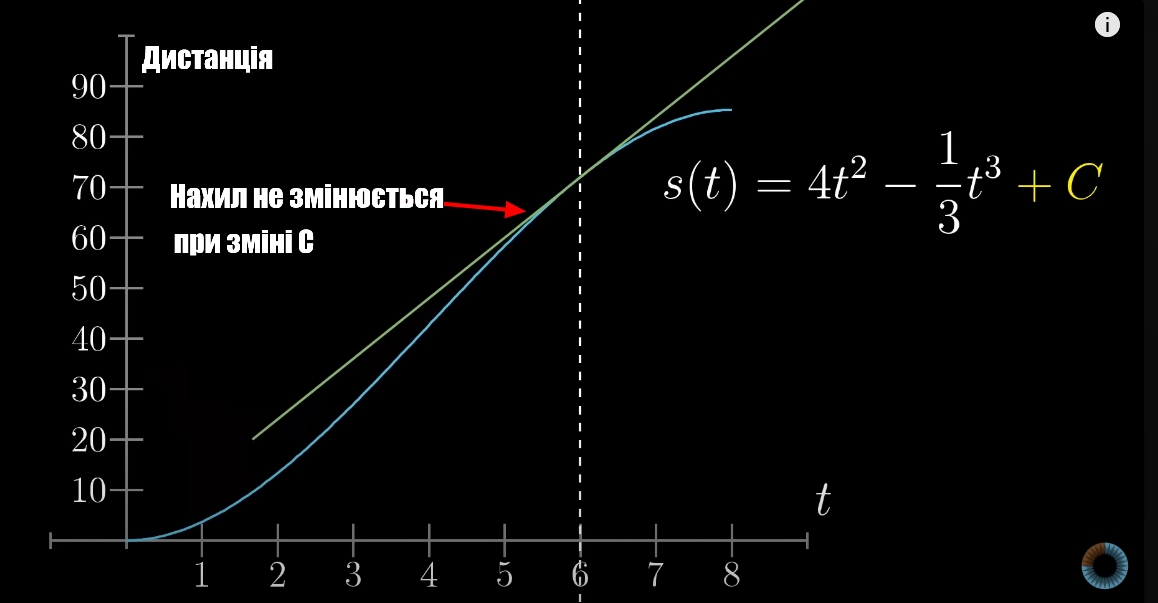
Скільки б ви не піднімали чи опускали функцію дистанції, як на картинці вище, нахил функції до осі Х, тобто похідна, не зміниться - функція залишиться з власними властивостями. Тобто, інтегралів до функції є безліч, через що функція не прив’язана до одного конкретного інтегралу з одним значенням С. Покажу на прикладі.
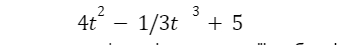
- є функцією дистанції, тобто, інтегралом до нашої першої функції швидкості. Щоб знайти функцію швидкості, потрібно взяти похідну від інтегралу. Правила інтегрування кажуть, що константи стають 0, тобто отримуємо ту саму функцію швидкості: t(8-t).
Але, це працює тільки з невизначеними інтегралами (ті, які не мають меж), як у попередньому прикладі. Мені допомагає такі порівняння: невизначений інтеграл - це корабель без якоря, хвилі можуть його піднімати та опускати, тоді як визначений інтеграл має якір, він стоїть на місці, “прив’язаний” до своєї осі. Саме визначений інтеграл є значенням площі під кривою, конкретним числом, а самі межі інтегралу підставляються у невизначений інтеграл. Приклад:
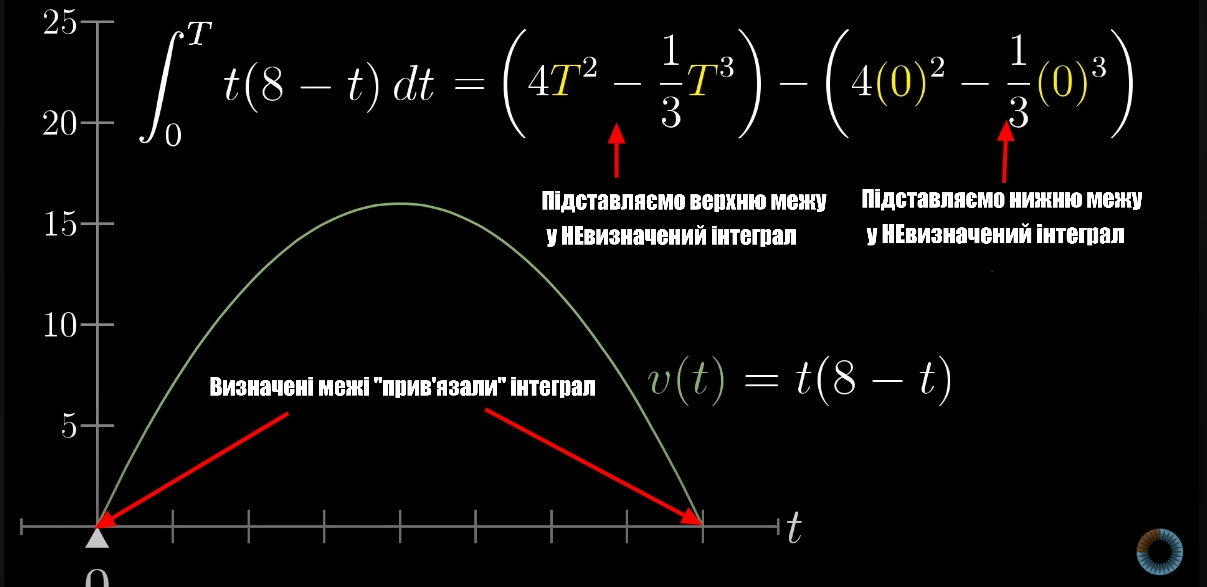
Нижня та верхня межа можуть бути будь - якими числами.
Навіть якщо додати константу С до визначеного інтегралу, вона анулюється віднімання верхньої межі від нижньої.
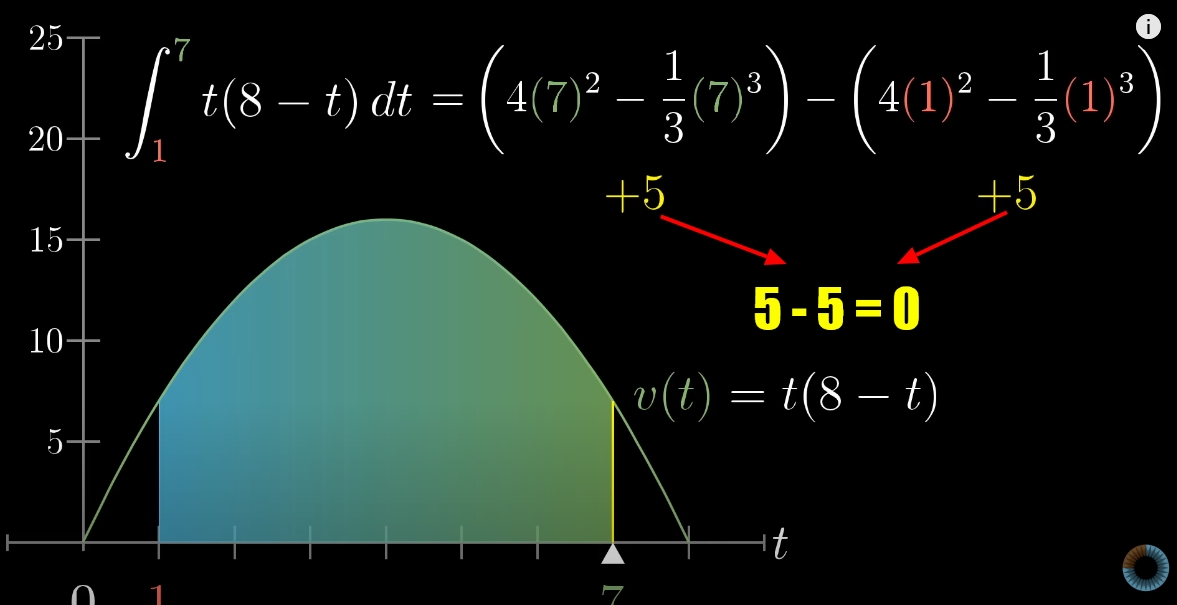
Фух, цей розділ дуже добре погрався зі свідомістю, давайте пригадаємо всі основні моменти. Я намагалася якомога простіше пояснити саму суть інтегралу, але за цією суттю йдуть дуже цікаві частні випадки, які трапляються вже в наукових сферах.
Recap
Інтеграл та похідна - взаємообернені операції.
dt,dx, d з будь- якою літерою - це показник дуже маленького інтервалу, дуже маленьких змін.
dt0 завжди наближається до нуля, задля вписування прямокутників ідеально під графік.
Інтегрування та сума - це різні операції.
Невизначений інтеграл - це формула, визначений інтеграл - це площа під графіком невизначеного інтегралу.
Визначений інтеграл “прив’язаний” до осі, тоді як до невизначеного потрібно додавати константу.
Визначений інтеграл знаходиться шляхом знаходження різниця між невизначеним інтегралом куди підставлена верхня межа, від невизначеного інтегралу, куди підставлена нижня межа.
У наступних розділах розглянемо конкретні приклади знаходження як визначеного, так і невизначеного інтегралу.
Техніки інтегрування
Передмова: я, як і доволі багато студентів інженерних спеціальностей, мала труднощі з чітким упорядкуванням, якою технікою який вид інтегрування треба вирішувати. У університетських посібниках я не знайшла чіткої класифікації, знайшла її у підручнику MIT Calculus 2. Тепер трохи про Calculus 2. В американській системі інший розподіл тем. Precalculus - це основні операції, дроби, прості рівняння, тощо - на рівні 7 класу наших шкіл. Calculus 1 - це ліміти, похідні першого ступеня, ряди. Calculus 2 - інтеграли, похідні різних ступенів, об’єми складних тіл, тощо. Calculus 2 зазвичай починають вивчати вже в університеті або коледжі.
Загальний порядок дій:
Спробувати вирішити інтеграл через додавання, множення (power rule).
Якщо не вдається, вирішувати за допомогою u-substitutional.
Якщо обидва варіанти не підійшли, переходити до інших методів.
Техніка заміни (U-substitutional)
Це проста техніка заміни, яка полягає у тому, щоб всі частини інтегралу визначити через u та du наступним чином: u - повинно підставлятися у ту частину рівнняння, похідна якої є іншою частиною інтегралу, оскільки du - це похідна u. У цій техніці замінюється і dx.
Приклад 1: Інтегрування u-sub
Розв’яжемо цей інтеграл:
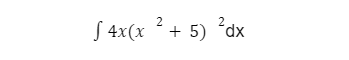
Через похідну якої частини рівняння можна виразити весь інтеграл?
Якщо взяти 4x, похідна 4х це 4, через що не можна виразити (x^2+5)^2. Якщо ж взяти (x^2+5), похідна буде 2х, через неї можна виразити іншу частину інтегралу - 4х.
Інтеграл має 3 частини, які потрібно замінити: 4x, (x^2+ 5)^2, dx.
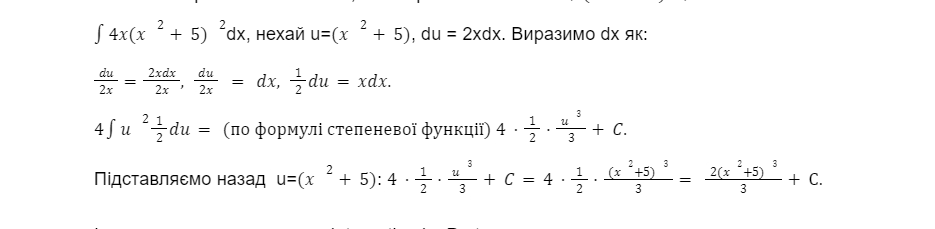
Інтегрування по частинам - Integration by Parts
Ця техніка проста, але дуже ефективна. Щоб розуміти техніки інтегрування, потрібно знати на яких математичних законах вони базуються. Це може бути нудно, але обіцяю, це допоможе краще розуміти їх та не гуглити кожен раз.
Інтегрування по частинам базується на законі добутку (product rule) - це диференціальний добуток двох та більше функцій. Диференціальний добуток не є “звичайним” добутком, світ був би набагато простішим, і в плані технологій, якщо для чисел та функцій добуток працював однаково. Дуже грубо та поверхнево кажучи, диференціальний добуток працює не в одній площині, як добуток чисел, а в багатьох. Тобто, оскільки кожна функція розташована у власній площині, диференціальний добуток повинен “перемножувати” площини обох функцій.
Наприклад, функція y = x^2cos 3x є добутком двох функцій: x2 та cos3x. Ми можемо взяти інтеграл або похідну від кожної функції окремо, але щоб взяти похідну або інтеграл від функції y, потрібно використовувати правило добутку.
Правило добутку
Перепишемо функцію як h(x) = f(x)g(x), де f(x)=x^2, g(x)= cos 3x. Правило добутку каже. що похідна h(x) - це сума добутків похідної першої функції та другої, похідної другої функції та першої функції:
h′(x) = f ′(x)g(x) + g′(x)f(x)
Тепер спробуємо інтегрувати, щоб отримати функцію h(x):

- сума функцій під одним інтегралом може бути розділена на 2 та більше інтегралів, dx потрібно приписувати до кожного інтегралу (dx - неймовірно малі зміні на інтервалі).
Тепер маємо суму двох інтегралів, кожен з яких є добутком функції та похідної.
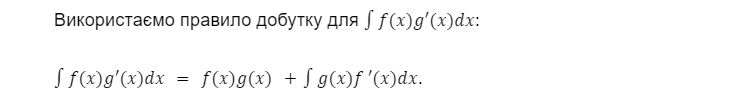
І справді, інтеграл повинен бути “оригінальним” добутком f(x)g(x). Для легшого запам’ятання формули замінимо на u та v:
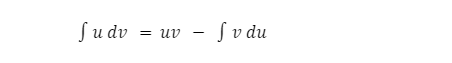
— u та v - функції, dv та du - їх похідні.
Інтегрування по частинам розбиває складний інтеграл на простіший. Виходячи з правила добутку, інтегрування по частинам використовується, коли інтеграл містить добуток двох функцій. Але, якщо інтеграл містить добуток під коренем, інтегрування по частинам не спрацює. Добуток повинен бути “чистим”.
Приклад 1: Інтегрування по частинам
Не можна казати, що u = x, dv = sinx тільки по червоговості написання. Черговість для добутку не важлива. Тому, треба спробувати всі варіанти:
Варіант 1: u = sinx, dv = x, тоді du = cosx (похідна sinx), v= x22 ( v - це функція, dv - похідна цієї функції, тобто, щоб знайти функцію, потрібно взяти інтеграл від похідної). Цей варіант навпаки ускладнить інтеграл.
Варіант 2: u = x, dv = sinx, du = 1dx, v = - cosx. Така підстановка спрощує інтеграл, її і буду використовувати.
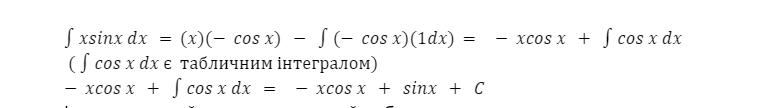
І ось, страшний тригонометричний добуток перетворився у просту суму.
Напевно ви чули, що хороший математик - лінивий математик. При використанні будь - якої техніки інтегрування, задача - це максимально швидко та правильно знайти рішення. Можливо у вас виникло питання, чи є якась підказка по вибору u та dv. Так, вона є, і, що іронічно, її акронім співзвучний до Ліліт.
LEATE — метод знаходження u та dv
Акронім LIATE ( Logarithmic Functions, Inverse Trigonometric Functions, Algebraic Functions, Trigonometric Functions, Exponential Functions), української так само, використовується ось так: яка функція інтеграла є першою у с акронімі, та функція і є u.

Тригонометрична функція хоч і є першої в інтегралі, але в акронімі йде після логарифмічної, тому u = логарифмічна функція, dv = тригонометрична функція.
Приклад 2: Застосування LEATE
Використаємо акронім, простіше буде переписати інтеграл ось так:

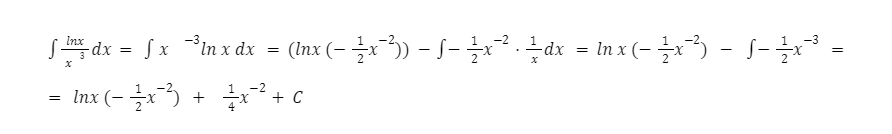
Навіть такий неприємний дробний інтеграл можна вирішити у кілька строк. Якщо вам не подобаються дроби, їх можна переписати у вигляді добутку, але з негативними степенями.
Приклад 3: Коли LIATE не працює
Такі інтеграли доволі рідкісні, але і LIATE є тільки підказкою.

Приклад 4: Застосування інтегрування по частинам більше, ніж 1 раз
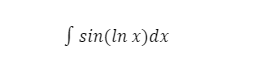
цей інтеграл не є добутком, на відміну від попередніх прикладів, тобто, в інтегралі є тільки є функція - sinx. Але як же тоді обрати u та dv? У таких випадках за u або dv використовують 1 (найчастіше за все за dv):

Подвійне інтегрування по частинам видається дивним, але зробивши декілька аналогічних вправ дивність зникає.
Інтегрування по частинам: Визначений інтеграл
На цей вид інтегралів переноситься все те ж саме, що працювало для невизначених інтегралів. Окрім, як казала раніше, константи C - вона вже не потрібна, оскільки інтеграл “прив’язаний” до осей через верхню та нижню межу визначеного інтегралу.
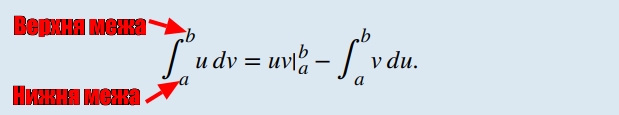
Ці межі “окреслюють” інтеграл. Завдання “Знайти площу під кривою” фактично означає вирішити визначений інтеграл.
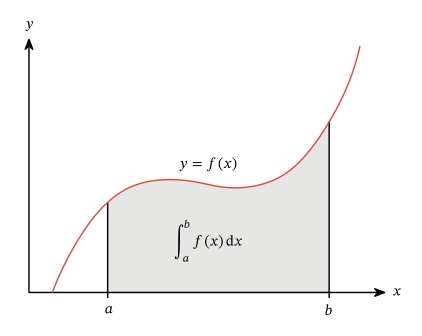
Приклад 1: Знайти площу між y = tan^(-1)x та віссю X на проміжку [0,1]
Проміжок дійсних чисел завжди пишеться у квадратних дужках, позитивна/негативна безкінечності - у круглих.
Щоб знайти площу, потрібно вирішити визначений інтеграл
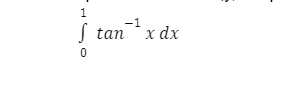
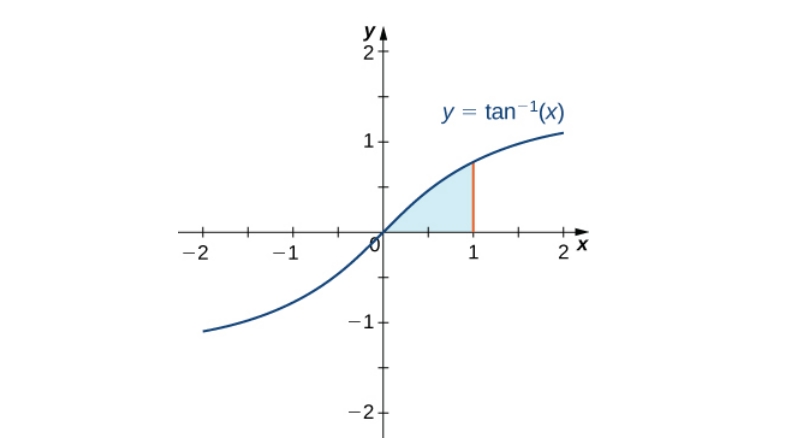
Не мали б інтеграла, будували б мільйон тоненьких прямокутників, а потім знаходили площу як їх суму. На щастя, інтеграл дозволяє знайти площу у кілька строк. Хоч інтеграл і не є добутком функцій, оскільки має тільки одну, але це все ще не табличний інтеграл.

Як бачите, навіть найнеприємніший на вигляд інтеграл можна швидко вирішити.
Тригонометричні інтеграли
Тригонометричні інтеграли вважаються одними із найскладніших у розв’язанні, але тільки якщо не знати правильну техніку. Вони складаються з добутку тригонометричних функцій. Сама техніка інтегрування є частиною Trigonometric Substitution - об’ємною теми, частину з якою розкажу у цій главі.
Тригонометричні інтеграли використовуються для розрахунку у різних системах, тому, якщо ви не працюєте у цій області, зустрічаються доволі рідко. Ця тема дуже велика, тому тут опишу тільки основні моменти, від яких, якщо потрібно, можна вивчати далі.
Тригонометричні інтеграли як добуток або степінь з sinх та cosх
Основні кроки полягають у:


Приклад 1: Коли k - непарна степінь
Інтеграл виду:
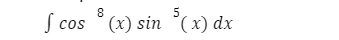
Для вирішення підходить тільки 1 випадок.

Тригонометричні інтеграли як добуток або степінь з tanx та secx
Перш за все, sec (секант) - це не котангенс. Хоч для нас більш звичним є котанганс, але основними тригонометричними функціями є сінус, тангенс та секант.
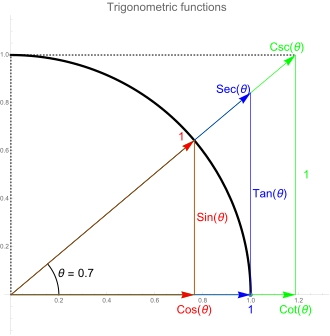
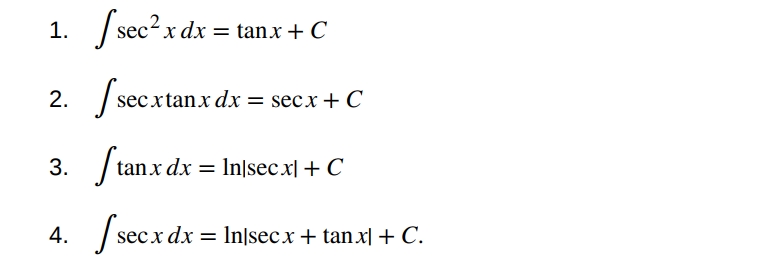
Аналогічно з синусом та косинусом, алгоритм дій такий:


Приклад 1: Коли j парної степені
Для цього прикладу підходить тільки 1 варіант, на відміну від степенів синуса та косинуса, тут останній пункт має степені різної парності.

Фух, це може здаватися спочатку незвичним, тому пропоную переглянути більше прикладів тут.
Тригонометрична підстановка (Trigonometric substitution)
Частиною цього розділу є тригонометричний інтеграл. Тригонометрична підстановка застосовується до інтегралів, які містять квадратний корінь у формах:
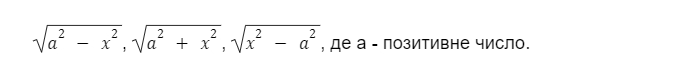
Основна ідея - це переписати інтеграл у вигляді тригонометричного інтегралу.
Доречним буде питання, чи настільки важливо робити саме таким способом? Так. Іншими техніками інтеграл з коренем розв’язати неможливо.
Тож, трохи теорії як працює ця підстановка.


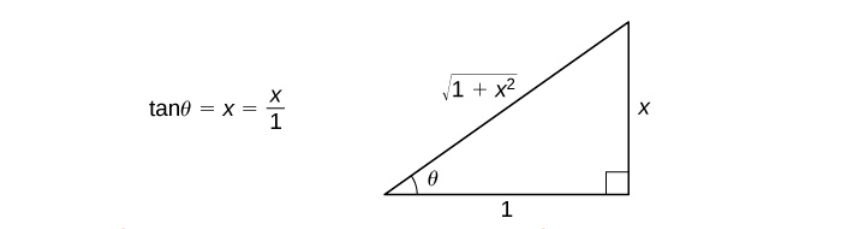
Приклад 1: Інтеграл 1 виду
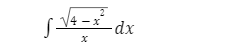
З першого погляду виглядає не дуже дружелюбно (з другого теж), але спробуємо подружитися. Зробимо заміну, як підказує другий пункт:
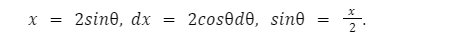
Щоб краще зрозуміти, раджу малювати ось такий трикутник:
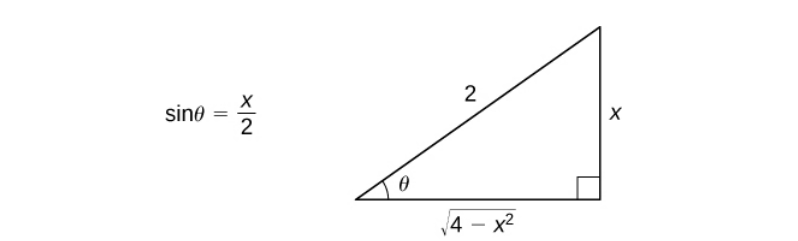

Такий вид інтегралів є найскладнішим з Calculus2, оскільки підстановку потрібно робити, дивлячись на трикутник.
Приклад 2: Інтеграли 2 типу


Розв’яжемо інтеграл та намалюємо референсний трикутник
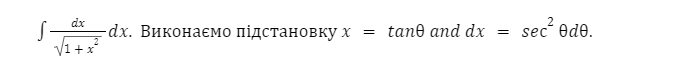

Приклад 3: інтеграли 3 типу
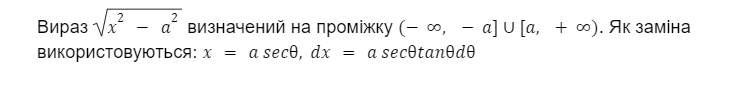

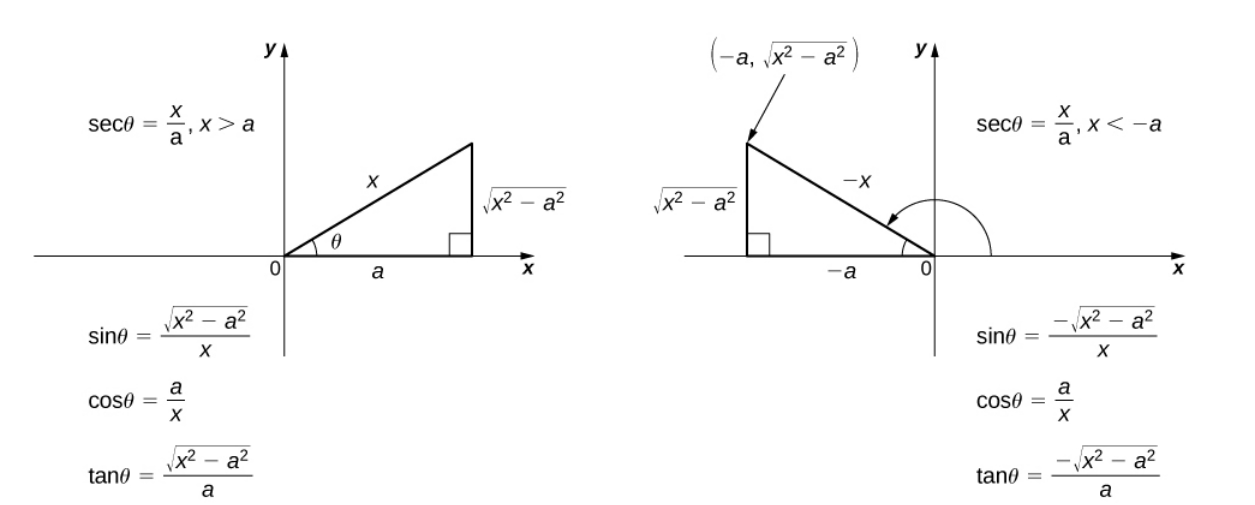
Завдання: знайти площу між f(x) = x^2 − 9 та віссю X, на проміжку [3,5]
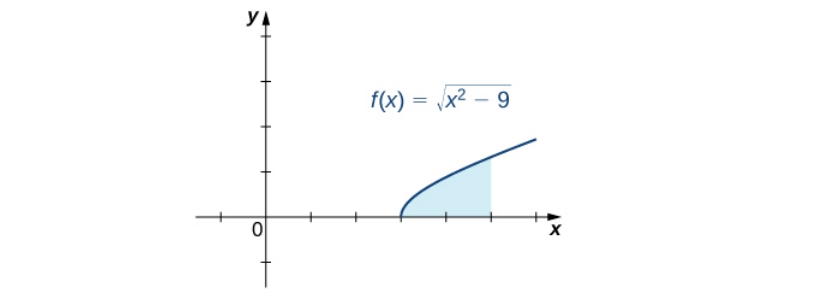
Також потрібно замінити межі визначеного інтегралу на:
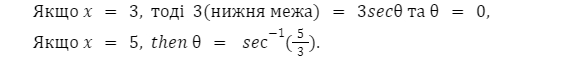

Частковий розклад (Partial Fraction)
Ця техніка працює з поліномними (багаточлен) інтеграли. Чому для поліномів потрібна окрема техніка? Ви вже знаєте як розв’язати інтеграл з раціональними функціями - за однією з технік вище або, розклавши, вивести табличний інтеграл. Проте. такі функції не мають довільних часток, які мають поліноми.
Суть техніки - це розкласти складний поліном на складові, які вже можна розв’язати.
Наприклад,

Розкладання в цьому випадку - це знаходження коренів полінома у знаменнику, за Вієта чи дискримінантом.
Поліноми записують у вигляді P(x)/Q(x), техніку часткового розкладу можна застосувати тільки тоді, коли степінь чисельника менша, ніж степінь знаменника, deg(P(x)<Q(x))).
Загальний алгоритм є наступним:

Перший випадок, коли степінь чисельника менша, ніж степінь знаменника, вже побачили. Перейдемо до випадку, коли степінь чисельника більша.
Приклад 1: deg(P(x)>Q(x)))
У цьому випадку потрібно зробити ділення полінома у чисельнику, на поліном у знаменника. Це називається Long Division (ділення поліномів).

Приклад 2: Поліном містить неповторювальні фактори (Випадок 3a)
Бувають випадки, коли степінь чисельника хоч і менша, за степінь знаменника, але поліном не можна розкласти:
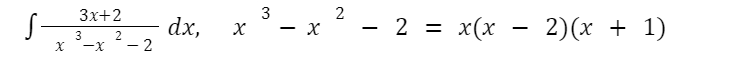
У таких випадках використовують розклад полінома за константами A,B,C:
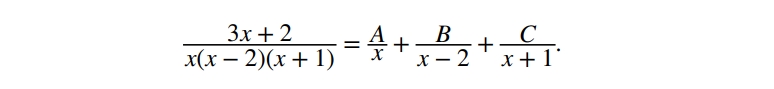
Зводячи до спільного знаменника, отримаємо:
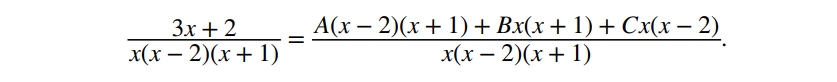
Прирівнюємо чисельник до чисельника, щоб знайти значення A,B,C:
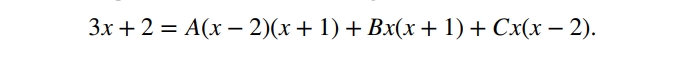
Існують два методи для знаходження A,B,C - Метод прирівнювання коефіцієнтів та Метод стратегічного заміщення. Як на мене, перший простіший.


Отримані значення коефіцієнтів підставляємо:
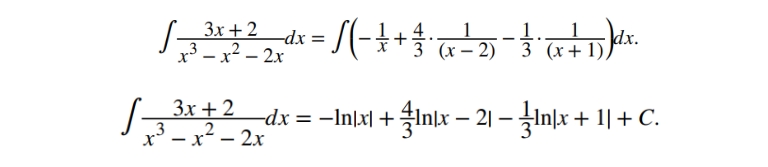
Приклад 3: Поліном містить повторювальні фактори (Випадок 3b)
Якщо поліном (найчастіше знаменник) містить степеневий фактор, його потрібно розписувати ось так:
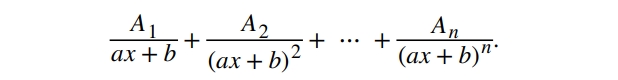
Розв’яжемо інтеграл:
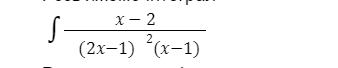
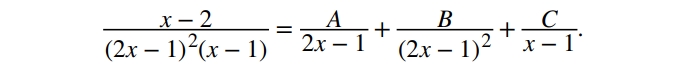
Зверніть увагу, що (2х-1) повторюється два рази: спочатку у першій степені, потім у другій. Прирівнюємо чисельники:
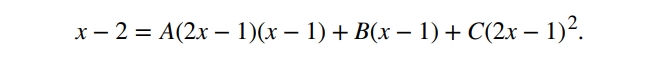
Розкриваємо дужки:
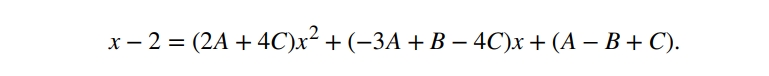
Використовуючи один з верхніх методів, отримаємо: A = 2, B = 3, and C = −1
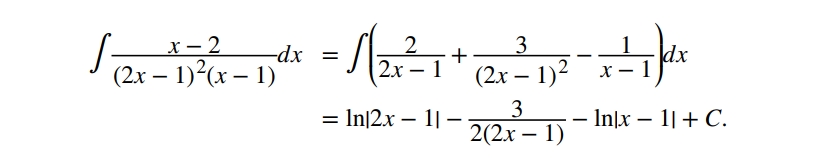
Я відбирала приклади, які трапляються найчастіше. Але дуже раджу подивитися більше на сторінці 313.
Інші техніки інтегрування та числові методи визначеного інтегралу
Інтеграли можна розв’язувати і за допомогою електронного калькулятора CAS, але раджу ним користуватися, тільки якщо є базові знання інтегралів і розуміння технік інтегрування.
Як казала раніше, визначений інтеграл - це наближене значення площі під кривою. Але, щоб це значення було максимально наближеним, потрібно обирати один з декількох методів, в залежності від виду інтеграла.
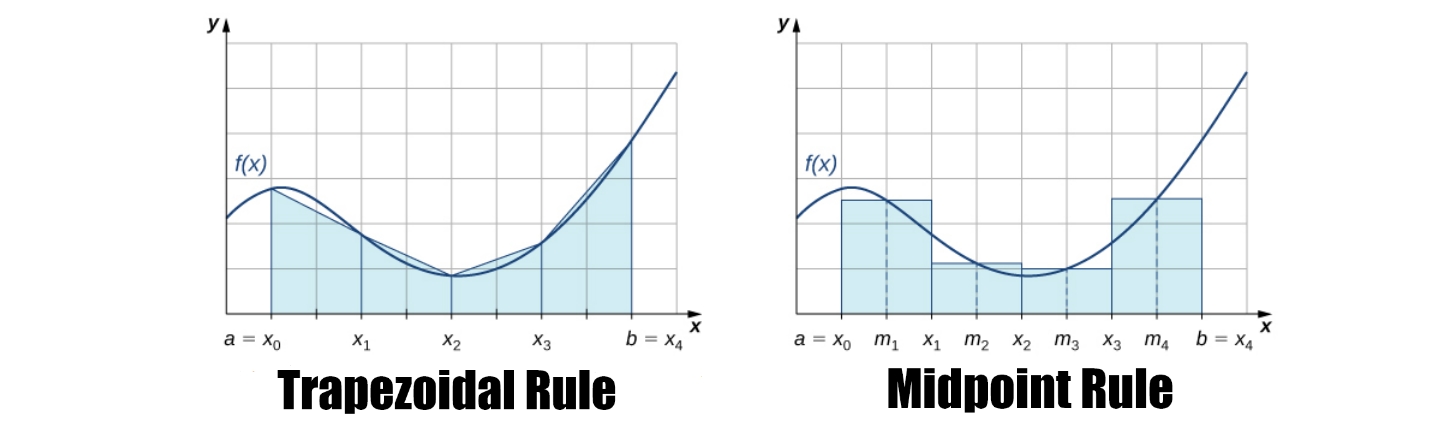
Один з найперших прикладів, пошук площі під кривою за допомогою безлічі прямокутників - це Midpoint Rule, Правило середньої точки. Ця техніка вважається більш точною, оскільки за своїм визначенням усереднює значення.
Іншою технікою є пошук площі, розділяючи на трапеції. Така стратегія може здатися більш коректною, оскільки візуально трапеції краще вписуються під графік функції, ніж прямокутники, але Правило трапеції часто “занижує” значення. Відразу не можна на 100% сказати, яка техніка буде краще для того чи іншого інтегралу. Коректним буде знайти площу за обома техніками, потім знайти абсолютні та відносні похибки обох технік та обрати ту, де похибки менші.
Ці техніки нечасто зустрічаються, у шкільній та університетських програмах, тому раджу самостійно ознайомитися з ними.
Це все, дякую, що дочитали, і сподіваюся, комусь допомогла ця стаття. Не соромтеся залишати коментарі, якщо щось незрозуміло.
