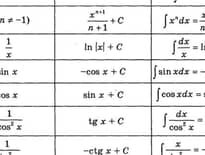
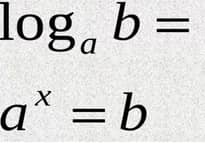Ґрунт, база і литосферна плита
Комплексна арифметика - це галузь математики, яка вивчає властивості та операції, що виконуються з комплексними числами. Комплексні числа складаються з двох частин: дійсної та уявної. Дійсна частина - це звичайне дійсне число, а уявна частина - це число, помножене на уявну одиницю (позначається як "і" або "j").
Крім того, комплексна арифметика має багато інших властивостей, таких як спряжене комплексне число, модуль комплексного числа, аргумент комплексного числа та інші.
Любий читачу, якщо тобі подобається подібні довгочити та ти хотів би побачити еволюцію цього проекту в майбутньому, то вподобай цю публікацію!
Також переглянь інші праці до яких я доклав немало зусиль:
Комплексні числа: Побудова та представлення у вигляді a + bi

Комплексна арифметика має широкі застосування в різних галузях науки та техніки, зокрема в електротехніці, фізиці, сигнальній обробці та теорії керування, що я вже встиг згадати в коментарях, де мені запропонували цю тему.
Комплексне число можна записати у вигляді z = a + bi, де "a" - дійсна частина, "b" - уявна частина, а "i" - уявна одиниця. Наприклад, комплексне число z = 3 + 2i має дійсну частину 3 та уявну частину 2.
У комплексній арифметиці можна виконувати операції додавання, віднімання, множення та ділення комплексних чисел. Наприклад, додавання двох комплексних чисел здійснюється шляхом додавання їх дійсних та уявних частин окремо. Цебто, наприклад: 3і+3+5-1і буде дорівнювати 2і + 8.
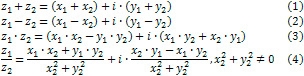
Спряжені комплексні числа
Комплексні числа є розширенням множини дійсних чисел, які складаються з дійсної та уявної частини. У дійсних числах неможливо вирішити деякі рівняння, наприклад, $x^2 = -1$, оскільки немає дійсного числа, яке має квадрат -1. Однак, такі рівняння можуть бути розв'язані за допомогою комплексних чисел.
Потреба в спряжених комплексних числах виникає з необхідності математичної моделі для розв'язування різних проблем. Спряженість є однією з властивостей комплексних чисел, яка має важливі застосування в алгебрі, геометрії та фізиці.
Формула спряження $\overline{z} = a - bi$ вказує, що спряжене комплексне число має таку саму дійсну частину, але з протилежним знаком, і таку саму уявну частину з протилежним знаком.
(дивитися картинку нижче)Наприклад, якщо маємо комплексне число $z = 2 + 3i$, то його спряжене число $\overline{z}$ обчислюється як $\overline{z} = 2 - 3i$.
![For z = 2 + 3i verify the following: i) [tex]\overline{\bar{z}} = z[/tex] ii) [tex]z\bar{z} = |z|^{2}[/tex] - Brainly.in](https://cdn.drukarnia.com.ua/643c7f1f1272bd9066a78201/images/articles/64b858a6280f44210206c1b5/TD-L1qbCd0PDqXCfNEz.jpeg)
Властивості спряжених чисел
Оригінал з усіма формулами та прикладами можна переглянути: https://studfile.net/preview/9794390/page:2/
1. Сума і добуток спряжених комплексних чисел є числа дійсні
2. Число, спряжене з сумою двох чисел, дорівнює сумі чисел, спряжених з доданками
3. Число, спряжене з добутком двох чисел, дорівнює добутку чисел, спряжених з співмножниками
4. Число, спряжене з різницею двох чисел, дорівнює різниці чисел, спряжених зі зменшуваним і від’ємником
5. Число, спряжене з часткою двох чисел, дорівнює частці чисел, спряжених з діленим і дільником
Правило віднімання комплексних чисел: для того, щоб відняти два комплексних числа
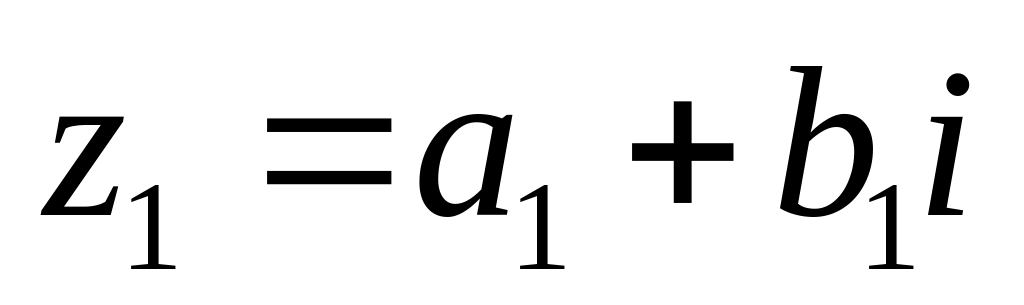
та

, потрібно окремо знайти різниці дійсної та уявної частин і результати відповідно записати, тобто
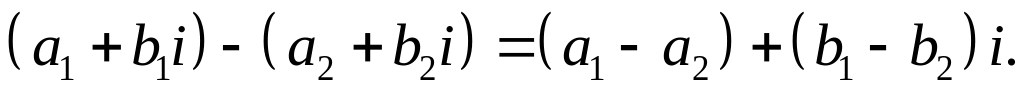
Правило ділення комплексних чисел: для того, щоб поділити два комплексних числа потрібно і чисельник, і знаменник отриманого дробу помножити на число, спряжене до знаменника, тобто числа, отже

Геометрична інтерпретація спряжених комплексних чисел
Спряжене комплексне число можна розглядати як точку у комплексній площині, яка знаходиться відповідно до оригінального числа відносно дійсної вісі. Геометрично, це відображення точок відносно вісі Re або Im.
Застосування спряжених чисел у векторних операціях та геометричних перетвореннях
Спряжені числа мають важливі застосування в векторних операціях і геометричних перетвореннях. Наприклад, при обчисленні скалярного добутку двох комплексних векторів, спряжене комплексне число використовується для зміни знаку уявної частини одного з векторів.
Висновки
Отже, поговоримо про ці спряжені комплексні числа. Якщо вам колись потрібно було вирішити рівняння з квадратом від'ємного числа, то ви вже знаєте, що звичайні дійсні числа не дають такої можливості. Але не хвилюйтесь, комплексні числа це зарішають.
Так от, одна з найцікавіших рис комплексних чисел - це їх спряженість. Ви можете отримати спряжене комплексне число, просто змінивши знак уявної частини. Це як знаходження відображення у дзеркалі, але для чисел!
Комплексні числа та їх спряженість - це чудовий світ математики. Спряжені числа отримуються заміною знаку уявної частини. Вони зберігають операції додавання та множення. Геометрично вони представляються як точки, симетричні відносно дійсної вісі. Спряжені числа мають застосування у векторних операціях та геометричних перетвореннях.
Розширюйте, покращуйте, вдосконалюйте, зміцнюйте український контент.
Слава Україні!