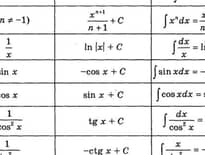
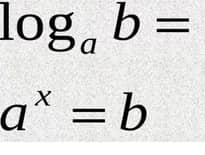Якщо щось незрозуміло, а це недивно,то звертайтися до мене в коменетарях! В НМТ майже нема завдань з векторами, проте ви маєте розуміти що таке коленіарність векторів, скалярний добуток, умови за яких вектори перпендикулярні та розуміння графіків(маю на увазі, вміння працювати з координатами). Основні формули є в довідкових, перегляньте приклади з ними та гляньте формулу кола.
Ця стаття написана більш глибоко, ніж шкільні вектори.
Введення до векторів: Основні поняття та властивості
Вектори є ключовим поняттям у математиці, фізиці та комп'ютерних науках. Вони дозволяють нам описувати та вимірювати фізичні величини, рухатися у просторі та вирішувати різноманітні завдання. В цьому розділі ми розглянемо основні поняття та властивості векторів.
1. Вектори як напрямлені величини: Вектори представляють собою напрямлені величини, які мають дві основні характеристики - напрямок та величину. Напрямок вектора вказує, в якому напрямку рухається величина, тоді як величина визначає його довжину або магнітуду.
2. Геометричне зображення векторів: Вектори можна представити у вигляді стрілок або ліній на графічному зображенні. Довжина стрілки відображає магнітуду вектора, а напрямок стрілки вказує на його напрямок.
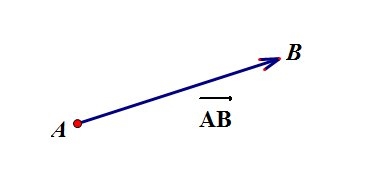
3. Компоненти вектора: Вектори можна представити у вигляді компонентів або координат. Наприклад, двовимірний вектор можна представити як (x, y), де x - компонента у горизонтальному напрямку, а y - компонента у вертикальному напрямку.

4. Додавання та віднімання векторів: Вектори можна додавати та віднімати, щоб отримати нові вектори. При додаванні векторів їх компоненти просто складаються, а при відніманні відповідні компоненти віднімаються.
5. Множення вектора на скаляр: Вектор можна помножити на число, відоме як скаляр. Це множення змінює магнітуду вектора, але не його напрямку.
6. Векторні операції та властивості: Вектори також підлягають іншим операціям, таким як скалярний добуток, векторний добуток, векторний проекція і т. д. Вони мають ряд властивостей, таких як комутативність, асоціативність та дистрибутивність, які дозволяють ефективно працювати з векторами.
Розуміння цих основних понять та властивостей векторів є важливим для подальшого вивчення та застосування цієї математичної концепції.
Операції з векторами: додавання, віднімання та множення на скаляр
Вектори можуть піддаватися різним операціям, які дозволяють нам комбінувати та маніпулювати ними. Основними операціями з векторами є додавання, віднімання та множення на скаляр. Давайте розглянемо кожну з цих операцій детальніше:
1. Додавання векторів:
Додавання векторів полягає у поелементному складанні їх компонентів. Якщо маємо два вектори, наприклад, A = (A₁, A₂, A₃) і B = (B₁, B₂, B₃), то їх сума (позначається як C) буде мати такі компоненти: C₁ = A₁ + B₁, C₂ = A₂ + B₂, C₃ = A₃ + B₃. Додавання векторів можна геометрично представити як переміщення одного вектора вздовж іншого.
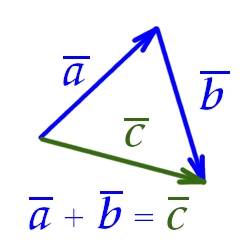
2. Віднімання векторів:
Віднімання векторів полягає у поелементному відніманні їх компонентів. Якщо маємо два вектори, A = (A₁, A₂, A₃) і B = (B₁, B₂, B₃), то їх різниця (позначається як C) буде мати такі компоненти: C₁ = A₁ - B₁, C₂ = A₂ - B₂, C₃ = A₃ - B₃. Віднімання векторів також можна геометрично інтерпретувати як переміщення одного вектора протиоповідно до іншого.

3. Множення вектора на скаляр:
Множення вектора на скаляр полягає у множенні кожної компоненти вектора на задане число. Якщо маємо вектор A = (A₁, A₂, A₃) та скаляр k, то множення на скаляр дозволяє отримати новий вектор C = (C₁, C₂, C₃), де C₁ = k * A₁, C₂ = k * A₂,
C₃ = k * A₃. Ця операція змінює магнітуду вектора, але не його напрямок.
Операції додавання, віднімання та множення на скаляр є основою для багатьох інших векторних операцій та застосувань. Вони дозволяють нам комбінувати вектори, змінювати їх масштаб та виконувати різні обчислення в контексті векторного простору.
Скалярний добуток: визначення та його застосування
Скалярний добуток є однією з основних операцій з векторами, яка виконується між двома векторами того ж розміру. Він дозволяє отримати скалярне (числове) значення, необхідне для різних обчислень та аналізу. Давайте розглянемо визначення скалярного добутку та його застосування.

Визначення:
Скалярний добуток двох векторів A і B, позначений як A • B, обчислюється як сума покоординатних добутків їх компонентів. Для векторів A = (A₁, A₂, A₃) та B = (B₁, B₂, B₃) скалярний добуток визначається наступним чином: A • B = A₁ * B₁ + A₂ * B₂ + A₃ * B₃.
Застосування:
1. Визначення куту між векторами: Скалярний добуток може бути використаний для обчислення кута між двома векторами. Використовуючи теорему косинусів, можна встановити зв'язок між скалярним добутком векторів, їх довжиною та косинусом кута між ними.
2. Визначення проекції вектора: Скалярний добуток може бути використаний для обчислення проекції одного вектора на інший. Проекція вектора A на вектор B дорівнює добутку довжини вектора A на косинус кута між ними: projₐB = |A| * cos(θ), де θ - кут між векторами A і B.
3. Робота та енергія: Скалярний добуток використовується в фізиці для обчислення роботи, яку сила виконує на тіло вздовж шляху. Робота дорівнює добутку модулів сили та переміщення, помноженому на косинус кута між ними.
4. Ортогональність: Два вектори вважаються ортогональними, якщо їх скалярний добуток дорівнює нулю. Це властивість, яка має велике значення у векторній алгебрі та геометрії.
5. Обчислення елементів матриць: Скалярний добуток може бути використаний для обчислення елементів матриць, зокрема, використовується при множенні матриць та векторів.
Любий читачу, якщо тобі подобається подібні довгочити та ти хотів би побачити еволюцію цього проекту в майбутньому, то вподобай цю публікацію!
Також переглянь інші праці до яких я доклав немало зусиль:
Векторний добуток: властивості та геометричне інтерпретування
Векторний добуток: властивості та геометричне інтерпретування
Векторний добуток є ще однією важливою операцією з векторами. Він виконується між двома векторами того ж розміру і дає вектор, перпендикулярний до площини, утвореної цими векторами. Розглянемо властивості векторного добутку та його геометричне інтерпретування.
Властивості векторного добутку:
1. Ортогональність: Векторний добуток двох векторів завжди перпендикулярний до площини, утвореної цими векторами. Це означає, що векторний добуток A × B буде ортогональним до векторів A і B.
2. Напрям: Напрям векторного добутку визначається за правилом правої руки. Якщо ви праву руку положите так, щоб вказівний палець вказував у напрямку вектора A, а середній палець - в напрямку вектора B, то великий палець покаже напрям векторного добутку A × B.
3. Величина: Величина векторного добутку обчислюється за формулою |A × B| = |A| * |B| * sin(θ), де θ - кут між векторами A і B. Вона рівна площі паралелограма, утвореного векторами A і B.
Геометричне інтерпретування векторного добутку:
Геометрично, векторний добуток використовується для визначення напряму та величини нормального вектора до площини, утвореної двома векторами. Він може бути використаний для різних застосувань, таких як:
1. Обчислення площі трикутника: Площа трикутника, утвореного двома векторами, може бути обчислена як половина величини їх векторного добутку.
2. Визначення нормалей до поверхні: Векторний добуток використовується для визначення нормалей до поверхонь у тривимірному просторі. Нормаль до площини може бути отримана шляхом обчислення векторного добутку двох нележачих на ній векторів.
3. Механіка: Векторний добуток використовується в механіці для обчислення моменту сили (моменту обертання) і моменту імпульсу.
4. Електродинаміка: Векторний добуток між векторами електричного поля та магнітного поля використовується для отримання вектора Пойнтинга, який вказує напрямок та потужність електромагнітної хвилі.
Векторний добуток є потужним інструментом, який знаходить широке застосування у фізиці, геометрії, комп'ютерній графіці та багатьох інших областях.
Ортогональність та лінійна незалежність векторів
Ортогональність векторів: Два вектори називаються ортогональними, якщо їх скалярний добуток дорівнює нулю. Ортогональні вектори перпендикулярні один до одного і лежать в одній площині. Геометрично це означає, що вектори утворюють прямий кут між собою.
Лінійна незалежність векторів: Набір векторів є лінійно незалежним, якщо ніяка комбінація цих векторів (крім тривіальної комбінації, де всі коефіцієнти дорівнюють нулю) не дає нульового вектора. Це означає, що ні один вектор з набору не може бути виражений як лінійна комбінація інших векторів. Геометрично це означає, що вектори не лежать на одній прямій (для двох векторів) або в одній площині (для трьох векторів).
Взаємозв'язок: Якщо набір векторів є ортогональним, то він також є лінійно незалежним, і навпаки. Однак, важливо зазначити, що лінійна незалежність не завжди означає ортогональність, і навпаки.
Ортогональність векторів дає зручність при обчисленнях, оскільки спрощує скалярний добуток та інші операції. Лінійна незалежність векторів є важливою властивістю у лінійній алгебрі та математичній моделюванні.
Знання про ортогональність та лінійну незалежність векторів дозволяє розуміти та вирішувати різні задачі, пов'язані з аналізом та маніпуляціями з векторами у різних областях, таких як фізика, геометрія, комп'ютерна графіка, машинне навчання та інші.
Проекція вектора: визначення та геометричне значення
Проекція вектора - це процес визначення компоненти вектора, яка спрямована вздовж певного напрямку або на певну пряму. Це дозволяє розкласти вектор на дві складові: проекцію на заданий напрямок та ортогональну компоненту, яка перпендикулярна до цього напрямку.
Визначення проекції вектора: Проекція вектора A на напрямок вектора B обчислюється за допомогою скалярного добутку векторів: projB(A) = (A·B / |B|) * (B / |B|), де projB(A) - проекція вектора A на напрямок вектора B.
Геометричне значення проекції: Геометрично проекція вектора може бути інтерпретована як довжина відрізка, який сполучає точку початку вектора з його проекцією на заданий напрямок. Проекція вектора A на напрямок B вказує, яка частина вектора A спрямована вздовж напрямку B.
Геометрично, проекція вектора може бути позначена як відрізок на прямій або вектор, що лежить на цій прямій. Проекція може мати як позитивне, так і негативне значення, залежно від того, в якому напрямку розташована проекція відносно точки початку вектора.
Проекція вектора є важливим поняттям в геометрії, фізиці та інших науках. Вона знаходить застосування у вирішенні різних завдань, таких як розрахунки сили, руху тіл, обробка сигналів, комп'ютерна графіка та багато інших областей.
Розширюйте, покращуйте, вдосконалюйте, зміцнюйте український контент.
Слава Україні!