Вступ
Використання інтегралу дуже розповсюджене в багатьох наукових галузях, таких як фізика, економіка, інженерія та біологія. Він також знаходить застосування в різних сферах, таких як обробка сигналів, аналіз даних та машинне навчання.
Навчитися використовувати інтеграл може бути складним, але варто зрозуміти його основні принципи, щоб бути успішним у своїй професійній діяльності. Якщо ви зацікавлені в математиці, вивчення інтегралу може бути захоплюючою та корисною пригодою.
Будь ласка, витрати трохи свого часу. Ця стаття справді поможе більше розібратися тобі в цій темі.
Види інтегралів
Насправді, їх доволі багато. Я перелічу їх нижче, але розбирати будемо тільки перші два. Тому що інші використовуються вже в якихось окремих галузях, а перші два, цебто неозначений інтеграл та визначений інтеграл, проходять в 11 класі школи.
Невизначений інтеграл | Якщо функція F(x) — первісна для функції f(x), то множина функцій F(x)+C (де C — довільна стала) називається невизначеним інтегралом від функції f(x), позначається символом ∫f(x)dx і пишеться ∫f(x)dx=F(x)+C. |
|---|---|
Визначений інтеграл | інтеграл, який має верхню та нижню межу і обчислює площу під кривою функції для певного діапазону. Визначений інтеграл позначається як "ₐ∫ᵇabf(x)dx", де a та b - це верхня та нижня межі відповідно. |
Двійковий інтеграл | інтеграл, який використовується для обчислення об'єму тіла між двома поверхнями, за умови, що їх можна виразити як функції двох змінних. Двійковий інтеграл позначається як "ₐ∫ᵇₑ∫ᵈRf(x,y)dxdy", де R - область, що розглядається. |
Трійковий інтеграл | інтеграл, який використовується для обчислення об'єму тіла, яке знаходиться між поверхнею та площиною. Трійковий інтеграл позначається як "ₐ∫ᵇₑ∫ᵈᵢ∫ʰWf(x,y,z)dxdydz", де W - об'єм, що розглядається. |
Інтеграл Фур'є | інтеграл, який використовується в аналізі сигналів для розкладання сигналу на складові частини з різними частотами. Інтеграл Фур'є позначається як "∫-∞∞f(x)e^(-iωx)dx |
Невизначений інтеграл
Множина всiх первiсних функцiй для функцiї f(x) називається невизначеним iнтегралом i позначається ∫f(x) dx.
Тут f(x) називається пiдiнтегральною функцiєю, f(x)dx називається пiдiнтегральним виразом, x — змiнна iнтегрування, dx — диференцiал змiної iнтегрування. Таким чином, якщо функцiя F(x) є первiсною для функцiї f(x), тодi ∫ f(x) dx = F(x) + C. Тут C — довiльна стала, яка називається сталою iнтегрування.
Не зроз цю теорію? То зараз розберемо на прикладах!
∫ f(x) dx = F(x) + C - це є нашею основною формулою. Все що нам тре, так це табличні значення. Якщо ти збиражшся здавати(здав) ЗНО\НМТ, то вже знаєш, що ця інформція є в довідковому матеріалі. Це таблиця первісних ( ті, шо F(x) ), ось:

Перший стовпчик це твоя функція, що знаходиться під інтегралом. Як виглядає сам інтеграл з цією функцією ти можеш побачити в третьому стовпчику. А другий і є наша відповідь.
Як бачиш, то все що треба - розуміння цієї таблиці.
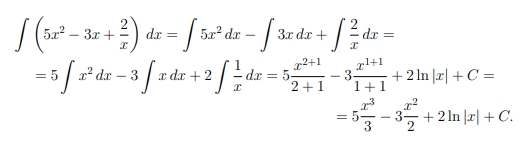
1) Інтеграл від суми двох функцій дорівнює сумі відповідних інтегралів: ∫(f(x) + g(x)) d x = ∫ f(x) d x + ∫ g (x) d x
2) Інтеграл від різниці двох функцій дорівнює різниці відповідних інтегралів: ∫(f(x) − g(x)) d x = ∫ f(x) d x − ∫ g (x) d x
3) Константу можна виносити за знак інтеграла: ∫ C f(x) d x = C ∫ f(x) d x
Визначений інтеграл
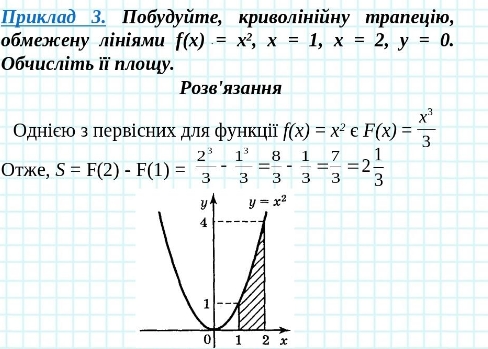
Геометричний зміст визначеного інтеграла — це площа криволінійної фігури (криволінійної трапеції), обмеженої віссю абсцис, двома вертикалями на краях відрізка і кривою графіка функції.
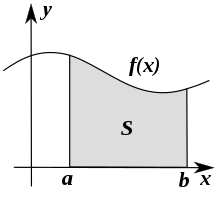
Знаєш як її контрити? А дуже легко. Щоб знайти площу криволінійної трапеції, нам тре використати формулу Лейбніца:

Якщо у тебе нема криволінійної трапеції, то просто розбиваєш свій визначений інтеграл на кілька невизначених, як я казав вище, та вирішуєш
1) Інтеграл від суми двох функцій дорівнює сумі відповідних інтегралів: ∫(f(x) + g(x)) d x = ∫ f(x) d x + ∫ g (x) d x
2) Інтеграл від різниці двох функцій дорівнює різниці відповідних інтегралів: ∫(f(x) − g(x)) d x = ∫ f(x) d x − ∫ g (x) d x
3) Константу можна виносити за знак інтеграла: ∫ C f(x) d x = C ∫ f(x) d x
Практика привище за все
Так, тепер, коли ми ознайомилися з однією необхідною формулою та зрозуміли як працює невизначений інтеграл, ми легко можемо вирішити подібні задачі:
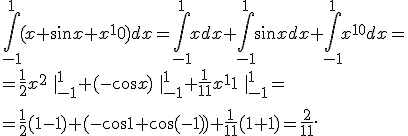
Я вкладую доволі багато часу в усі свої праці, тож напишіть відгук.
