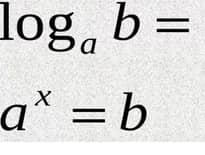Все ще вважаєш, що похідна складна і незрозуміла тема? Або просто хочеш повторити? Тоді цей довгочит було написано для тебе.
Ліміт(lim)
Ліміт - це поняття, що використовується в математиці для опису поведінки функцій або послідовностей, коли аргумент або член послідовності наближається до певної точки. Ліміт дозволяє нам визначити значення, до якого функція або послідовність збігаються або наближаються, незалежно від фактичного значення в точці.
lim (x→a) f(x) = L
або
lim (n→∞) a_n = L
Ліміти можуть бути визначені як для точок на числовій прямій (наприклад, наближення до певного числа) так і для нескінченності (набігання на нескінченність).
Ліміти використовуються в багатьох галузях математики, таких як аналіз, диференціальне рахування, інтегралі, теорія ймовірностей та інші. Вони дозволяють нам досліджувати властивості функцій, визначати їх неперервність, збіжність, диференційовність та інші характеристики.
Приклад ліміту

Особисто я не бачу нічого складного. Як правило, то треба просто підставляти число, до якого наближається х
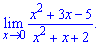
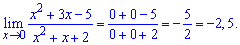
Як бачите, нічого складного в тому немає. До того ж, я ще не зустрічав цієї теми десь, окрім 10го класу.
Любий читачу! Якщо тобі цікава тема математика, то напелегливо раджу ознайомитися з цими постами:
Похідна
Похідною функціїї y=f(x) у точці х0 називається границя відношення приросту функції до приросту аргументу, коли приріст аргументу прямує до нуля.
Геометричний зміст похідної
Уявімо собі графік функції на координатній площині. Кожна точка на графіку відповідає певному значенню аргументу та значенню функції у цій точці. Геометрично, похідна визначає нахил тангенти до графіку функції у кожній її точці.
Геометрично, похідна відповідає нахилу прямої, яка найкраще наближається до графіку функції у даній точці. Ця пряма називається тангентою. Наклон тангенти вказує на швидкість зміни значення функції у цій точці.
Якщо похідна додатня, то функція зростає у цій точці. Це означає, що нахил тангенти вгору, і значення функції збільшується при збільшенні аргументу. Якщо похідна від'ємна, то функція спадає у цій точці, нахил тангенти спрямований вниз, і значення функції зменшується при збільшенні аргументу.
Коли похідна дорівнює нулю, то маємо точку екстремуму - максимуму або мінімуму функції. В цій точці тангента горизонтальна, і значення функції не змінюється при невеликому зміщенні аргументу.
Таким чином, геометрично похідна вказує на швидкість зміни функції та характер руху на графіку. Вона дозволяє нам аналізувати поведінку функції та визначати різні властивості, такі як мінімуми, максимуми, точки перегину тощо.
Як обчислювати похідну(теорія)
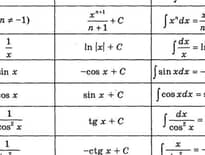
Знизу буде таблиця похідних фунцій. Все що вам потрібно буде робити, це брати ваш приклад, потім подивитися яка це функція за цією таблицею та взяти похідну, як вказано нижче.

Ось декілька прикладів рівнянь похідної для різних видів функцій:
Лінійна функція: f(x) = ax + b f'(x) = a
Квадратична функція: f(x) = ax^2 + bx + c f'(x) = 2ax + b
Логарифмічна функція: f(x) = ln(x) f'(x) = 1/x
Синусоїдальна функція: f(x) = sin(x) f'(x) = cos(x)
Косинусоїдальна функція: f(x) = cos(x) f'(x) = -sin(x)
Це доволі легкі приклади. Тепер, коли ви маєте розуміння того, як це робити, ми можемо роздивитися більш складні приклади
Як обчислювати похідну(приклади)
Припустимо вам дали функцію:
x⁵-4x³+2x²-7x
Це буде звичайна квадратична функція. Тож ми пам’ятаємо, що за таблицею хⁿ=nxⁿ⁻¹ , тож тепер підставимо наш приклад під цю формулу та отримаємо:

Тепер пропоную розглянути ще один приклад. Вам дали функцію:
y=(1+x²)\(1-x²)
Тут нам вже тре буде ділити одну похідну на іншу. Ми застосуємо ось ці формули:
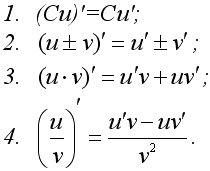
Нам буде потрібна 4 формула.
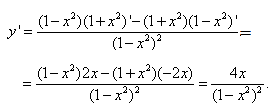
Як бачите, тепер ми просто підставляємо наші значення під формулу, потім просто дивимося в таблицю та підставляємо похідну від функції.
Спробуй вмрішити це сам(-а): у=(х²+3х-1)\(х³+4х)
Дотична
Рівняння дотичної до кривої y=f(x) у точці M(x0;y0) є:
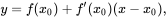

Дотична до графіку функції визначається як пряма, яка торкається графіку у певній точці і має той же нахил, що й графік у цій точці. Дотична є найближчою лінією до графіку у цій точці.
Для знаходження рівняння дотичної до графіку функції використовуються два основні кроки:
Знайдіть похідну функції у заданій точці, вирахувавши значення похідної f'(x0).
Використовуйте знайдене значення похідної та задану точку (x0, f(x0)), щоб скласти рівняння дотичної у формі y - f(x0) = f'(x0)(x - x0).
Це рівняння вказує, що різниця між значеннями y координати на графіку функції та значенням f(x0) в точці x0 дорівнює добутку значення похідної f'(x0) та різниці між значеннями x координати на графіку та значенням x0.
Таким чином, рівняння дотичної в точці (x0, f(x0)) має вигляд y - f(x0) = f'(x0)(x - x0).
Рівняння дотичної використовується для наближеного опису графіку функції в околі точки x0 та дозволяє вивчати поведінку функції навколо цієї точки, включаючи нахил та кут нахилу графіку.
Приклад:
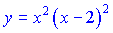

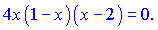


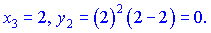
Висновок
Підсумовуючи наш довгочит "Похідна та ліміти: Основи та застосування" можна зробити наступні висновки:
Ліміт є важливим поняттям в математиці, яке дозволяє аналізувати поведінку функції наближаючись до певної точки. Визначення ліміту дозволяє обчислити значення функції в тій точці або визначити її поведінку при наближенні до цієї точки.
Похідна функції вказує на швидкість зміни функції в кожній точці. Вона може бути обчислена за допомогою різних методів, включаючи диференціальні правила, геометричну інтерпретацію та чисельні методи.
Дотична до графіку функції є прямою, яка торкається графіку у певній точці і має той же нахил, що й графік у цій точці. Рівняння дотичної можна скласти, використовуючи значення похідної функції в цій точці та координати точки на графіку.
Знання ліміту, похідної та дотичної дозволяє аналізувати та розуміти властивості функцій, їх поведінку, максимуми та мінімуми, а також наближено апроксимувати значення функції в околі певної точки.
Розширюйте, покращуйте, вдосконалюйте, зміцнюйте український контент.
Слава Україні!