Більшість туторіалів по даній темі містять дуже мало теорії, або не містять її взагалі та використовують 1 - 2 найпопулярніші моделі. Ця стаття присвячена теорії, простим та більш складним методам аналізу та прогнозування часових рядів. Я розділила матеріал на умовні три частини - легку, середню та складну, бо ключ до розуміння - це починати з основ.
Введення до часових рядів
Що таке часовий ряд? Це зміна кількості корму, який їсть ваша кішка або собака, від часу. Це коливання ціни акцій корпорацій, показання температури на весь день, зміна смаку чаю з часом. Як зрозуміти та правильно обробити часовий ряд?
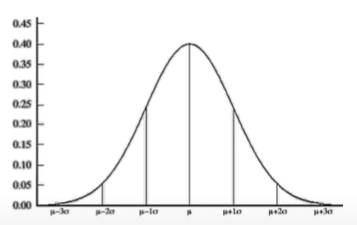
Основна відмінність між часовим рядом і окремими експериментами, які можна зобразити за допомогою гістограми в тому, що кожна точка (змінна) у часовому ряді віддалена від наступної точки на однакову відстань та може залежати від попередньої (автокореляція).
Що можна зробити з часовим рядом та чому він такий корисний?
Часовий ряд дає можливість передбачити значення наступної (майбутньої) точки (змінної), наприклад, передбачити ціну акції через годину, день, тиждень, базуючись на розмірності даних. Але регресія робить теж саме, хіба ні? Саме в цьому аспекті і лежить основна відмінність. Результатом регресії є кількісна оцінка впливу незалежних змінних на процеc, тоді як часовий ряд можна відтворити шляхом розкладання, не розраховуючи вплив кожної змінної, тобто не “заглядаючи під капот”. Ряд складається з двох частин - сигналу та шуму. Сигнал - це математично залежні змінні, які можна проаналізувати та прибрати з часового ряду. Шум навпаки складається з рандомних значень, частіше за все нормального розподілу, та візуально схожий на звуковий шум.
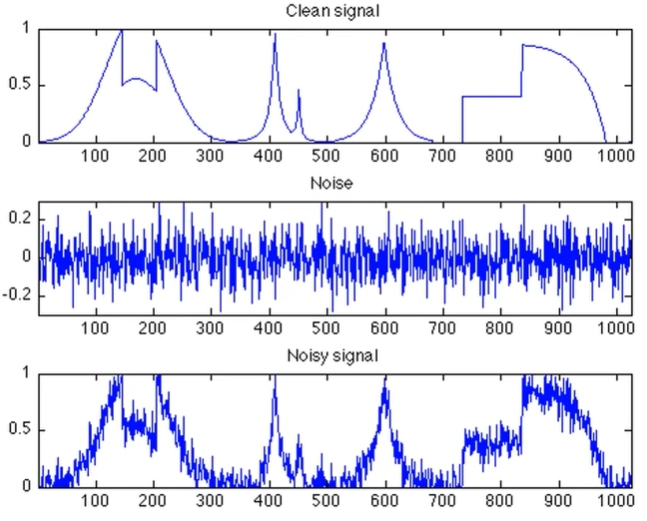
Реальні дані є поєднанням шуму та сигналу і найчастіше за все низька якість моделі залежить саме від неможливості відтворити (передбачити) шум.
Патерни сигналу:
Сезонність (seasonality) - циклічні коливання змінної в залежності від часу. Наприклад, зниження температури взимку.
Тренд (trend/level) - це наклон ряду до горизонтальної осі. Тренд може бути зростаючим або спадаючим, якщо тренд не змінюється, то часовий ряд розташований горизонтально.
Автокореляція - це “пам’ять” ряду, значення змінної в конкретний час напряму залежить від попередніх значень змінної .
Якщо ряд не містить патерни, його називають стаціонарним. Стаціонарним (Stationary) є ряд без тренду та сезонності, середнє та стандартне відхилення якого є константами. Окремим патерном є часові ряди, які не можна зробити стаціонарними, прибравши тренд та/або сезонність. Такі ряди називають difference - stationary.
У цьому відео більш детально можна послухати про часові ряди.
Навчання якісної моделі для моделювання та прогнозування часового ряду це довгий та кропіткий процес. Алгоритм підготовки ряду залежить від вибору моделі, датасету та може містити базову очистку даних (нормалізацію), feature extraction та алгоритми приведення ряду до стаціонарного. У наступних пунктах я детально розповім про підготовку ряду для різних алгоритмів. Для деяких моделей високу якість можна досягти і без очистки часового ряду, для інших треба робити всі перелічені вище методи очистки.
Датасет та передмова
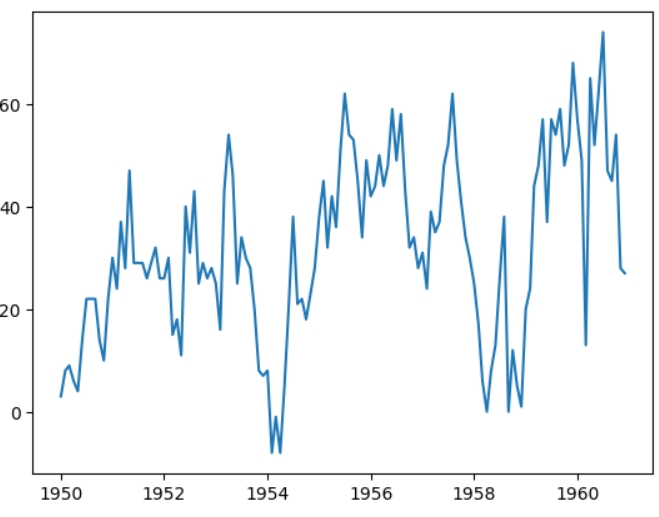
Стаття вийшла більша за розмірами, ніж очікувала, тому весь код можна знайти у цьому ноутбуці, містить коментарі англійською, але планую перекласти на українську. Як навчальні дані буду використовувати цей датасет, який виглядає наступним чином:
Датасет показує кількість пасажирів впродовж 1949 - 1960 років, щомісяця.
Аналіз часового ряду
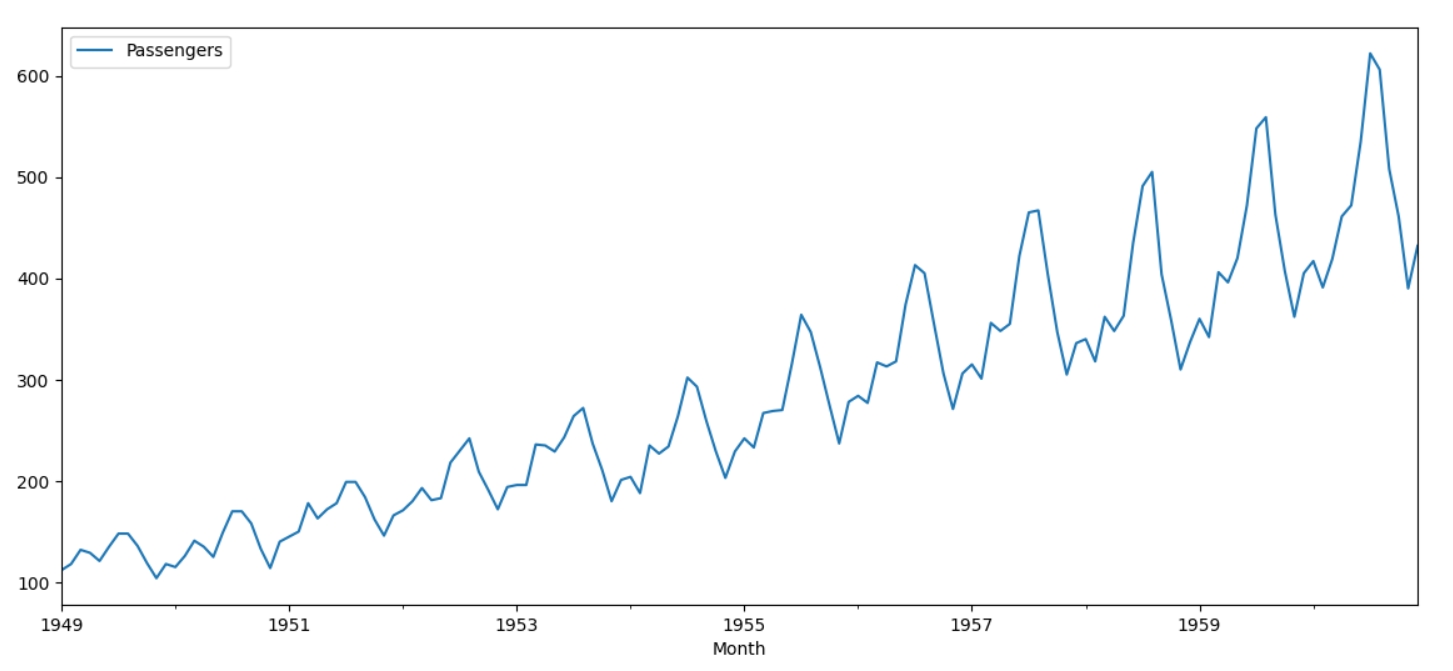
Почну з тих методів, які використовуються для аналізу багатьох видів даних.
Визначення розподілу
Для визначення розподілу використовують гістограму, Dataframe має вбудований метод hist().
df.hist()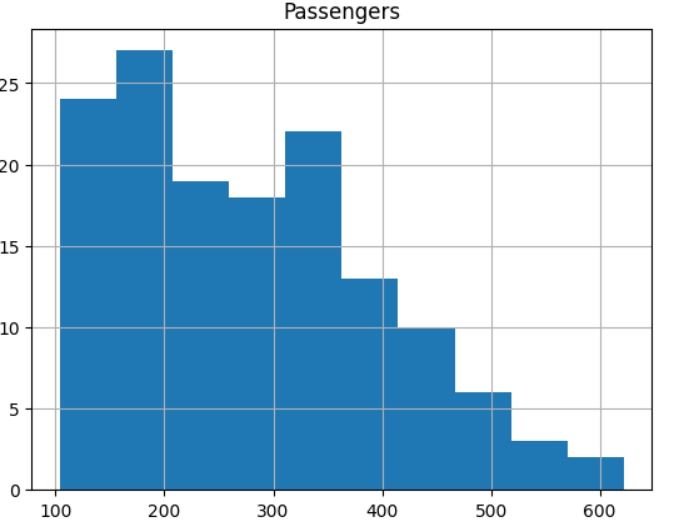
Часовий ряд має розподіл, відмінний від нормально, що звужує коло методів, які можна використати для нормалізації даних до одного, а саме до MinMaxScaler. З математичної точки зору такий розподіл сигналізує про те, що часовий ряд, скоріш за все, не є стаціонарним.
Викиди (Outliers)
Викиди - це дані, які “виділяються” з загальної купи, можуть бути або дуже маленькими, або дуже великими, порівняно з найближчою точкою. Вони впливають на якість більшості моделей машинного навчання та на вибір функції втрат.
Найпростіший спосіб, але не завжди дієвий, перевірити, чи є викиди - це подивитися на гістограму. Наприклад, якщо б стовпчик між 500 та 600 не містив даних (був би білим), можна було б припустити, що стовпчик 600 це викиди. Більш дієвий візуальний спосіб - це використати sns.boxplot:
sns.boxplot(df.Passengers)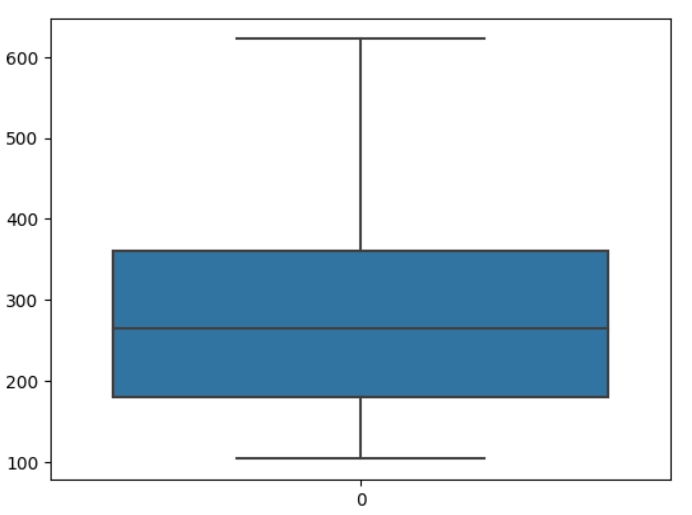
Вигляд boxplot підтверджує, що дані не мають викидів - вертикальна ось не містить чорних точок, які позначають викиди.
Перевірка на NAN
NAN - це неідентифікований тип даних, який не відображається на boxplot та забруднює дані. Значення такого типу потрібно видаляти, оскільки більшість алгоритмів машинного навчання не вміють працювати з ними. Разом з кількістю NAN значень виведу статистичні дані.
print(df.describe())
print("NAN values:",df.isna().sum())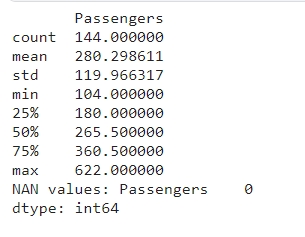
Що ж, прекрасно! Ряд не має NAN значень - однією проблемою менше.
Сезонність, тренд та шум
Подивіться на ілюстрацію знизу, як швидко ви знайдете тренд та сезонність? Я впевнена, що за пару секунд.
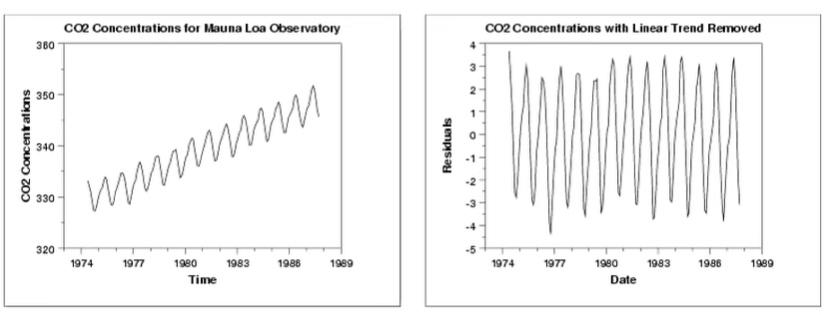
Стаціонарний часовий ряд легше передбачити, оскільки тренд є константою, на відміну від нестаціонарного часового ряду, чий тренд може змінити подія (наприклад, акції Твіттера впали через висловлювання Ілона Маска), передбачити яку дуже складно.
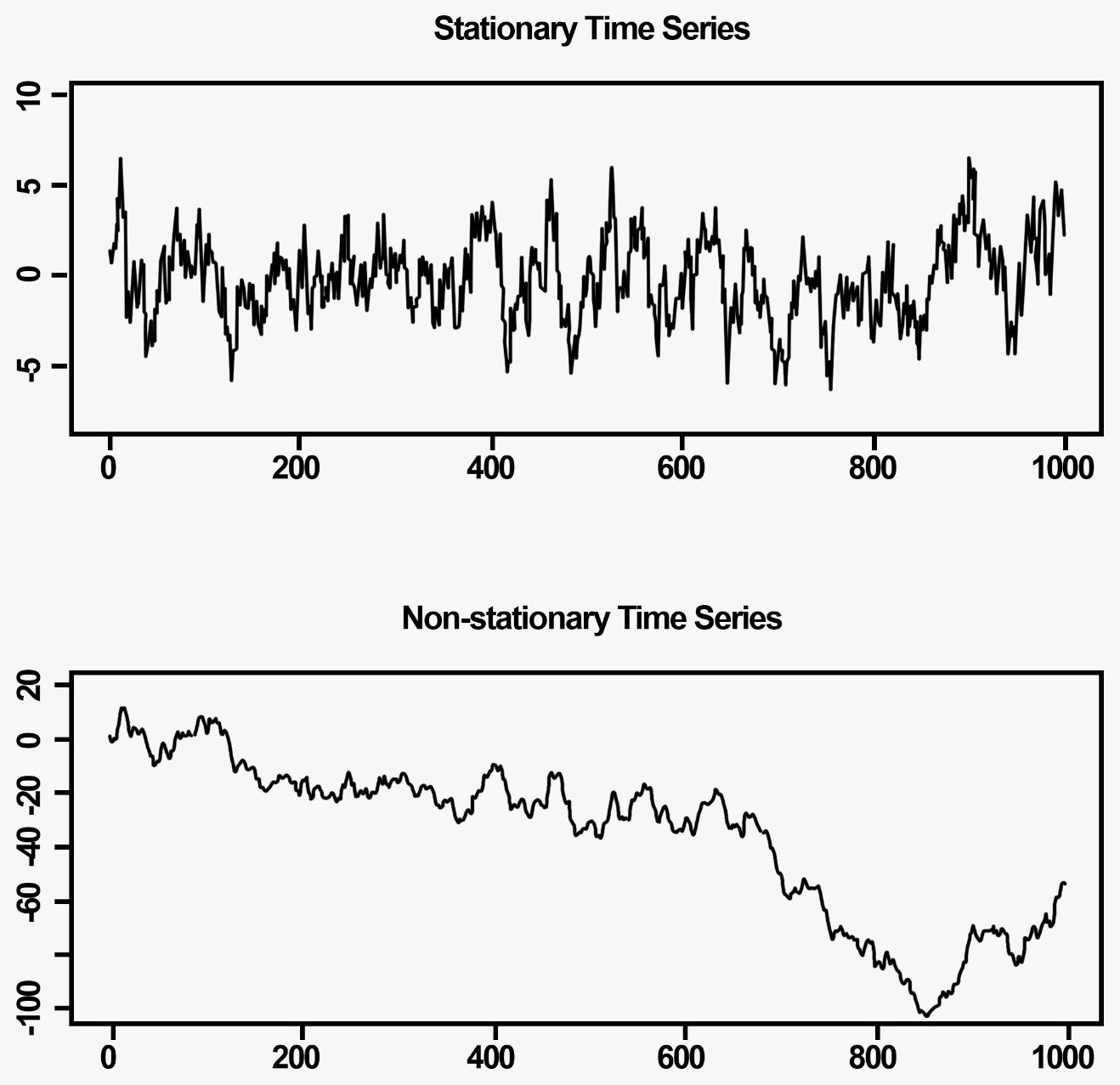
Розуміння тренду, сезонності та шуму є ключовим для розуміння часового ряду. Найпростішим способом знайти їх є statsmodels.tsa.seasonal.
from statsmodels.tsa.seasonal import seasonal_decompose
decomposed = seasonal_decompose(df['Passengers'])
decomposed.plot()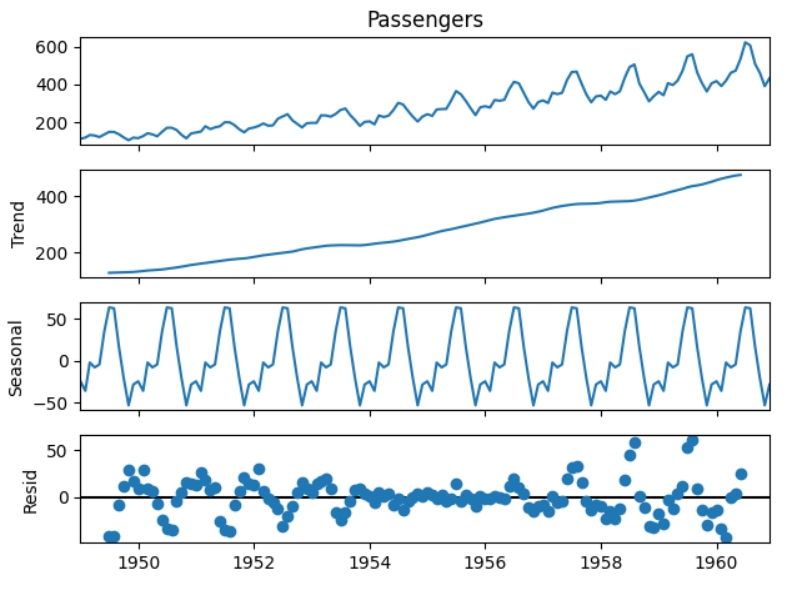
Тренд є майже лінійним та зростаючим. Це добре, бо лінійний тренд простіше передбачити, ніж нелінійний. Сезонність є однаковою та повторюється кожного року. Шум (resid) - це часовий ряд після прибирання з нього тренду та сезонності. Для цього часового ряду від доволі сильний, що може знизити якість прогнозування . Розглянемо сезонність на прикладі одного року.
df_month=df.copy()
df_month["Month"]=[d.strftime('%b') for d in df_month.index]
plt.figure(figsize=(20,10))
sns.boxplot(x=df_month["Month"],y=df_month["Passengers"])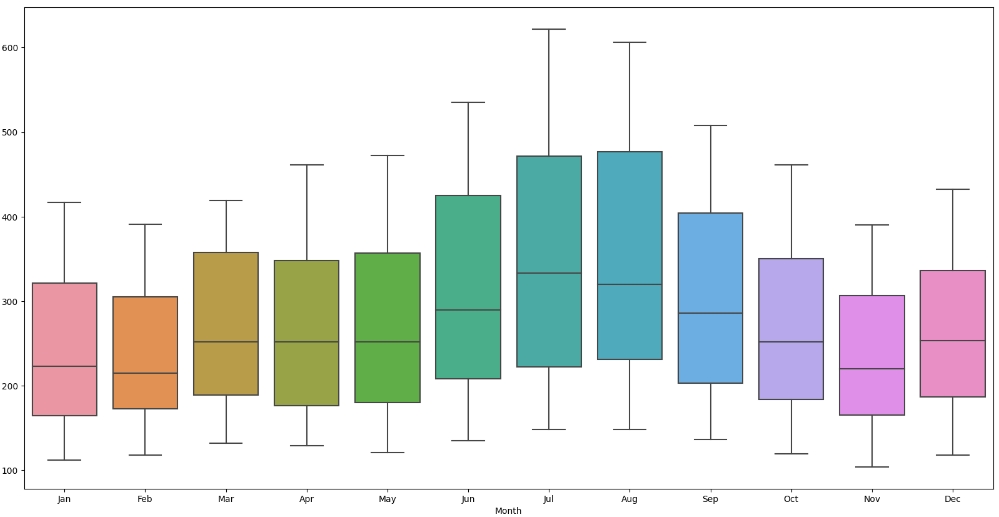
Кількість пасажирів збільшується впродовж двох літніх місяців та спадає після серпня. Одна з причин - люди летять на відпочинок влітку.
Наступні перевірки роблять тільки для часових рядів.
Доповнений тест Дікі - Фуллера (ADF)
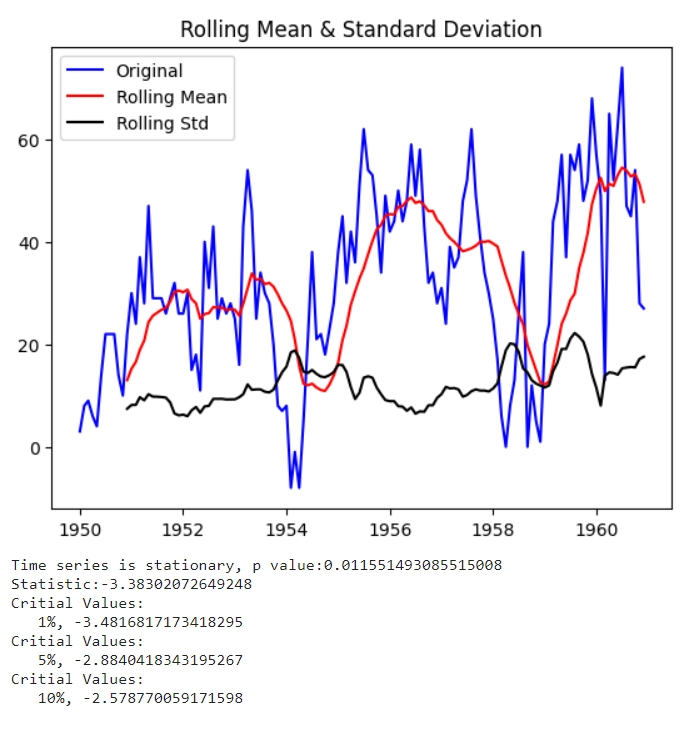
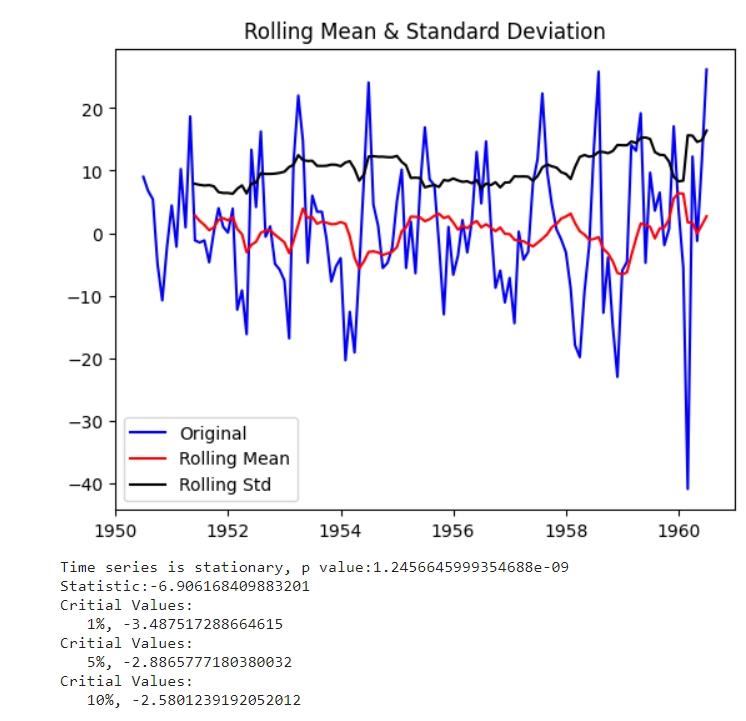
Тест ADF - це тест для перевірки стаціонарності часового ряду на основі unit root - це процес, який через диференціювання визначає чи є часовий ряд стаціонарним. Тест працює за принципом приймання або відкидання нульової гіпотези, яка полягає у тому, що ряд не є стаціонарним. Приймати чи відкидати нульову гіпотезу вирішується за значенням p (вірогідність неправильності нульової гіпотези): якщо значення є більшим за визначену константу, то нульова гіпотеза приймається (ряд не є стаціонарним), якщо меншим - гіпотеза відкидається (ряд є стаціонарним). Традиційно, константа = 0.05 (5%), але може бути іншою, в залежності від даних та моделі. Також важливо дивитися і на значення статистики, якщо воно більше за будь-яке критичне значення, то часовий ряд не є стаціонарним.
Реалізація наведеної нижче функції у 13 ячейці.
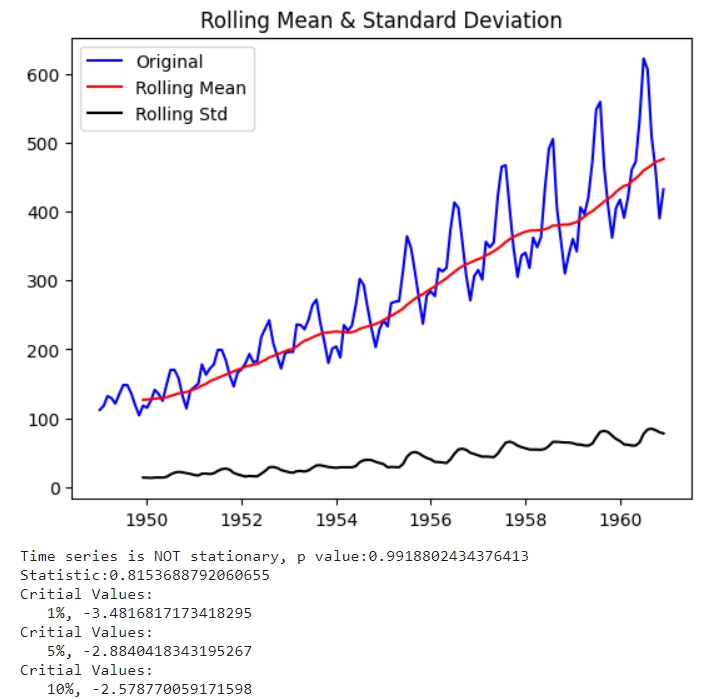
Rolling mean - це середнє значення точок часового ряду, і так, воно повторює лінію тренду. Rolling std - це значення дисперсії точок ряду. Простими словами - чим більша дисперсія, тим більше “розпилення даних”. Чим менші “хвилі” (див. на 1950 рік) - тим менше дисперсія, чим більші хвилі - тим більша дисперсія (див. на 1960 рік). Одразу можна припустити, що з роками дисперсія буде ставати все більше.
І останній пункт
Автокореляція
Кореляція - це зв’язок змінних між собою, автокореляція - зв’язок змінної з власними попередніми значенням. Оскільки ряд має тільки одну змінну - кількість пасажирів, аналізувати потрібно тільки автокореляцію. Перед тим, як графік автокореляції розкриється у всій красі, розкажу про поняття lags (лаги) - це значення змінної n - кількість часу назад, оскільки розмірністю мого часового ряду є місяць, то lag -1 означає значення 1 місяць тому для поточної змінної, -2 - два місяці тому, тощо. На наведеному нижче графіку кількість лагів дорівнює 4.
from statsmodels.graphics.tsaplots import plot_acf
plot_acf(df,lags=4)
plt.show()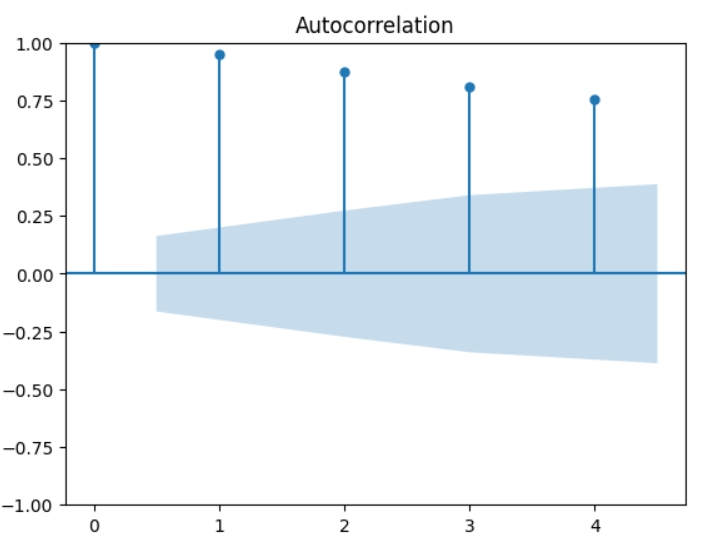
1 стовпчик (0) - це автокореляція значення з самим собою та завжди буде дорівнювати 1, 2 стовпчик (1) - це автокореляція поточного значення зі значенням місяць назад, тощо. Блакитний конус - це 95% інтервал, тобто все за межами конусу є скоріш за все кореляцією, а не статистичною помилкою. Часовий ряд має сильну кореляцію, що може призвести до збільшення bias. Якщо модель має high bias - це недонавчена модель, якщо модель має high variance - це перенавчена модель.
Все, зі статистикою покінчено, переходимо до простих методів декомпозиції часового ряду, щоб зробити ряд стаціонарним.
Декомпозиція часового ряду
Декомпозиція - це процес перетворення нестаціонарного часового ряду у стаціонарний шляхом прибирання з нього сезонності та тренду. Одразу зазначу, декомпозицію потрібно робити тільки для деяких моделей, наприклад регресійних, таких як ARIMA/SARIMA, моделі як LSTM/GRU, XGBoost, Prophet настільки потужні, що обробляють нестаціонарний ряд. Існують бібліотеки, які можуть декомпозувати ряд в одну строку, але не мають зворотньої функції для реконструкції. Реконструкція часового ряду - це процес зворотнього додавання до ряду тренду та сезонності, якщо цього не зробити, ряд буде паралельним осі х та буде мало корисним як прогнозування.
Deseasonality (моделювання сезонності)
Для того, щоб прибрати сезонність, найчастіше використовують різницю (differencing) між конкретним значенням змінної (Y) у конкретний час (t) за наступною формулою:
Yt = Yt - Yt-n, n - це показник сезонності. Наприклад, якщо сезонність є кожного року, то n = 12, 12 місяців - 1 рік, тощо
Функція def deseasonality(df,seasonality) віднімає від кожного значення у датафреймі значення, що було рік тому та повертає датафрейм[сезонність:], таким чином втрачається перший рік. Зворотньої до неї є def add_seasonality(df,diff,seasonality), яка додає сезонність з оригінального датафрейму та додає отриману сезонність до датафрейму без сезонності. Цю функцію буду використовувати для реконструкції ряду.
Після видалення сезонності часовий ряд вже є стаціонарним, скоріш за все через лінійний тренд, але для більш точного прогнозування я приберу ще й тренд.
Detrending
Тренд є середнім значенням (rolling mean) часового ряду, тому для детрендінгу потрібно відняти середнє значення від ряду, який отримала у попередньому пункті. Найпростіший спосіб зробити це алгоритм rolling mean. Я зробила дві варіації, але покажу тільки першу.
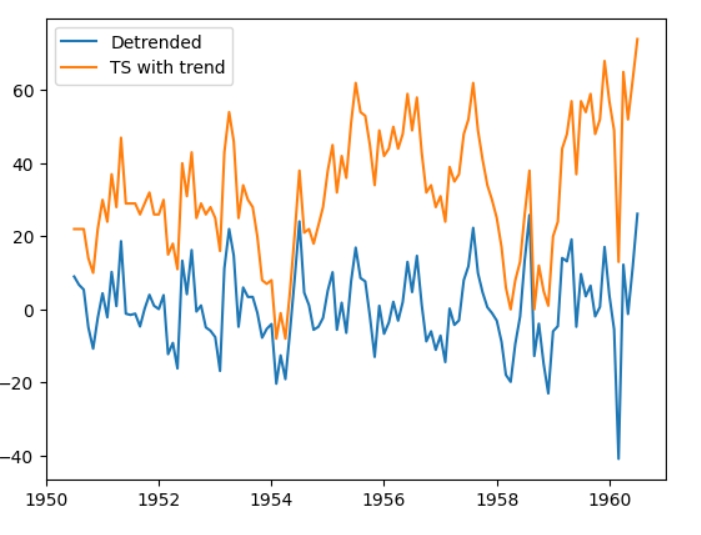
Декомпонований часовий ряд(синій) та ряд без сезонності (помаранчевий) Можна побачити, що середнє значення ряду стало близько нуля.
Функції втрати
Показниками якості моделей та прогнозування для часових рядів є функції втрати та метрики похибки. Найчастіше використовують такі функції втрати як MAE (L1 norm) - “Mean Square Error”, MSE(L2 norm) - “Mean Absolute Error”.
MAE надає кожній помилці однакову “вагу”, тобто є робастною до викидів та шуму функцією, але одночасно з цим занижує “вплив” великих помилок.
MSE в свою чергу навпаки, дає більшим помилкам більшу вагу, що робить функцію більш чутливою до викидів. Якщо модель повинна бути чутлива до помилок, обирають саме цю функцію.
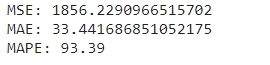
Я буду використовувати обидві функції як метрики та одну з них як функцію втрати (loss function). Що показує порівняння MAE та MSE? Для прикладу візьму наступні значення:
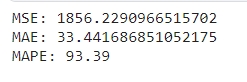
MSE у 1856 означає, що середнє значення помилки це квадрат помилки становить 1856, тобто 43.081^2 .MAE становить 33.44, тобто середнє значення помилки становить 33.44.
У цьому прикладі MSE більше за MAE у квадраті, що свідчить про наявність великих помилок, які збільшують MSE. Викиди, нелінійність або шум є причиною цьому, оскільки в цьому часовому ряді сильний шум, можна припустити, що він і є причиною. Якщо MSE менша за MAE у квадраті - модель має маленькі помилки, які і збільшують MAE . Причиною цьому є рандомність або неточність даних.
Точність часового ряду не можна знайти за стандартною функцією точності, тому для оцінки точності прогнозування та реконструкції використовую наступну метрику. MAPE є відносним значенням помилки, що можна використовувати як функцію точності за наступною формулою: 100-(MAPE*100). Функція для обчислення MAPE знаходиться у 16 комірці
Наївне прогнозування (Naive Forecasting)
Наївне прогнозування є найпростішим методом для прогнозування часового ряду, точність якого є високою тільки у разі константного (горизонтального) тренду.
Формула наївного прогнозування наступна: Yt = Yt-1: майбутнє значення часового ряду є його попереднім значенням. Так, не дуже вражаюче, але давайте все ж спробуємо. Розділяю оригінальний часовий ряд на тестову та тренувальну вибірку (останні два роки). Перше прогнозування для тестової вибірки є останнім значенням тренувальної.
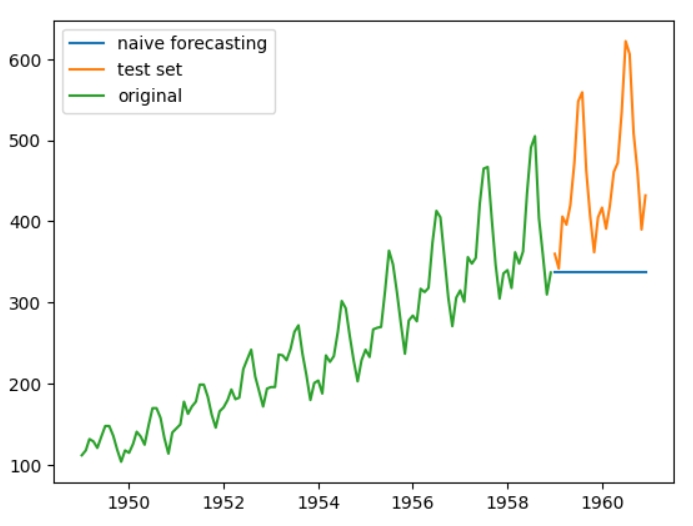
Оскільки 1 значення тестової вибірки є 317, то всі наступні значення дорівнюватимуть теж 317, в результаті чого отримуємо горизонтальну лінію. Перейдемо до більш точних методів.
Реконструкція часового ряду з rolling mean
Я не зустрічала подібного алгоритму, але він гарно ілюструє пластичність часового ряду та що з ним можна зробити. Спершу подивимося на графік часового ряду без сезонності та графік отриманого масиву rolling mean.
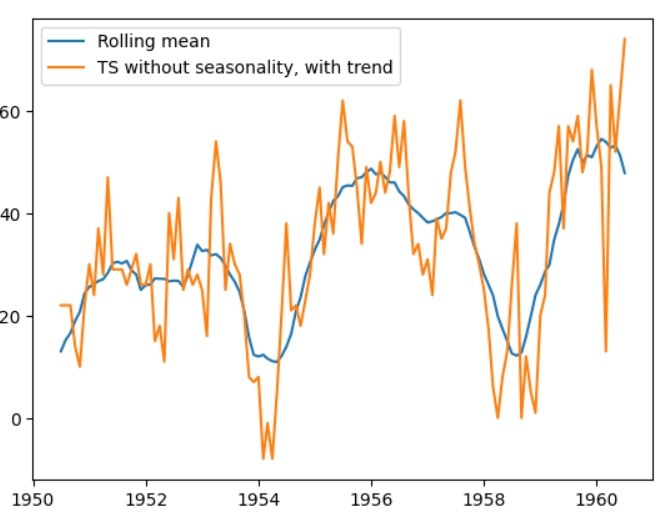
Оскільки дані не мають сезонності, самі по собі значення rolling mean є середніми значеннями, як казала вище. А що буде, якщо додати до середніх значень сезонність? Так, вийде реконструйований часовий ряд.
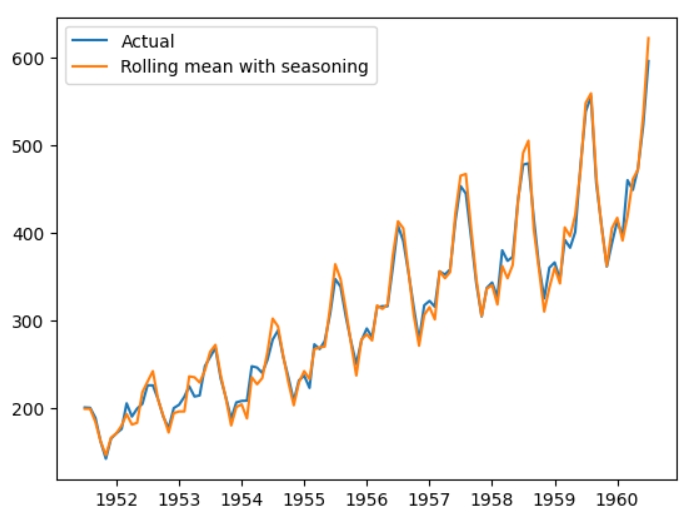
Що ж, результат доволі вражаючий, подивимося ще на точність.

Точність у 97% вражає, чому ж тоді не можна використовувати цей метод у реальних проєктах? Цей часовий ряд має має маленьку розмірність, саме через це “наївна” реконструкція спрацювала, також пригадайте, скільки всього потрібно було зробити, щоб отримати результат. Для даних з більшою розмірністю знадобилося б шукати середнє значення за всіма змінними, а операцію віднімання у багатовимірних матрицях швидко б наздогнало прокляття багатовимірності. До того ж, для обробки такого часового ряду знадобилося б набагато більше ресурсів.
У ячейках нижче можете знайти декомпозицію часового ряду за допомогою бібліотек scipy.signal та fracdiff. Ці бібліотеки не мають зворотніх функцій, тому використовувати їх не буду, але вони дуже корисні для більш складних рядів.
Декомпозиція за допомогою логарифмування
Логарифмування є популярною технікою для роботи з часовими рядами. Давайте його зробимо та подивимося на результат. Важливо використовувати np.log1p замість звичайної np.log для запобігання появі нулів.
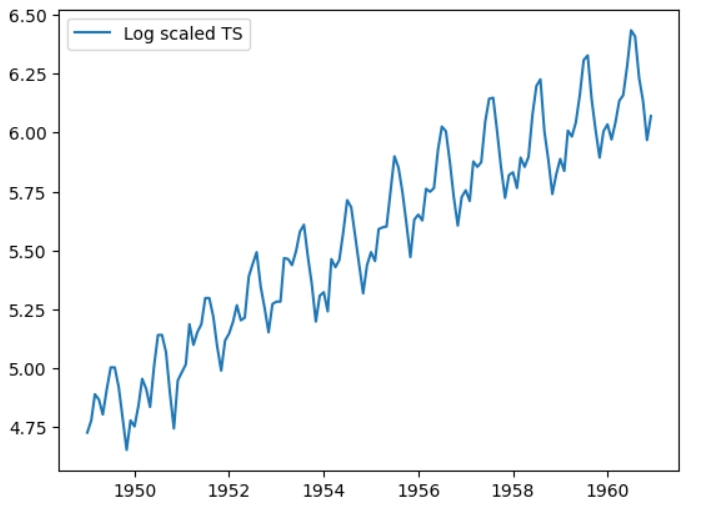
Логарифмований часовий ряд відрізняється від оригінального тільки в масштабах. Такий ряд не буде стаціонарним, оскільки в ньому залишається тренд. Використовуємо алгоритм rolling mean знову для перетворення ряду у стаціонарний.
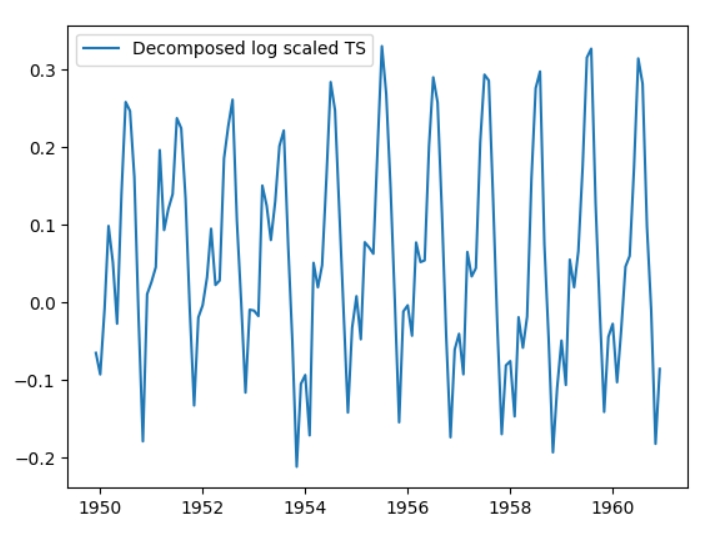
Тепер ряд є стаціонарним зі значенням р = 0.02.
Другий спосіб для перетворення логарифмованого часового ряду у стаціонарний полягає у відніманні значення у попередньому місяці від поточного. Цей спосіб є менш точним та як результат значення р = 0.07, що перевищує межу, але задля інтересу на такому часовому ряді я теж зроблю прогнозування.
Прогнозування за допомогою ARIMA
ARIMA є однією з ветеранів моделей по роботі з часовими рядами. Якість прогнозування частіше уступає перед більш потужними моделями, але знати про її існування потрібно.
Модель складається з трьох частин авторегресійної (AR), інтегрованої(I) та Ковзної середньої (MA). Кожна з цих частин має гіперпараметр, який треба знайти: p,d,q. Є два способи знаходження p,q, d частіше за все від 1 - 4:
За допомогою графіків автокореляція (acf) та часткової кореляції (pacf). На прикладі стаціонарного логарифмованого ряду без тренду datasetLogScaleMinusMovingAverage.
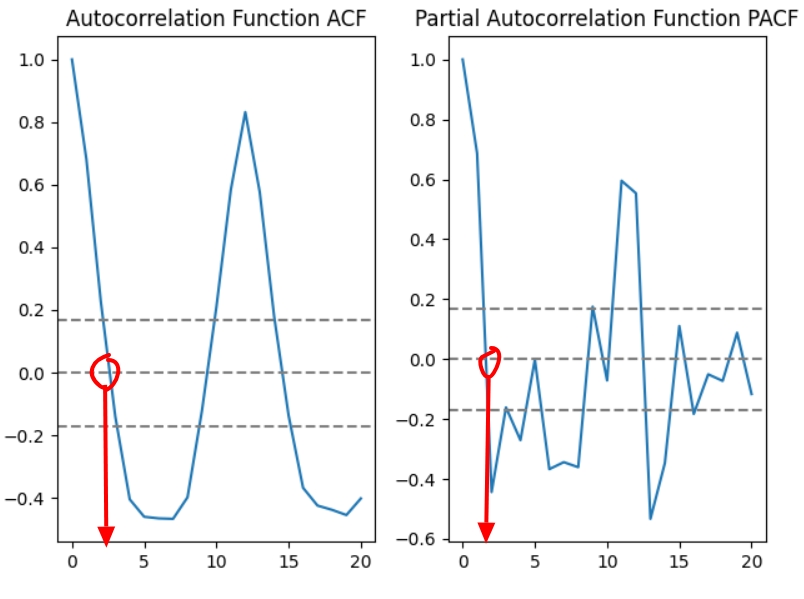
ACF PACF Щоб знайти значення р на pacf графіку треба знайти точку на осі х, у якій у=0 перший раз: р=2.
Аналогічно, q знаходять за acf графіком: q=3.
За допомогою arma_order_select_ic - функції автопідбору. Цей спосіб є більш точним, оскільки дає точні значення, на відміну від першого способу, де значення можна знайти тільки на око. Функція для знаходження параметрів є у 17 ячейці. І її результатом є:
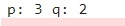
p та q, підібрані arma_order_select_ic У ARIMА я не використовувала точні значення, які знайшла, натомість вони слугували відправною точкою.
Функцією помилки для ARIMА є RSS: чим значення менше, тим якісніша модель. Для прикладу візьму попередній логарифмований ряд datasetLogScaleMinusMovingAverage, від якого відняли ковзне середнє.
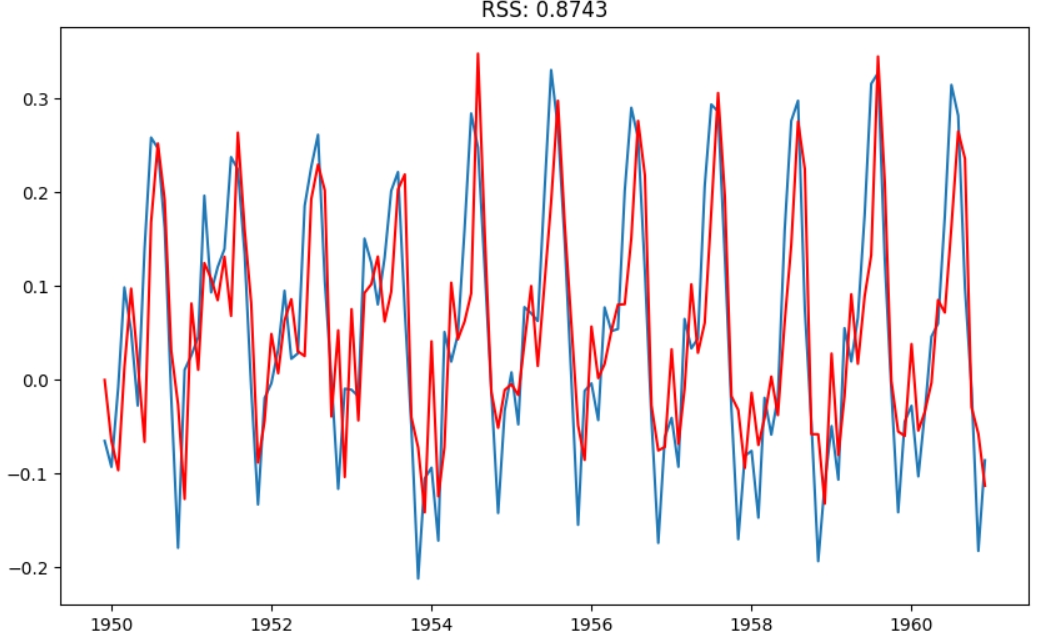
Після того, як модель навчилася на даних та дала прогнозування на основі 2х останніх років ряду, результат потрібно реконструювати у часовий ряд з сезонністю та трендом. datasetLogScaleMinusMovingAverage - це логарифмований часовий ряд, від якого відняли ковзне середнє. Найпростіший спосіб реконструкції - це додати ковзне середнє логарифмованого ряду та експонентувати результат, щоб отримати реконструйований часовий ряд.
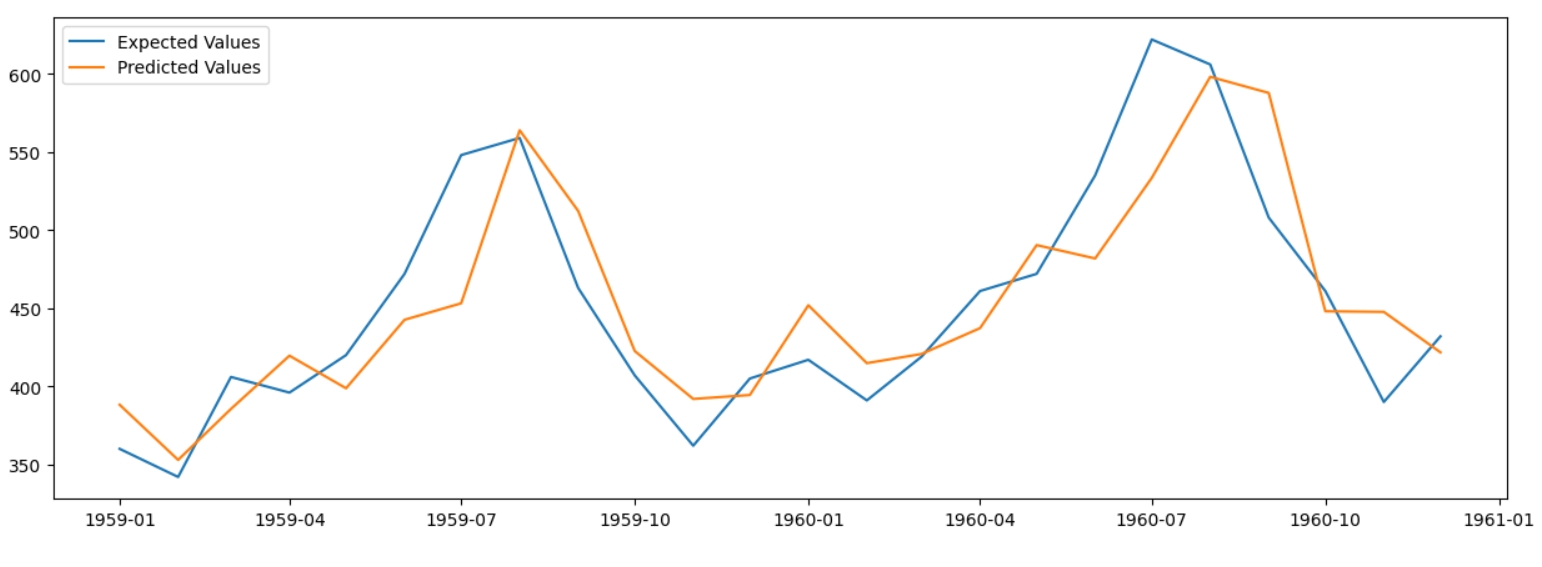
Точність: 93.25%, що доволі непогано.
Такий спосіб реконструкції підходить для більш глибшого розуміння роботи з часовими рядами, аніж для використання для реальних проєктів.
SSA (Singular -Spectrum Analysis)

Це звучить цікаво, аніж страшно, повірте.
SSA - це один з тих методів, про які чомусь ніхто не говорить, попри їх високу ефективність. Суть метода проста - зробити всі ті ж самі кроки, що я зробила до цього, але набагато швидше та з застосуванням більш складної математики. Його можна розділити на 3 частини: декомпозиція часового ряду, реконструкція та прогнозування. Метод доволі простий для розуміння, але використовує доволі складні методи, як SVD, тому залишу теорію для вашого власного розгляду. Коротко: перетворення часового ряду на багатовимірну матрицю Генкеля, далі, за допомогою SVD розділити отриману матрицю на сигнали, з отриманих сигналів обрати найбільш “впливові” та реконстроювати матрицю з їх допомогою, на основі реконструйованої матриці передбачити майбутні значення.
SSA реалізован у репозиторії PySSA, який і буду використовувати.
Після того, як матриця, отримана з часового ряду, декомпозована через ssa.decompose(verbose=True) на сигнали, подивимося ближче на них.
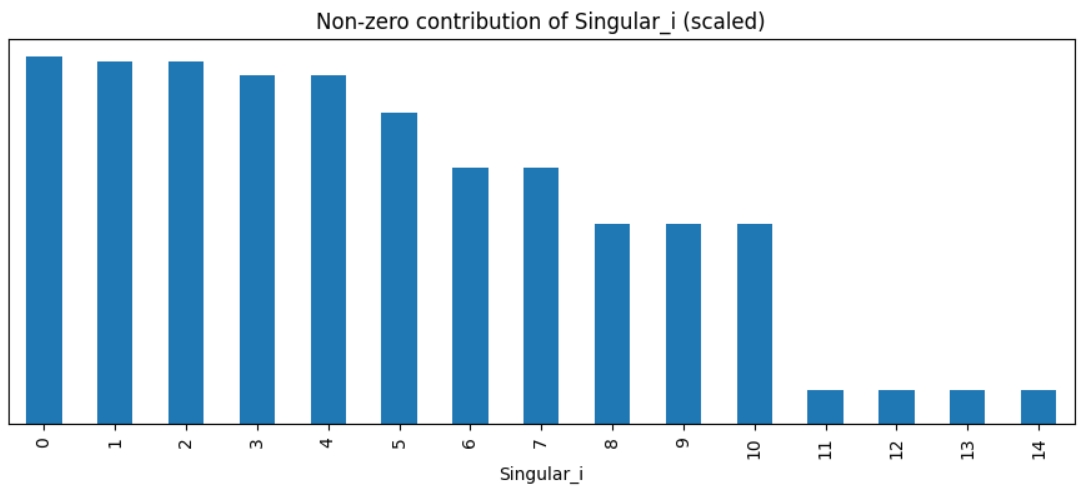
Перші 5 сигналів найбільше впливають на ряд, їх для початку і візьму для реконструкції та прогнозування.
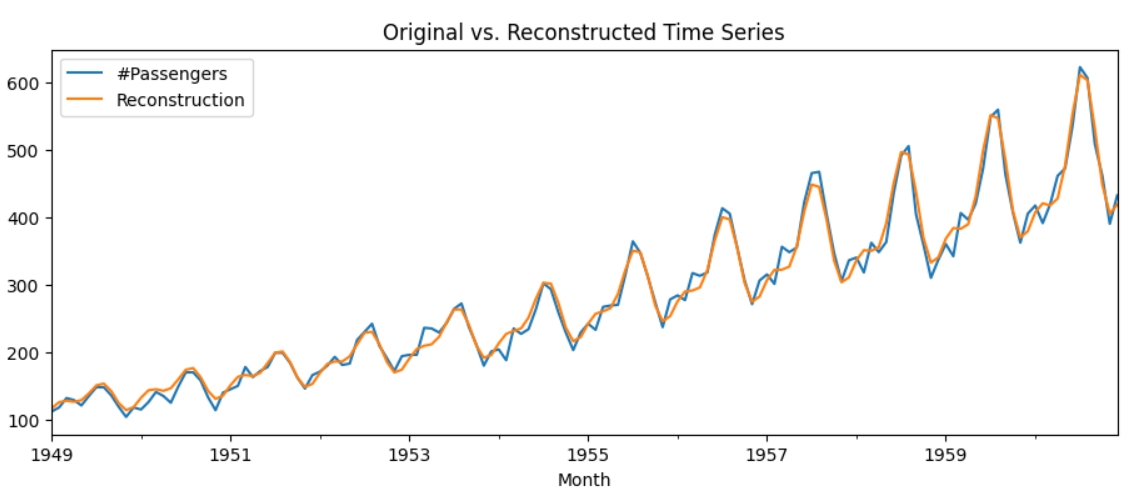
Реконструкція доволі точна, подивимося, як SSA передбачить значення. Для цього використаю ssa.forecast_recurrent з return_df=True, щоб повернути датафрейм та розрахувати точність прогнозування.
ssa_forecast_5=ssa.forecast_recurrent(steps_ahead=48, singular_values=streams5, plot=True,return_df=True)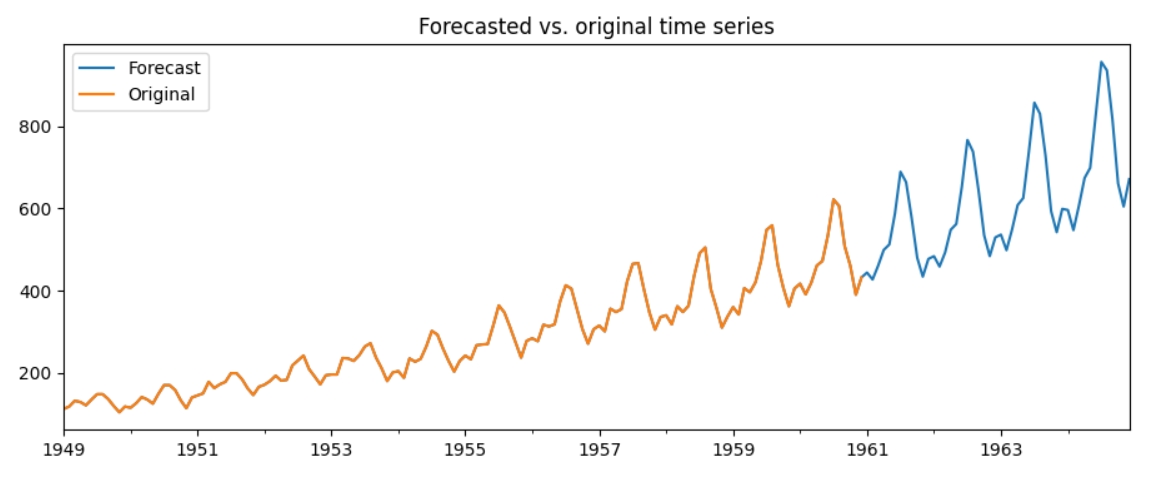
Спочатку можна подумати, що прогнозування позначене тільки синім кольором та починається з 1961 року, але насправді прогнозування починається з 1949 року, тобто графіки оригінального часового ряду та передбачуваного абсолютно збігаються. Точність дорівнює вражаючим 100%.
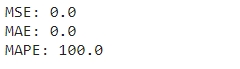
Якщо реконструювати та передбачити ряд на основі 10 сигналів, замість 5, точність не зміниться. Подивимося прогнозування на 10 років вперед.
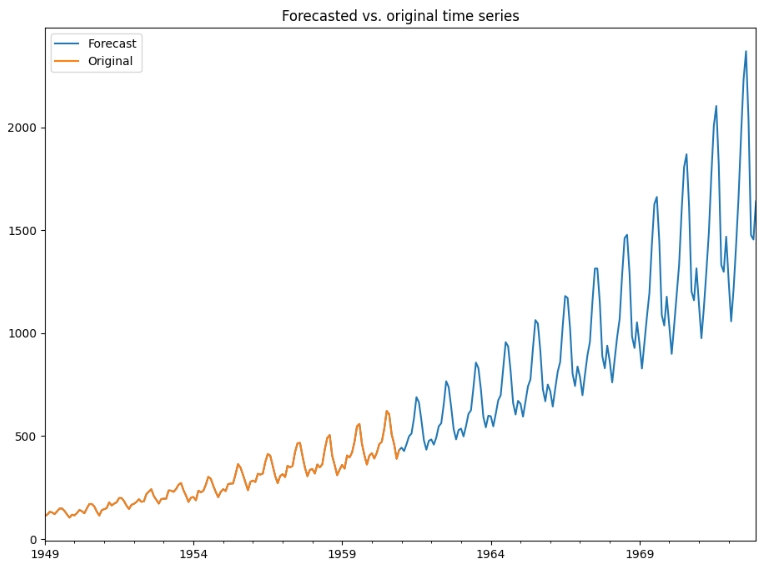
Як передбачала у попередній частині, дисперсія буде збільшуватися. Це прогнозування навіть частково відповідає дійсності, бо у 70х роках почався “бум” на авіаперельоти.
Eкспоненціального згладжування (Exponential Smoothing)
Експоненціальне згладжування — це метод прогнозування часових рядів для одновимірних даних.
Прогнози, створені за допомогою методів експоненціального згладжування, є середньозваженими значеннями минулих спостережень, причому ваги зменшуються експоненціально, чим далі спостереження від початкової дати. Іншими словами, чим пізніше спостереження, тим вища відповідна вага.
Експонціальне згладжування схоже на ARIMA, але окрім зваженої суми минулих спостережень ще використовують експоненціально зменшувану вагу минулих спостережень.
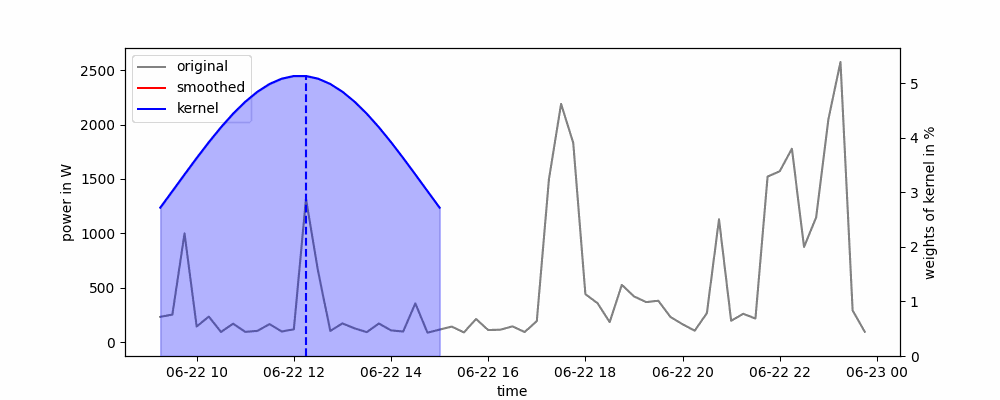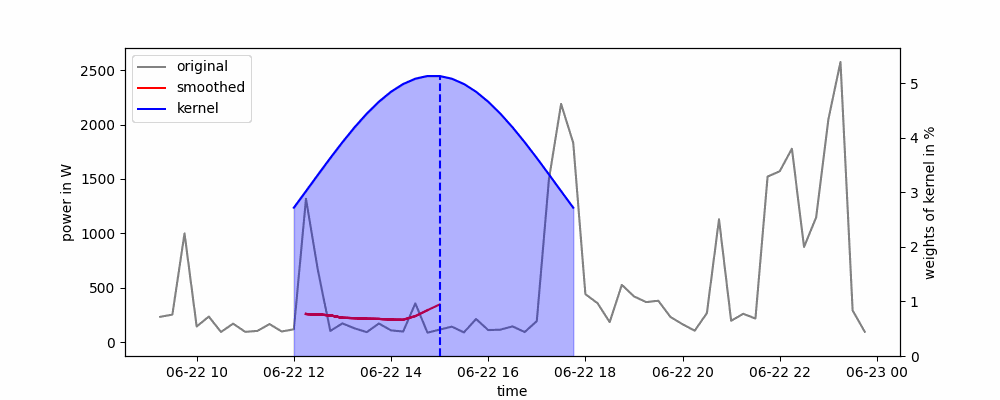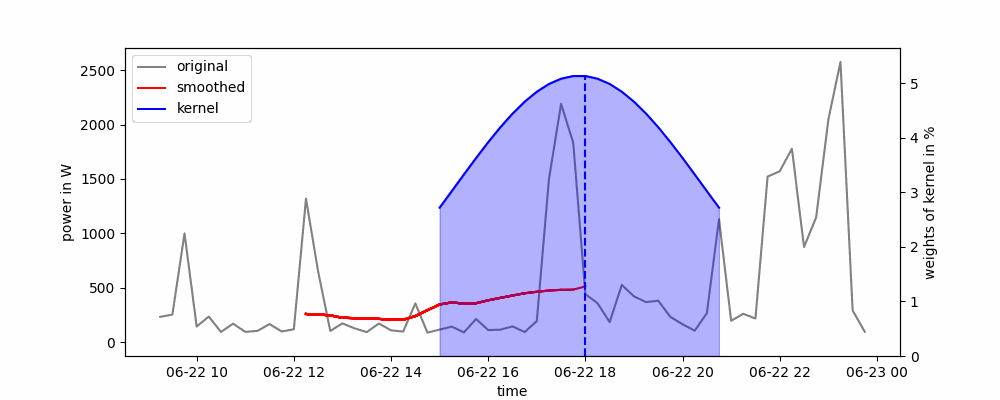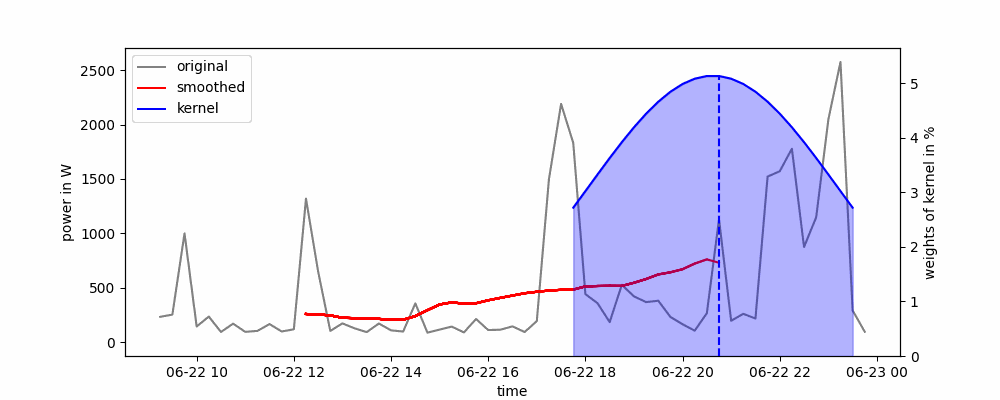
Я буду використовувати вже реалізовану модель з statsmodels.tsa.holtwinters. Існують три вида моделі експоненціального згладжування: проста, подвійна та потрійна. Проста модель може працювати тільки зі стаціонарним часовим рядом, подвійна працює з рядом з трендом, але без сезонності, третя працює з повністю нестаціонарним рядом. Саме останню модель я і буду використовувати.
from statsmodels.tsa.holtwinters import ExponentialSmoothing
# prepare data
data = pd.read_csv('/kaggle/input/air-passengers/AirPassengers.csv')
data['Month'] = pd.to_datetime(data['Month'])
split=120
train_exp=data[:split]
val_exp=data[split:]
# create class
model_exp_sm = ExponentialSmoothing(train_exp['#Passengers'], seasonal_periods=12,
trend="add",
seasonal="add",
initialization_method="estimated").fit()
# make prediction for 4 years: 2 years for val set and another 2 years for forecasting
y = pd.DataFrame(model_exp_sm.forecast(48), columns=["pred"])Спершу, розділяю датасет на тренувальний та валідаційний. Зверніть увагу, у data індексами є числа, а не дати, на відміну від датафрейму, який використовую для всіх інших моделей. Далі, створюю клас, тренд є лінійним, а сезонність точно повторюється кожного року, тому їм надаю значення "add", якщо тренд є експонентою буде "mul". Для прогнозування та тестування на валідаційному наборі створюю спільний датаферйм: перші два роки для тестування, інші два роки для прогнозування майбутніх значень.
Параметри моделі можна подивитися наступним способом:
model_exp_sm.model.params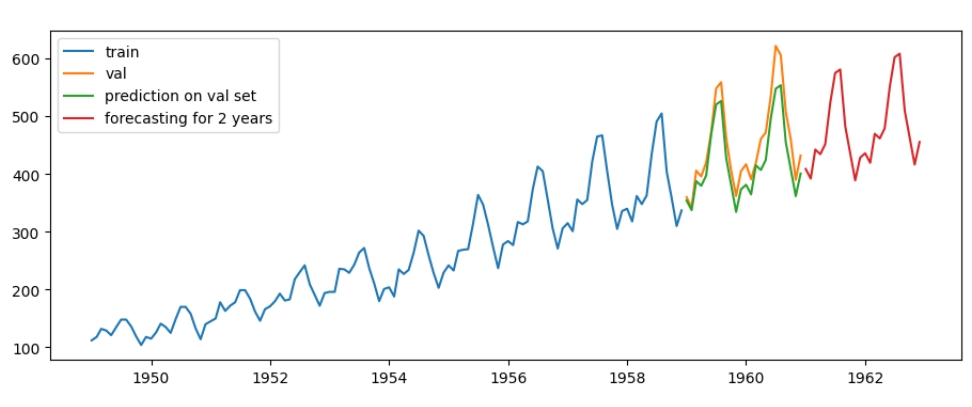
Точність на валідаційному наборі становить 93.36%

прогнозування через FFT
Перетворення Фур’є - це перетворення комплексної змінної в іншу за конкретними параметрами. Такі перетворення частіше за все використовують для роботи з сигналами, але їх також можна використовувати для декомпозиції та прогнозування часового ряду. Для роботи з часовими рядами використовують дискретні перетворення Фур’є, оскільки значення часового ряду вимірюються у конкретному інтервалі.
Перетворення Фур’є включає в себе багато методів математичного аналізу, тому якщо вам цікаво дізнатися більше, пропоную переглянути цю статтю.
Numpy має оптимізовану реалізацію дискретних перетворень Фур’є - FFT (Fast Fourier Transform). Я знайшла вже готову реалізацію та отримала наступний результат:
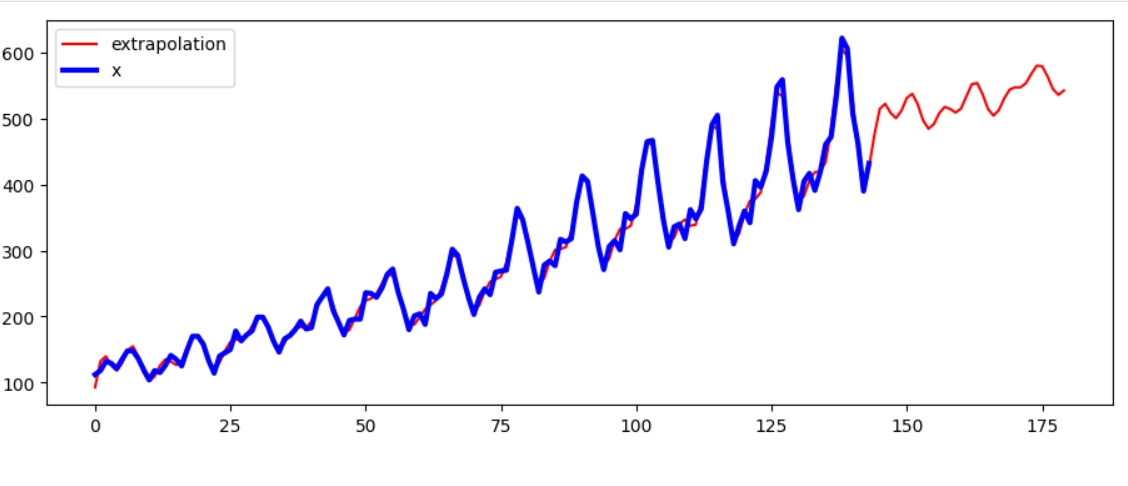

Прогнозування для вже існуючого ряду доволі точні, проте прогнозування майбутніх значень не має потрібної сезонності.
GRU
Для всіх наступних моделей я буду використовувати оригінальний нестаціонарний датасет. Традиційно вважається, що LSTM є більш точною за GRU моделлю, але для цього часового ряду найкращі результати показала саме GRU. У цьому розділі я розповім про підготовку даних, тюнінг моделі та прогнозування майбутніх значень.
Підготовка часового ряда. До нейромережі подається два вида даних: змінні (х) та цільове значення (у), оскільки оригінальний часовий ряд має тільки одну змінну, кількість пасажирів, його потрібно перетворити у датафрейм, який можна розділити на х та у. Для цього я утворю матрицю з оригінальною змінною та лагами на 3 місяці:
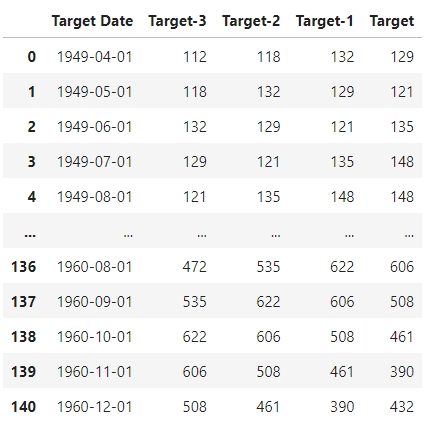
Утворена матриця Target -3: значення змінної 3 місяці тому, Target -2: два місяці тому та Target -1: місяць тому. Таким чином, утворилася матриця, де перші 4 стовбці - х, а останній стовпець - у. Через такі махінації часовий ряд втратив перші три місяці.
Нормалізація. Для прискорення навчання та більш якісних результатів отриману матрицю потрібно нормалізувати. MinMaxScaler() - це єдиний варіант нормалізатора, оскільки розподіл часового ряду не є нормальним. Важливою тонкістю при нормалізації є порядок її проведення: метод fit_transfom викликається на тренувальному наборі, transform викликається на тестувальному та валідаційному. Спочатку розділю матрицю на трейн, тест та валідаційний набори. Функція def scaling(df,train) нормалізує окремо кожний сет, bool змінна train визначає чи є сет тренувальним (train=True), чи ні. Цікавою особливістю є те, що якщо розділити дані по повних циклах сезонності, тобто по роках, точність підвищиться.
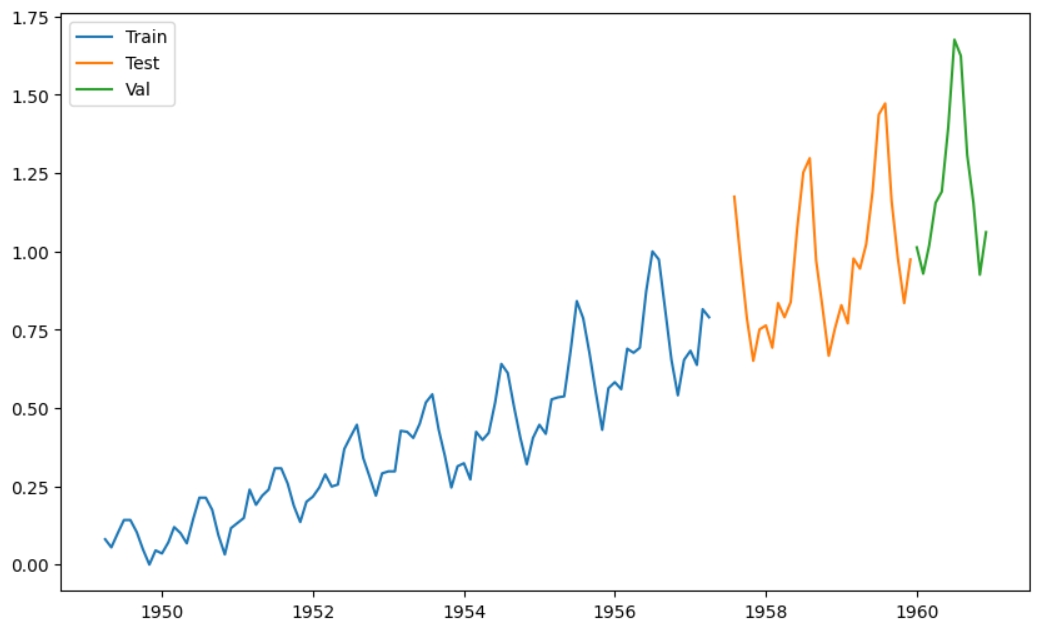
Такий спосіб розділення на train/test/val дає меншу точність 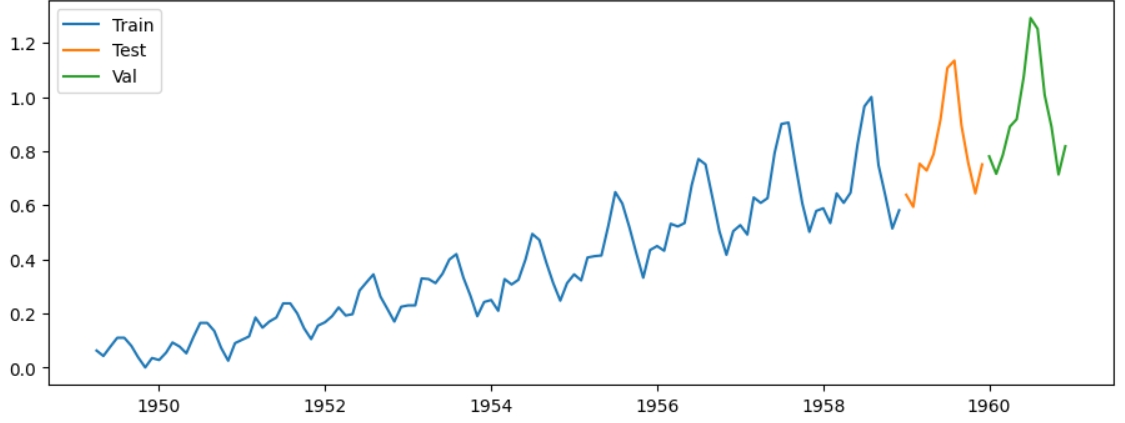
А такий більшу
Тюнінг
Тюнінг - це спосіб максимально швидко знайти модель з найвищою точністю. Як і у більшості методів машинного навчання, тут теж є важлива деталь: гарну модель можна отримати лише в разі правильно підібраних гіперпараметрів та їх ранжування. Як тюнер я використовую keras-tuner та клас MyHyperModel(HyperModel) для створення моделі. Шукати гіперпараметри можна і за допомогою більш старих оптимізаторів, таких як Random Search, але краще використовувати Hyperband, який більш швидкий та якісний. Найкращу модель зберігаю.
best_hps = tuner.get_best_hyperparameters(num_trials=1)[0]Навчання
Далі, отриману модель слід навчити на підготовлених даних. Щоб уникнути перенавчання я використала EarlyStopping() та ModelCheckpoint(), щоб зберігти найкращі ваги. Робити це через restore_best_weight = True EarlyStopping() не завжди гарна ідея через те, що ваги будуть зберігатися лише в тому разі, якщо EarlyStopping() зупинився через обмеження, задане у patience, а не коли дійшов до останньої епохи, що буває доволі часто.
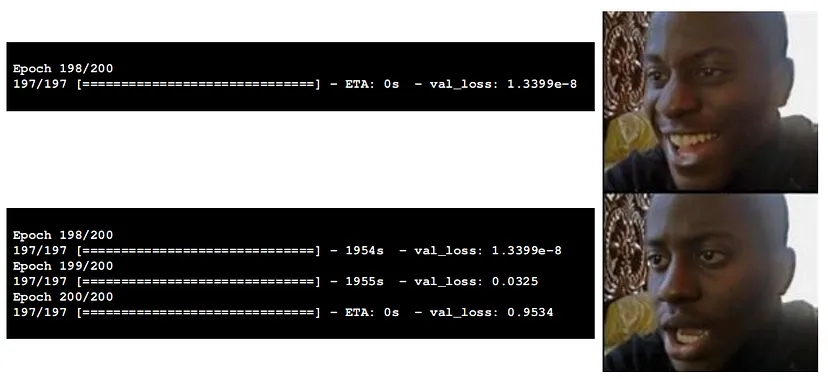
Після успішного навчання завантажую найкращі ваги до моделі
#load best weights to the model
model.load_weights("/kaggle/working/checkpoint.model.h5")На функції втрат можна побачити невелике перенавчання

Для перевірки точності моделі на валідаційних даних, потрібно передбачити значення через model.predict() та зробити дані знову не нормалізованими через scaler.inverse_transform(). Точність моделі складає 90%, що не дуже вражає для такої потужної моделі та таких легких даних.
Прогнозування майбутніх значень
Спочатку створюю масив, що місить кожен місяць з 1961 по 1962 рік.
first_year=pd.date_range("1961-01-01","1961-12-01", freq='MS')Далі, потрібно створити 3 місячні лаги. Оскільки валідаційний сет на рік менший за дати, для яких буду передбачати значення, то можна взяти лаги з валідаційного сету:
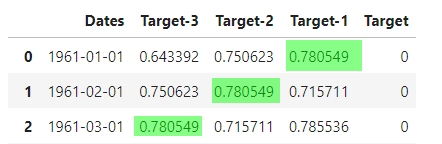
Далі, аналогічно до валідаційного сету, передбачаються значення через model.predict() та повертаються до ненормалізованого стану.
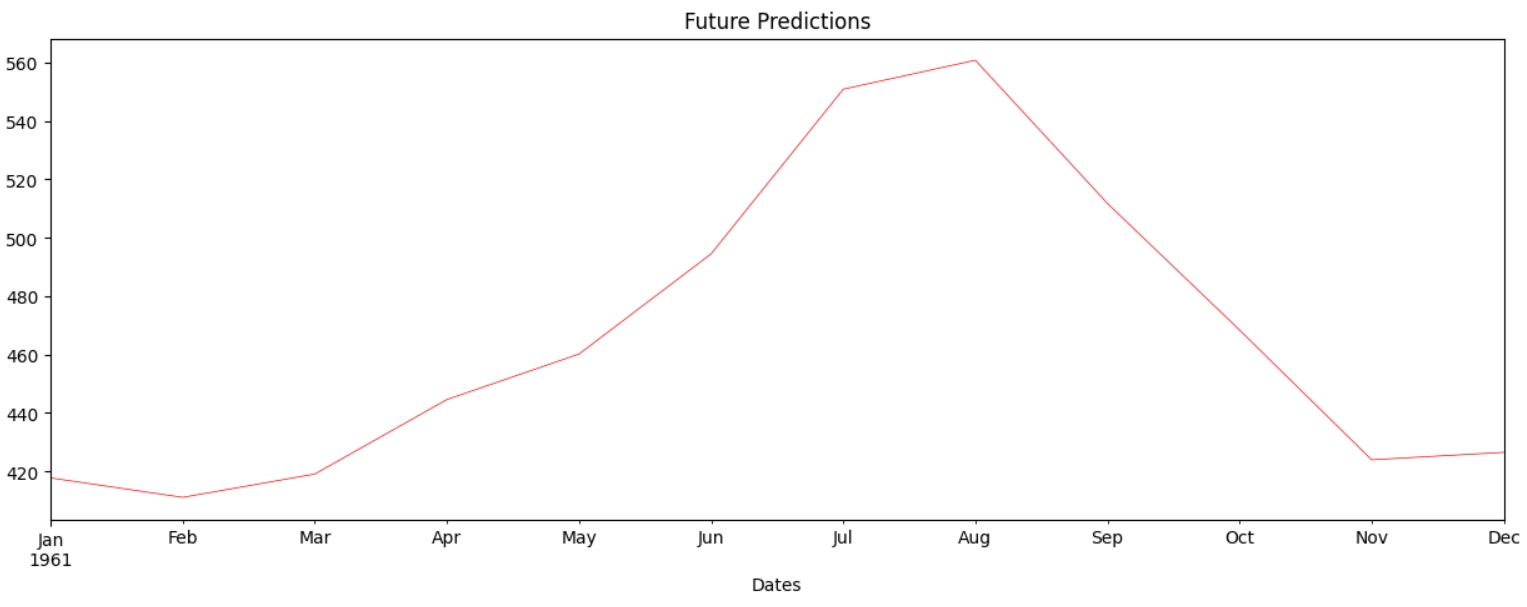
XGBoost Regressor
Це ще одна модель, яку можна часто зустріти у задачах прогнозування часового ряду. Підготовка даних для цієї моделі ще простіша, оскільки її основа - це Random Forest, для якого не потрібно нормалізовувати дані. Все, що потрібно зробити з даними - це створити матрицю, схожу на ту, що використовувала для GRU.
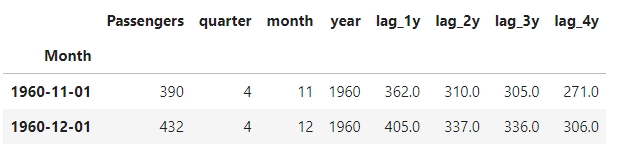
Додала додатковий четвертий лаг та розділила дату на місяць, квартал та рік.
Тюнінг
Для тюнінгу використовую HyperOpt, особливість цього тюнера в тому, що він зберігає всі результати навчання, в тому числі найкращу модель у Trials(). Зберігаю найкращу модель та підготую дані для навчання.
def getBestModelfromTrials(trials):
valid_trial_list = [trial for trial in trials
if STATUS_OK == trial['result']['status']]
losses = [ float(trial['result']['loss']) for trial in valid_trial_list]
index_having_minumum_loss = np.argmin(losses)
best_trial_obj = valid_trial_list[index_having_minumum_loss]
return best_trial_obj['result']['Trained_Model']Підготовка даних для навчання
Перед розділенням даних на тестовий та тренувальний набір, я створила валідаційний набір з df_w_lags, оскільки кросс - валідація створює тільки тестовий та тренувальний набір. Разом з XGBoost часто використовують кросс- валідацію, яка розділяє дані на тестові та тренувальні наступним чином.
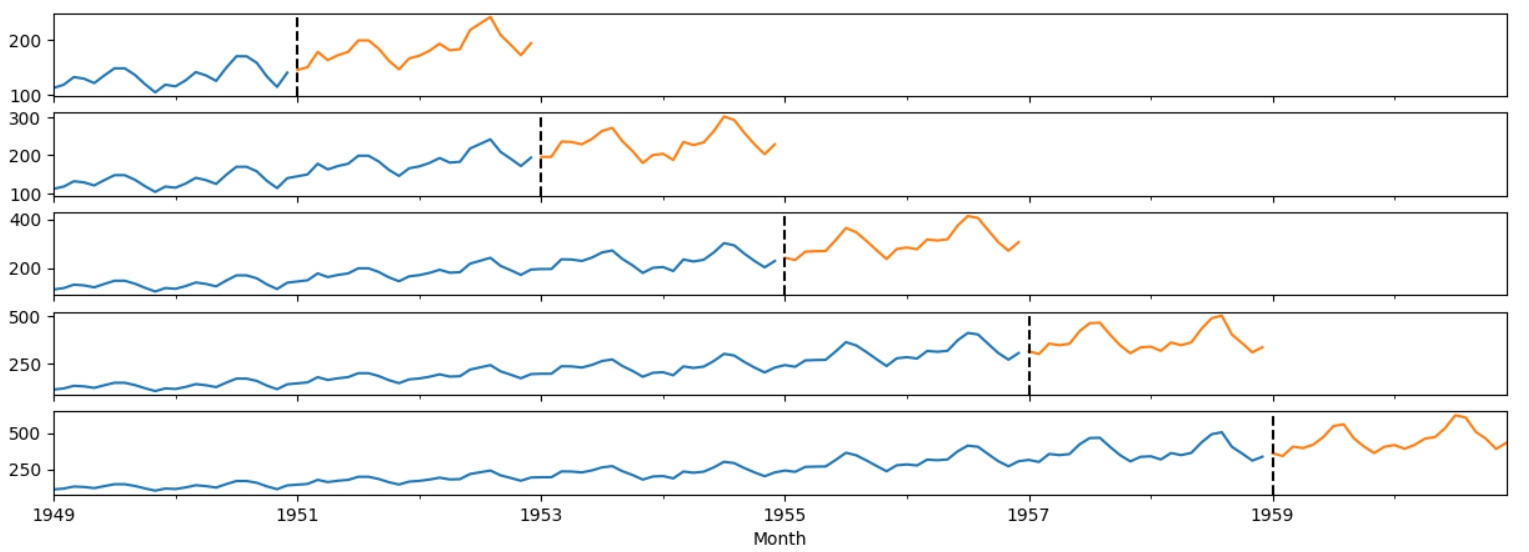
Синім позначені тестові дані, помаранчевим - тествувальні. Такий алгоритм дає змогу більш якісно обробити дані, оскільки тренувальні та тестові сети змінюються.
Чому ж тоді не використовувати дані, розділені крос - валідацією, для тюнінгу? Швидкість тюніга напряму залежить від кількості даних та розміру пошукового поля, тобто крос - валідація тільки уповільнила б тюнінг.
Навчання
Функція cross_val_fit повертає якість моделі для кожного валідаційного спліта та саму модель. Як функцію втрати обрала MAE, щоб зменшити значення великих помилок.
xgb_reg,scores=cross_val_fit(xgb_reg_tun,df_w_lags)
По графіку можна побачити, що модель трішки перенавчена, навчання можна було зупинити після 90 епохи. Також можна подивитися, яка змінна найбільше вплинула на модель:
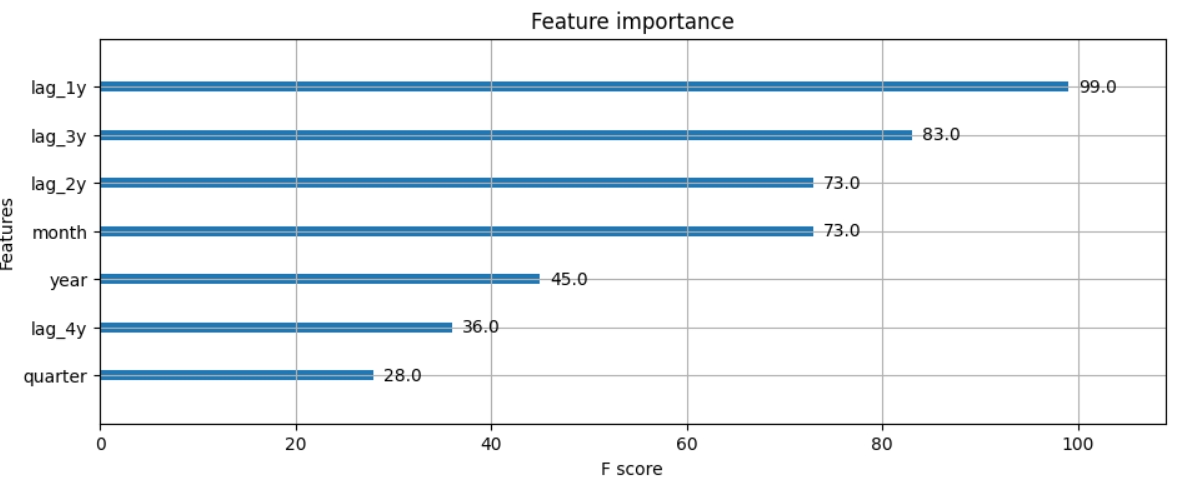
В моєму випадку це лаги 1 місяця.
Прогнозування майбутніх значень
Аналогічно до прогнозування майбутніх значень для GRU, створюю матрицю з лагів попередніх років для прогнозування за допомогою конкатенації. Стовпчик pred містить прогноз.

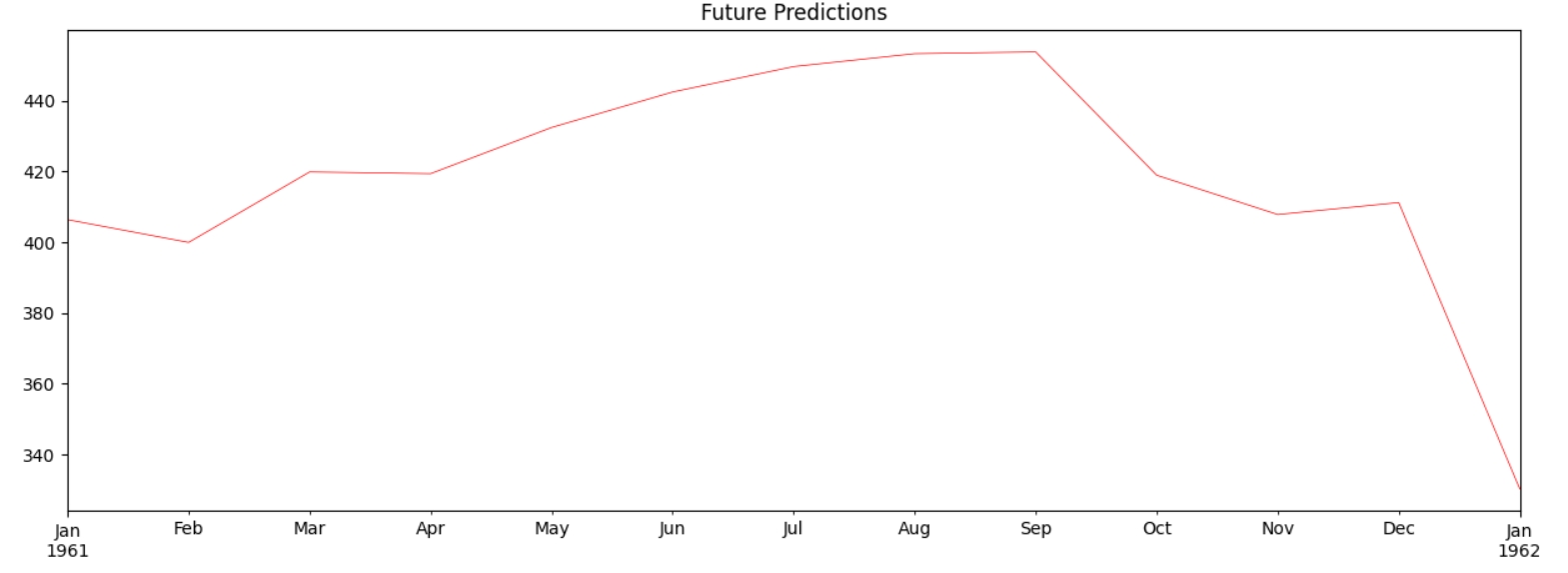
XGBoost теж вловлює загальну сезонність, але пікове значення досягається у вересні, а не у серпні.
Prophet
Остання та найлегша у створенні модель. Prophet створила команда вчених з Facebook, основна особливість полягає в тому, що Prophet декомпозує модель під час навчання, на відміну від інших моделей.
Для навчання дані повинні надходити тільки в наступному вигляді:
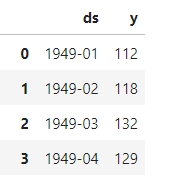
І так, це вся підготовка, яка потрібна для цієї моделі. Далі, отриманий датафрейм розділяю на тренувальний та валідаційний (останній рік).

Пікового значення ряд набуває на 7 місяць, липень, замість серпня.
Точність є найбільшою серед усіх моделей:
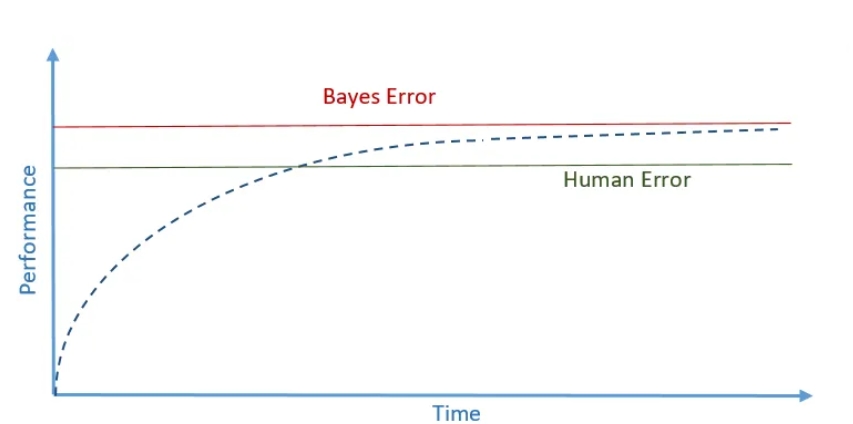
Human Error vs Bayes (Perfect ) Error
Метрики точності та помилки -- це прекрасний спосіб зрозуміти, справжню якість моделі, але що робити, якщо після оптимізації якість підвищилась трішки і все ще менше бажаних 100%?
Чи повинна ідеальна модель мати 100% точності? У Машинному навчанні є два типи помилок, щоб зрозуміти це. Перша помилка - “Human Error“ - людська помилка. Вона репрезентує точність людських висновків на тих же даних, на яких навчається модель. Звичайно, ніхто не буде набирати фокус - групу, щоб знайти показник цієї оцінки, але це і не треба, оцінку можна передбачити приблизно. Я не змогла знайти точний відсоток, на який можуть помилитися фінансисти та математики при передбаченні часового ряду, але припустимо, що помилка становить 8%. Для знаходження роблять наступну табличку (ці значення я також припустила). Уявіть 3 - 4 групи людей з різними знаннями у сфері, до якої належать дані. Відповідно до use case (як модель буде використовуватися), найнижча помилка може бути “ідеальною“ помилкою, людська помилка - середня помилка або середнє між середньої помилкою та найбільшою. Якщо висока точність моделі є критичним показником, наприклад модель розпізнає ракові пухлини, то тоді “ідеальна“ помилка повинна бути вище за найменшу помилку з таблиці, людська помилка - вище за середню помилку з таблиці.
Професія людини | Відсоток помилки |
|---|---|
- Людина без досвіду передбачення часового ряду (базове знання математики) - Математик/фінансист - Математик/фінансист з практичним досвідом | 30% 8% 3% |
Функція втрати моделі, після переходу через значення людської помилки, “потрапляє“ на плато, де не може знайти мінімум, відповідно якість моделі залишається сталою. Модель вважається хорошою, якщо її точність вище людської помилки.
Другий тип помилок - “Bayes Error“ або “ідеальна/недосяжна помилка“. Це помилка, яку в теорії може досягти модель при ідеальному розподілі даних, налаштуванні гіперпараметрів, тощо. Функція втрати моделі завжди буде нижче та ніколи не перейде межу ідеальної помилки.
Інтуїтивно це можна пояснити наступним чином: людина може передбачити, якою стороною впаде монетка (теорія вірогідності), але якщо крутяться сотні монеток, передбачити стає набагато складніше.
Порівняння точності всіх методів
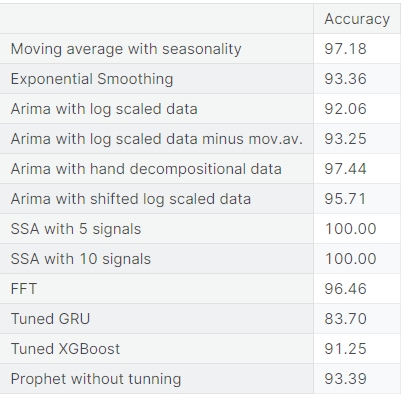
Функції втрат майже всіх моделей знаходяться між горизонтальними осями людської та ідеальної помилки.
Можна сказати, що найвищу точність має SSA, але ця точність для маленьких даних з однією змінною. Останні три моделі показують найвищу якість для більш складних даних.
Післямова
Дякую, що дочитали, сподіваюся було корисно та цікаво! Як можете побачити, я використовую англомовну літературу, але розумію, що не всім такий спосіб вивчення є зручним, тому прошу поділитися у коментарях україномовними каналами, статтями, аккаунтами в Твіттері, тощо. З ваших відповідей я складу список та опублікую. Дякую!
Використані джерела
https://medium.com/@doleron/never-use-restore-best-weights-true-with-earlystopping-754ba5f9b0c6
https://towardsdatascience.com/fourier-transform-for-time-series-292eb887b101
https://www.kdnuggets.com/2023/08/leveraging-xgboost-timeseries-forecasting.html
https://medium.datadriveninvestor.com/mastering-advanced-time-series-techniques-7b1080cef853
https://www.databricks.com/blog/2021/04/15/how-not-to-tune-your-model-with-hyperopt.html
https://www.linkedin.com/advice/0/what-difference-between-mean-squared-error-tz1mc
https://medium.com/@rithpansanga/optimizing-xgboost-a-guide-to-hyperparameter-tuning-77b6e48e289d
https://hyperopt.github.io/hyperopt/getting-started/search_spaces/
https://www.machinelearningplus.com/time-series/augmented-dickey-fuller-test/
https://towardsdatascience.com/stationarity-in-time-series-a-comprehensive-guide-8beabe20d68
https://towardsdatascience.com/seasonality-of-time-series-5b45b4809acd
https://towardsdatascience.com/the-fourier-transform-1-ca31adbfb9ef
https://towardsdatascience.com/fourier-transform-for-time-series-292eb887b101
https://medium.com/@doleron/never-use-restore-best-weights-true-with-earlystopping-754ba5f9b0c6

