Пишу про ряд Фур’є, важливий елемент теорії сигналів та обробки інформації.
Вступ

Жан Батист Жозеф Фур'є був розумним дядьком, якого настільки турбували металеві пластини (Фур’є ввів цей ряд з метою розв’язування рівняння теплоти в металевій пластині), що він дав нам цілу науку, аналіз Фур’є, яка сильно допомогла розвитку комунікацій.
Ряд Фур'є - це математичний інструмент, який використовується для розкладання складних функцій на прості синусоїдальні (синуси та косинуси) складові. Цей розклад дозволяє виразити будь-яку періодичну функцію у вигляді суми гармонічних компонентів з різними амплітудами і частотами. Розкладання функції у вигляді ряду Фур'є допомагає розглядати її структуру та властивості на різних частотних складових.
Зазвичай ряд Фур'є використовується у наступних контекстах:
Обробка сигналів: Ряд Фур'є допомагає аналізувати сигнали у частотному домені, що може бути корисним у спектральному аналізі сигналів, включаючи аудіо, відео та зображення.
Математична аналіз: Ряд Фур'є використовується для розв'язання диференціальних рівнянь, а також для дослідження властивостей функцій у зв'язку з їхніми частотними компонентами.
Теорія сигналів і комунікацій: Ряд Фур'є є важливим інструментом для аналізу та моделювання сигналів у системах зв'язку та обробки інформації.
Геометрична оптика: У фізиці ряд Фур'є використовується для аналізу та моделювання розповсюдження світла та інших хвильових явищ.
Для того, щоб розкласти функцію у ряд Фур’є, функція повинна задовільняти наступні умови:
Періодичність: Функція, яку ви плануєте розкласти у ряд Фур'є, повинна бути періодичною. Це означає, що існує певний період T, такий що f(t) = f(t + T) для всіх значень t.
Визначений інтервал: Обмеження області, на якій ви аналізуєте функцію, важливе для обчислення ряду Фур'є. Зазвичай вибирається певний відрізок, який включає один повний період функції.
Абсолютно інтегровна функція: Функція повинна бути абсолютно інтегровною на вибраному інтервалі, що означає, що інтеграл від модуля функції повинен бути скінченним. (Функція Дірака, наприклад, має нескінченну амплітуду, що не дозволяє її інтегрувати)
Обчислення ряду Фур’є це лише розрахунки коефіцієнтів Фур’є.
Якщо функція парна, то Bn = 0, а якщо непарна, то An = 0. Тобто для парної функції не обчислюється частина з синусом, а для непарної не обчислюється частина з косинусом.

Розкладаємо функцію в ряд Фур’є:
Ми розкладемо оригінальну функцію (представлена, як вектор на інтервал [a, b]) на групу гармонік
import numpy as np
import matplotlib.pyplot as plt
# Параметри
a = -np.pi
b = np.pi
num_terms = 6 # Кількість членів ряду
num_points = 400 # Кількість точок
# Вектор x для точок на інтервалі [a, b], результат оригінальної функції
x = np.linspace(a, b, num_points)
# Побудова графіка на основі ряду Фур'є
plt.figure(figsize=(10, 6))
colors = ['b', 'g', 'r', 'c', 'm', 'y', 'k']
original_function = np.zeros_like(x)
for n in range(1, num_terms + 1): # Починаємо з одиниці, щоб уникнути нульової гармоніки
# Розраховуємо тільки для косинуса
coefficient = 2 / (b - a) * np.trapz(np.cos(n * x), x)
harmonic = coefficient * np.cos(n * x)
original_function += harmonic
plt.plot(x, harmonic, label=f'Гармоніка {n}', color=colors[(n - 1) % len(colors)])
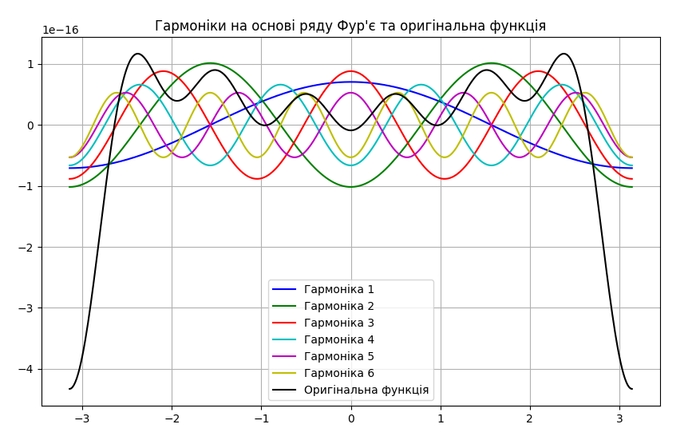
plt.plot(x, original_function, label='Оригінальна функція', color='black')
plt.legend()
plt.title('Гармоніки на основі ряду Фур\'є та оригінальна функція')
plt.grid(True)
plt.show()
Для неперіодичних функцій замість ряду Фур'є використовується перетворення Фур'є.
