Скалярний, векторний та мішаний добутки у Python

Всіх вітаю! Предметом обговорення у сьогоднішній статті будуть скалярний, векторний та мішаний добутки у Python за допомогою бібліотеки numpy. У цій статті ми розглянемо як реалізувати усі ці добуки через відповідний функціонал та дещо дізнаємося про їх суть.

Встановлення numpy

Windows:

pip install numpy

MacOS:

pip3 install numpy

Linux:

pip install numpy

Скалярний добуток

За скалярним добутком у результаті обчислення ми одержуємо число, або скаляр іншими словами.

Формула скалярного добутку виглядає так:

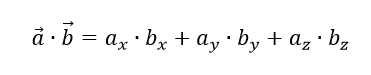
Приклад на основі двовимірних векторів

Першим кроком імпортуємо бібліотеку numpy:

import numpy as np

Створюємо два вектори:

vector_a = np.array([2, 4])
vector_b = np.array([9, 6])

Для знаходження скалярного добутку між двома векторами використовуємо функцію dot():

scalar_product = np.dot(vector_a, vector_b)
print(f"Скалярний добуток: {scalar_product}")

Результат:

Скалярний добуток: 42

Приклад на основі тривимірних векторів

Визначаємо вектори:

vector_a = np.array([-1, 14, 3])
vector_b = np.array([0, -4, 7])

Знаходимо скалярний добуток для нових векторів:

scalar_product = np.dot(vector_a, vector_b)
print(f"Скалярний добуток: {scalar_product}")

Скалярний добуток: -35

Векторний добуток

За векторним добутком ми у результаті отримуємо не число, як у скалярному добутку, а вектор.

Формула векторного добутку виглядає так:

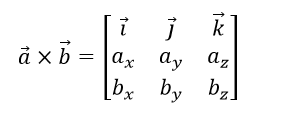
Де i, j, k — це орти або так звані одиничні вектори, котрі відповідно вказують напрямки осей x, y, z у декартовій системі координат. У цій же системі координат дані орти приймають такі значення: i = (1, 0, 0), j = (0, 1, 0), k = (0, 0, 1).

Тривимірні вектори — єдині можливі параметри

З векторним добутком все цікавіше. Так як векторний добуток можливий тільки для тривимірних векторів, то ми визначаємо тільки їх:

vector_a = np.array([3, 5, -8])
vector_b = np.array([-9, 0, 4])

Для знаходження векторного добутку використовуємо функцію cross(), якій передаємо наші вектори:

cross_product = np.cross(vector_a, vector_b)
print(f"Векторний добуток: {cross_product}")

Результат:

Векторний добуток: [20 60 45]

Ось ще один приклад:

vector_a = np.array([12, -81, 43])
vector_b = np.array([-30, 11, 57])

cross_product = np.cross(vector_a, vector_b)
print(f"Векторний добуток: {cross_product}")

Векторний добуток: [-5090 -1974 -2298]

Коли векторний добуток втрачає свій сенс

На початку розділу з векторним добутком ми зазначили, що векторний доуток можливий тільки для тривимірних векторів, але давайте спробуємо передати функції cross() двовимірні вектори і подивимося на її поведінку:

vector_a = np.array([5, 3])
vector_b = np.array([10, 2])

cross_product = np.cross(vector_a, vector_b)
print(f"Векторний добуток: {cross_product}")

DeprecationWarning: Arrays of 2-dimensional vectors are deprecated. Use arrays of 3-dimensional vectors instead. (deprecated in NumPy 2.0)
  cross_product = np.cross(vector_a, vector_b)
Векторний добуток: -20

Як бачимо, якщо передати функції cross(), наприклад, двовимірні вектори, то функція обчислює простий скалярний добуток. Тож, можемо зробити висновок, що векторний добуток втрачає сенс у такому випадку.

Також ми бачимо попередження, яке прямо каже, що цій функції у якості параметрів треба передавати саме тривимірні вектори.

Мішаний добуток

Мішаний добуток об’єднує у собі всі попередні і в результаті ми отримуємо вектор.

Формула мішаного добутку виглядає ось так:

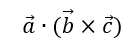
Перший приклад

Для знаходження мішаного добутку ми відповідно будемо використовувати і функцію dot(), і функцію cross():

vector_a = np.array([0, 34, 7])
vector_b = np.array([10, 13, 9])
vector_c = np.array([5, 7, 15])

mixed_product = np.dot(vector_a, np.cross(vector_b, vector_c))
print(f"Мішаний добуток: {cross_product}")

Мішаний добуток: -3535

Другий приклад

Аналогічний приклад:

vector_a = np.array([9, 2, 2])
vector_b = np.array([8, 8, 8])
vector_c = np.array([0, 7, 0])

mixed_product = np.dot(vector_a, np.cross(vector_b, vector_c))
print(f"Мішаний добуток: {mixed_product}")

Мішаний добуток: -392

Висновок

Як висновок ми навчилися використовувати функції dot(), cross() для обчислення скалярного, векторного та мішаного добутку. Крім того, ми встановили головну суть кожного з цих дій над векторами.