Краще читати з комп’ютера, бо на смартфоні деякий текст їде на наступний рядок і це виглядає не дуже…
Енгармонізми, тональності та приключеві знаки
Від супротивного
З появою рівномірної темперації в музиці, підвищення та пониження ступенів(дієзи та бемолі) стали рівними за абсолютною величиною, хоча в Чистих(піфагорійських) строях все було не так.
На скільки знаю, до♯ і ре♭ в останніх перехрещуються(!) і ре виходить нижче. Похибка при цьому доволі мала, її не може почути людина — здається, близько 0.4 цента[¢](1¢= 1/100 півтону). Для інших нот може бути сильніше…
Не зважаючи на це, я впевнений, що й досі можуть бути суперечки, щодо, скажімо, до♯ ≠ ре♭ .
Доля правди в цьому є, якщо в контексті приключевих знаків. Як випадкові знаки це теж має сенс, але чисто як економія — просто треба менше інших знаків, ноти краще читаються.
Відповідно, ми маємо три пари мажорних і три пари паралельних їм мінорних енгармонічно рівних тональності:
Мажори | Мінори |
|---|---|
До♯ і Ре♭ | ля♯ і сі♭ |
Фа♯ і Соль♭ | ре♯ і мі♭ |
До♭ і Сі | ля♭ і соль♯ |
На скільки я знаю, це може викликати плутанину і ускладнити вивчення теорії музики та сольфеджіо.
Тому кожен з вас міг би запитати себе:
А чи є випадки, коли такого не відбувається і енгармонічних тональностей не виникає?
Принаймні за перший обхід квінтового кола…
Так от, я покажу, що таке можливо!
Звичайно, є свої нюанси… Мені допоможе
Принцип Діріхле
або “pigeonhole principle” в англомовній термінології.
Не дивлячись на простоту, штука доволі потужна і допомагає математикам в їхніх доведеннях.
Ось як його можна сформулювати:
Якщо потрібно розкласти 10 голубів на 9 полиць,
то в одній з них точно буде (як мінімум) 2 голуби
Інакше кажучи, якщо потрібно помістити більшу кількість предметів у меншу кількість коробок, то
прийдеться пхати більше 1го предмета хоча б в одну з них.
Повертаючись до музики, що ми маємо ?
Квінтове коло закінчує оберт, коли всі ноти ладу одержать дієз і бемоль.
Є тільки 2 знаки альтерації.
Тональності завжди мають або тільки дієзи, або тільки бемолі.
З кожною квінтою додається чи зникає лише 1 знак при ключі.
А тепер, слідкуйте за руками.
Приключеві знаки можна трактувати як коди або адреси тональностей.
Вони будуть доти, доки є “голі” ступені, тобто без знаку.
З пунктів 3. і 4. можна одержати кількість усіх таких “адрес” :
— Якщо наш лад має 7 ступенів, то буде 7 бемольних адрес і 7 дієзних.
Разом 14, і ніби все!
Але ні, бо є “порожня” адреса, яка відповідає тональностям без знаків.
Тому їх усіх буде: 2 * 7 + 1 = 15.
А тепер згадайте, скільки нот в октаві, — 12. Тому є лише 12 тональностей.
Але адрес-то більше!
Отже, за принципом Діріхле, хоча б Дві адреси будуть відповідати Одному висотному положенню ладу. Чи більше… Без додаткової інформації точно сказати не вийде.
Що ж, тепер все готово! І я можу відповісти на головне питання:
Для того, щоб не було енгармонічних тональностей, потрібно, щоб кількість доступних “адрес” тональностей була рівна фактичній кількості нот.
(які ми розрізняєм на слух)
Можна розписати це більш формально через формули:
2 * k + 1 = N
де N = фактичній кількості нот, а k є довжина/розмір ладу.
Зразу видно особливості:
—По-перше, N може бути тільки додатнім цілим, непарним числом;
—По-друге, це (лінійне) рівняння, а тому N однозначно визначає k. Так що маємо лише один випадок відсутності енгармонічних тональностей.
І це біль, бо решта випадків куди більше. Та й нижче буде показано, що тут виходять не дуже хороші лади/строї…
Виявляється, цього співвідношення достатньо, щоб побудувати певне сімейство прикладів таких ладів. З класичними строями такого не вийде, звичайно, але якщо вийти за рамки 12 півтонів на октаву, то вийде!
Але про це трохи пізніше.
Звідси випливає й інший випадок: якщо адрес буде замало, то нам прийдеться використовувати подвійні знаки — дубльдієзи/дубльбемолі. Тобто лізти у другий “квінтовий оберт”.
Повертаючись до випадків з надлишком адрес, може виникнути ситуація, коли адрес виходить справді багато. Тоді деякі з них можна не використовувати. Частина ступенів може взагалі не одержувати альтерацій одного виду! Тобто було б на багато легше таке запам’ятати. На приклад, третина ступенів може одержати лише дієз, а третина лише бемоль.
А чи може так статися, що нам ще й не прийдеться користуватися двома знаками кожного ступеню? Тобто щоб половина ступенів ладу мала тільки дієзи, а половина тільки бемолі.
Звідси зразу випливає, що довжина ладу має бути парною.
Згідно умови, наших адрес буде разом k/2 + k/2+1 = k+1.
Цього має бути достатньо, отже
k+1 = N .
Знову N є непарним, але вдумайтесь, довжина ладу лише на 1 менше від фактичної кількості нот! Це погано, бо ця дірка в 1 ноту точно буде викликати неприємності. Дуже сумнівно, що це можна використати.
Це точно щось дуже погане.
Однак, якщо дозволити надлишок адрес, — то без проблем. Тоді просто ми самі будемо користуватися лише частиною з них.
Але я сумніваюся, що вдасться обійти осторонь левову частку адрес…
Напевне, якби історія пішла не туди, ми б користувалися пентатонікою як базовим ладом і використовували адреси на його основі.
Тоді за формулою: 2×5+1=11, а всіх 12. Була б одна чи дві тональності з подвійними знаками, а точніше з одним.
І, тим не менш, така система теж підійде! Вона теж дозволяє записати всі класичні тональності, бо використовує ті самі ноти.
З мінусів можна ще сказати, що в пентатоніки менше інтервалів, і тому було б більше всяких варіацій кожного з них: зб._ , зм._ , в._, м._ , ч._ …
В такій системі виникають бемолі при перенесенні ладу на квінту вгору, а дієзи — коли опускаємо. Відповідне квінтове коло, ніби перевернуте.
Це, до речі, можна вивести.
Ремарка про кратність
Бачу необхідним детальніше розібрати випадок з потребою в кратних знаках альтерації. Кмітливий читач й сам розбереться, але зрозуміти мають всі, тому сорі😊.
Тут не буде продовжуватися ідея довгочиту. Це стосується принципу Діріхле в контексті бажаної адресної системи на початку.
Як було сказано, загальна кількість адрес буде (2*k + 1), а нам просто треба вдосталь адрес, щоб мати всі транспонування. Мабуть можна записати це нерівністю:
x*k + 1 ≥ N
де x — якесь ціле число, бажано мінімальне серед розв’язків.
Не складно вивести, що x ≥ (N–1) / k . Округлимо вгору і все.
Ми знаємо, що адреси накопичують знаки спочатку по-одному, а кратні виникають, коли ті ж знаки знову виставляються поверх себе.
Тобто не буде адрес з окремими кратними знаками. Це можливо, хіба що, коли є знаки альтерацій з різною величиною.
Тим більше, перша умова нашої адресної системи
Квінтове коло закінчує оберт, коли всі ноти ладу одержать дієз і бемоль.
призведе до того, що адреси закінчаться тоді, коли всі ступені одержать альтерації найбільшої кратності.
Не забуваючи про те, що кратність буде і в дієзів, і в бемолів — кількість всіх адрес буде
(2*n) * k + 1 ,
де n — кратність, яку ми задаємо.
У кратних знаках є сенс, якщо 2*k+1 замало, тобто довжина вашого ладу закоротка в порівнянні з фактичною кількістю нот (з точністю до октави).
Так, основне, що нам потрібно — щоб адрес було достатньо, тому має виконатися нерівність
(2*n)*k + 1 ≥ N
Але може бути забагато адрес при даному n . На приклад, для n=3 і 7-ступеневого ладу буде аж 2*3*7+1=43. Такого для ділення октави на 31-ну рівну частину трохи забагато. Хіба ділити на 43 😅.
Тому можна шукати найменше число. Нехай x = (2*n) ,
маємо тепер таку нерівність:
x*k + 1 ≥ N , мінімізувати x
Звідси маємо:
x ≥ (N–1) / k
Дріб з права часто не буде цілим, але якщо буде — можем брати x = (N–1) / k .
В інших випадках можем округлювати вгору:
x = ⌈ (N–1) / k ⌉
Такі пів-квадратні дужки — вже стандарт позначення округлення:
де гачки — туди і округлення. Для округлення до найближчого цілого можуть написати з гачками в різні боки ⌊…⌉ або ⌈…⌋ (не пом’ятаю, яке).
Далі зворотня підстановка і обчислюємо n :
x = 2 * n,
n = x / 2
Знову значення може бути дробовим, тому можем округлити вгору:
n = ⌈ x / k ⌉ ,
а якщо комбінувати формули — буде трохи страшно:
n = ⌈ ⌈ (N–1) / k ⌉ / k ⌉ ,
дужки округлення не розкриваються нормально, тому так і буде.
Але я впевнений, що можна не паритися і підібрати n вручну, бо на практиці не буде великих чисел, хоч математика й не складна.
Ось вам і метод, як визначити макс.кратність знаку для потрібної (оптимальної) адресної системи.
Коли 2k+1 замало.
Хоч я й сумніваюся, що використання невеликої кількості адрес з кратностями — не потягне за собою їх усіх аж до максимальних …
(теоретики мене зрозуміють)
Бонус
Навіть можна порахувати, скільки ступенів з макс.знаком буде найбільше серед оптимальної кількості адрес.
— Кратності додаються тоді, коли минулих замало.
Отже, достатньо підібратись до N тією ж формулою, просто знизу:
y*k + 1 ≤ N, максимізуючи невідоме y .
Тоді різниця між ними дасть недостачу, яку потрібно заповнювати адресами з більшими кратностями. А оскільки в нас є бемольні та дієзні адреси, цю недостачу можна поділити навпіл порівну з кожним видом знаків:
( N – (y*k+1) ) / 2 — найбільша кількість знаку макс.кратності/адресу
На перший погляд, цей дріб може повертати дробове число, що дасть неоднакову кількість бемолів і дієзів макс.кратності. (не проблема — завжди можна додати лишню адресу)
А для того, щоб дріб був нецілий — N і y*k повинні мати однакову парність. Якщо не дуже вдаватися в підбір хороших k та y , ми вільні вибрати просто якесь (ціле) число менше N, тієї ж парності, але яке є добутком двох (тобто складене).
На приклад:
N = 41, y*k=39 (k=13, y=3), маємо 41–39–1=1 ;
N = 22, y*k=18 (k\y : 9\2 чи 6\3), маємо 22–18–1=3 .
Якщо відомо x , то y = x–1 оскільки x = ⌈(N–1) / k ⌉, а y — має бути округленням вниз ⌊ (N–1) / k ⌋. N затиснуте між ними:
y*k+1 ≤ N ≤ x*k + 1
z = (N–1) / k точно посередині, це розв’язок рівняння z*k + 1=N.
Якщо рівні, то всі ступені заповняться, все буде точно і відповідатиме випадку з основної теми довгочиту. (різниця = 0)
А якщо відомо, як далеко потрібно зайти в кратне “квінтове коло”, то це дає нам кількість адрес, рівну кількості нот. Тобто виконується умова відсутності “енгармонічних” адрес.Тоді що, ціль довгочиту досягнуто?
— ніби й так, але тут використовуються не всі адреси.
Випадок рівності, яку нижче розглядають в деталях:
2 * k + 1 = N
дає систему, в якій взагалі всі адреси потрібні. Створили всі першої кратності і нічого не треба відкидати.
Аналогічно для кратностей:
(2*n) * k + 1 = N
Інсайд
Усе це ніяк не стосується того, на скільки великими/сильними є діези/бемолі ! Але важливо, щоб була лише одна абсолютна величина, спільна.
Оскільки можливо мати випадки з різними. Про це трохи сказано нижче.
Повертаючись до основної теми, давайте тепер виведем всі фактори, які впливають на аналогічну квінтовому колу систему. Це дасть спосіб створювати приклади, про які йшлось вище.
Пульт керування “квінтовим” колом, темперована версія
Для цього згадаємо про ділення з остачею, яке записується по-різному(в залежності від знань у програмуванні), але математичним стандартом є такі :
5 mod 4 = 1,
що також рівне ( 5/4 − ⌊5/4⌋ )*4 , де ⌊…⌋ — ціла частина(floor);
5 ≡ 1 (mod 4)
Останнє — більш модерний спосіб, який встановлює порівняння чисел, які дають однаковий залишок від ділення на певне число. Тут це 4.
Його плюс в тому, що число зправа може бути любим того ж типу, не обов’язково, щоб воно було рівне остачі від ділення. Тут може бути 13.
Це не буде мати великого значення, але я можу використати його пару разів.
Що ж, нам потрібно перекласти ситуацію з тональностями на чисту математику. Ось як це можна зробити.
Модель і результати
Без втрати загальності, представимо ноти, як абсолютну висоту в півтонах від тоніки(І ступінь): 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11.
Починаємо з 0, бо інтервал Прима фактично не має розміру.(якщо чиста)
Буде трохи плутанина, бо виходить однаково як для нот, так і для інтервалів. Але це добре в нашому випадку.
Всі ці числа можна вважати остачами від ділення на 12. Тому будемо дивитися на них саме так.
Це дозволить виконувати операції додавання і множення між ними, не виходячи за рамки їх сенсу.
А як це?
— з точністю до порівняння за остачею.
На приклад, 5+7=0 , бо 5+7=12 , а 12 mod 12 = 0, вочевидь.
Виходить, що 5 і 7 є протилежними остачами, аналогічно парі протилежних чисел.
Але насправді, можна зробити так, що 7 буде рівне (−5), все-таки 12−5=7.
Тобто це лише певна формальність, використання додатних остач…
Множення теж можна: 2×8=4 , бо стандартно 2×8=16, а 16 mod 12 = 4.
Тільки виникають і відмінності від звичайних чисел, на приклад:
—зазвичай 3×8=24, тому в системі остач (mod 12) це буде 0.
Задумайтесь, добуток 3×8 як остач від ділення на 12 повертає 0.
Хоча, 3+2=5, 8+1=9 навіть як остачі, і тому ні 3, ні 8 не є нулями!
Математично просунуті читачі зразу зрозуміють, що через це в такій,
арифметиці остач (модульній арифметиці) загалом
— неможливо вирішувати рівняння типу
ax = b
Бо якщо я захочу, скажімо 2х = 9, то розв’язку не існує.
А навіть, якщо 2x = 8 ще якось розв’язати можна, то це все одно дуже натягнуто… все-таки хочеться, щоб 8/2 = 8×½ , але ½ є
рішенням рівняння 2х = 1 , а воно не розв’язується, ½ не існує.
Ну і це відбувається через те, що 12 ділиться на 3, а з 8-кою є спільний дільник.
Так от, таким способом маємо квінту розміром в 7 півтонів, а як ступінь це V ступінь ладів мажору/мінору .
Випишемо ці лади в термінах остач:
Мажор | Мінор |
|---|---|
0, 2, 4, 5, 7, 9, 11 | 0, 2, 3, 5, 7, 8, 10 |
Тепер, любе висотне положення можна одержати просто додаванням до кожного значення в цих послідовностях любої з 12ти остач, як паралельне перенесення. Арифметика все зробить за нас. Тільки от, де дієз/бемоль ми не побачимо, чи таки можемо?
Якщо подумати, то нам достатньо порівняти минулу послідовність і майбутню(перенесену). Так буде видно, які ноти зникли, а які з’явилися.
Це не дасть нам сильно великого плюсу, але практика показує, що часто ноти співпадають, хоч їх роль і номер інші.
Спробуємо так зробити з переходом у тональність IV ступеню(До→Фа):
(0, 2, 4, 5, 7, 9, 11) → +5 = (5, 7, 9, 10, 0, 2, 4)
Як і має бути, співпало 6 нот: 0, 2, 4, 5, 7, 9 . А 11 зникло,
на його місці тепер 10. Здається логічним, що 10 це просто (11−1).
Так що метод працює, нічого особливого, просто використовуються інші позначення.
Напевне це буде працювати завжди, не треба лізти кудись далеко.
Можна побачити пару мінусів:
—треба все перебирати;
—послідовності нот-остач(лади) не виглядають особливими, — не видно, як їх робити.
Але якщо змінити кут огляду, то все стане зрозуміло.
Додаванням знаків керують перенесення на квінту, вона відповідає остачі 7.
Але 7 і 12 не мають спільних дільників! Відповідно, всі кратні 7 числа можуть дати любий залишок від ділення на 12.
Отже, і рівняння 7x = 1 має розв’язок. На 7 можна ділити ! Ну, і на 5, 11 теж можна. Разом з 1 це всі оборотні остачі (mod 12).
В принципі, й так було відомо, що можна розташувати всі 7 нот по квінтам.. Але тепер є зачіпки до узагальнення цієї штуки!
Залишився лише 1 крок. Давайте розташуємо ноти-остачі в порядку квінт, тобто просто візьмемо остачі від добутків старих на 7:
(0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11)→ ×7 = (0, 7, 2, 9, 4, 11, 6, 1, 8, 3, 10, 5)
Подивимось, де знаходяться ступені класичних ладів:
Мажор | Мінор |
|---|---|
0, 7, 2, 9, 4, 11, −, −, −, −, −, 5 | 0, 7, 2, −, −, −, −, −, 8, 3, 10, 5 |
ОПА! Щось вимальовується.
Ноти, які не ввійшли у послідовності(лади) формують ряд послідовних кратних числа 7 (з точністю до залишку).
Але хай вам не виглядає, що решта остач не формують такі ж ряди.
Якщо їх трохи продовжити, це буде видно зразу:
Мажор: 0, 7, 2, 9, 4, 11, −, −, −, −, −, 5, 0, 7, 2, 9, 4, 11, …
Мінор : 0, 7, 2, −, −, −, −, −, 8, 3, 10, 5, 0, 7, 2, …
Враховуючи факт існування паралельних тональностей, ряд для мінору можна перенести так, щоб його значення співпали з рядом мажору, тільки порядок зміниться.
(початок з 9, бо 9 відповідає VIст. або ноті ля, якщо I=до)
І що з цього можна одержати?
Дивіться, в нас й так шкала квінт, тому рух по квінтовому колу, це просто зсув ряду на ту чи іншу кількість позицій.
1 позиція — 1 квінта
Зразу буде видно, скільки нот співпало, а які зникли.
Можна теж бачити, які ноти одержать знак і який саме знак.
Подивимось на малюнок:
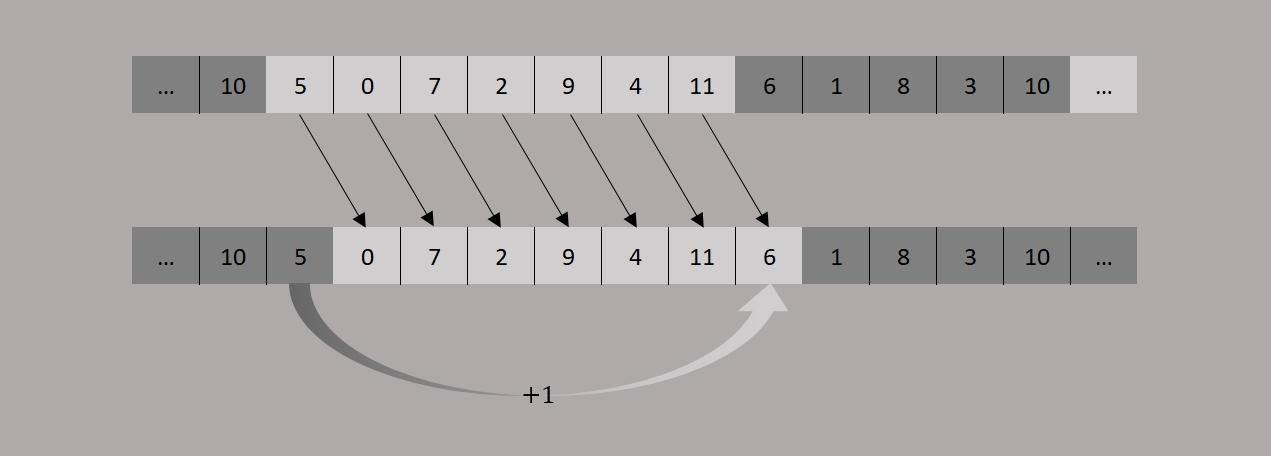
Тут маємо мажор і зміщення на квінту вправо(нижній).
5 зникла, але можна вважати, що 6, яка з’явилася, — є підвищеною 5, тому вказано стрілкою, що виконали +1, тобто дієз.
Видно, що з кожним кроком спільних нот меншає, а ми маємо приріст нових по одній.
Різниця між наступною новою і останньою лівою(що зникне) буде завжди однакова і рівна +1. Це і є наш дієз.
Думаю, аргументів достатньо, щоб зробити висновок:
—Тільки в такому випадку система “адрес” “тональностей” буде аналогом квінтового кола.
І це завдяки тому, що лад вибудовується в отакий “зв’язний” ряд/діапазон послідовних кратних квінти.
З точки зору модульної арифметики це відповідає тому факту, що на послідовності квінт 7 кроків відповідають одиниці, бо 7×7 ≡ 1 (mod 12).
Узагальнюючи це, маємо необхідну, але недостатню умову:
Довжина ладу має давати остачу, обернену до остачі керуючого інтервалу(квінти).
А для достатності потрібна “зв’язність”, бо інакше буде дещо інше. Про це далі.
Які вийшли кнопки?
З малюнку зразу випливає три ефекти, які виникають при зміні параметрів таких “смуг” :
— Зміна порядку.
Різниця між наступною нотою(типу 6) і старою(типу 5) при перенесенні на “керуючий” інтервал(квінту), як вище, − може бути (–1). Достатньо просто змінити довжину смуги на таке значення x, що 7х ≡ −1 (mod 12). Оскільки 7 оборотне, то розв’язок існує.
Він рівний (−7), або 5. Від’ємних довжин нема, правда? Ось вам і перевернуте коло для пентатоніки!
—Зміна базового значення/розміру альтерації (на задане значення).
Фактично, потрібно, щоб різниця між зниклою нотою і новою була рівна заданому значенню. Тут достатньо змінити довжину, нам просто треба вирішити рівняння 7x ≡ const (mod 12) .
А загалом, замість 7 може бути люба оборотна остача. Легко узагальнити.
Примітка: попередня властивість є частковим випадком цієї.
—Збільшення кількості знаків альтерації за 1 крок.
Тут достатньо порвати смугу на 2 чи більше частин. Викинемо хоч якусь ноту посередині і будуть додаватися вже по дві альтерації за кожен зсув на “керуючий” інтервал(квінту).
Ось тому-то й потрібна “зв’язність”.
Я сильно з цим не бавився, але здається, можна одержати ситуацію, коли ці дві альтерації будуть різного напряму: одна дієз, інша бемоль. І обидві ще й різного розміру!
Мабуть тут грає роль довжина кожного кусочка, бо для них будуть справедливі властивості вище, тому може бути щось ну Дуже специфічне!
Можна так посунути, що обидва правила накладуться і будуть якісь дивні дубль-знаки, які будуть одержані накладанням кількох, навіть різного напряму.
А таке буде чимсь Дуже складним у вивченні.
Добре, що так не сталося, правда?
Додатково
В якості бонусу можна обчислити остачу, яка визначає перший ступінь ладу за формулами:
7×(кількість дієзів) mod 12 = (тоніка)
5×(кількість бемолів) mod 12 = (тоніка)
бо бемолі протилежні дієзам, вони понижують на 1, тобто додають (−1)
ну і 5 ≡ −7 (mod 12).
Через те, що є паралельні мінори, можна одержати тоніку паралельного мінору як зсув тоніки мажору: відніміть 3 від остачі тоніки. Для інших випадків може бути інакше. (Здається нічого не переплутав.)
Надіюся, зрозуміло, що кількість дієзів/бемолів не має перевищувати 7, бо ми перейдемо на друге коло.
Тут є мінуси, бо якщо тоніка сама є дієзом/бемолем, то це можна визначити тільки за бажанням — треба знати чи дієзна, чи бемольна тональність.
Тому я їх так розділив.
А ще, ці рівняння дозволяють дізнатися, скільки альтерацій додається чи віднімається при переході до іншої тональності від поточної.
З правого боку — інтервал перенесення, тобто скажімо:
7x mod 12 = 3 (мала терція). Наше завдання — знайти x=3/7, а це 9 у такій арифметиці.
Тобто якою б не була поточна тональність, при перенесення на інтервал 3 (вгору), нова матиме на 9 дієзів більше. Не дуже приємно мати подвійні дієзи, бо 9>7 (довжина ладу). Отже, краще взяти бемолі, тобто рівняння:
5x mod 12 = 3. Звідки x=3/5=3/(–7) = 0 – 3/7 = 12–9 = 3. Справді, 3×5 mod 12 = 3.
Три бемолі краще, ніж 9 дієзів, правда?
Паралельно ви дізналися, що можна обрати кращу адресу : замість додавання дієзів можна їх відкидати — стільки, скільки бемолів треба додати.
Десь вище було сказано, що бемоль це від’ємний дієз. Додавати бемолі це як раз віднімати дієзи, а якщо 0 дієзів, то будуть лише бемолі. З дієзами навпаки.
☝️Основне — не забути послідовність додавання і тих, і тих ! 😅
А тепер, нарешті, я можу дати приклад, які ж такі лади не мають енгармонізмів!
Бо стало зрозуміло, в якому випадку лад дозволяє аналогічну квінтовому колу систему “адрес” в батьківському темперованому строї.
Це буде тоді, коли його довжина рівна числу, яке дає остачу, обернену до керуючого інтервалу. А вже його можна обирати за бажанням, основне його оборотність в системі остач по модулю розміру рівномірної темперації.
Можливо, можна спробувати обирати керуючий інтервал з міркувань додавання мінімального числа знаків при транспонуванні ладу на нього…
Сам же ж лад має бути множиною послідовних кратних керуючого інтервалу. Така цілісна “смуга” без дірок.
Навіть можна сказати, що це має бути арифметична прогресія, правда?
Якщо ми її порвемо, то це вже щось… з двома різницями, як мінімум.
Застосування
Отже, я закінчив на формулі з принципу Діріхле.
Фактична кількість нот має бути рівна числу “адрес” “тональностей”:
2k+1=N
Нагадую, що k є довжиною/розміром шуканого ладу(послідовності).
Звідси маємо: k=(N–1)/2 . Але це тільки загальний розмір ладу.
А, як було визначено вище, це має бути обернена остача до керуючого інтервалу. Позначимо його m. Нам і потрібно його знайти.
Тобто має виконатися mk ≡ 1 (mod N).
В такому разі буде найпростіша альтерація +1/–1 і вони будуть з’являтися по-одній.
Перейдемо до остач (mod N). Тоді
2k+1 ≡ 0 (mod N)
Підставимо mk замість 1:
2k+mk ≡ 0 (mod N) , k виноситься:
k(2+m) ≡ 0 (mod N)
Тут можливо 3 випадки: k=0, але k не може бути 0 !
m=(–2) або що те саме (N–2);
або випадок, коли k i (2+m) ненуньові, тобто є дільниками N або кратних йому чисел.
Однак, як би це не було заманливо, mk=1 тому k теж оборотне, як і m. Так що третій випадок неможливий, бо оборотні остачі дають 0 тільки тоді, коли множаться на 0.
Залишається лише один розв’язок!
m=(N–2)
Що ж, N це розмір темперації, — скільки рівномірних поділів октави ми маємо. А керуючий інтервал вийшов Аж на 2 “поділки” меншим за октаву.
І чим більше N, тим він ближче до октави. Відповідно, виходять такі собі різні… септіми? А це доволі дисонансні інтервали, ну якщо N велике.
А це вже не дуже добре…
Візьмемо для прикладу N=9. Маємо інтервал в 7/9 октави, тому він матиме дійсну величину в 2^(7/9) що дорівнює близько 9⅓ класичного півтону.
Тобто трохи більше за класичну велику сексту. (Семізбільшена секста?)
Але це лише один з двох обернених інтервалів, як квінта і кварта.
Тут обернений буде, вочевидь, 2⅔ півтону. (Семізменшена терція?)
Давайте тоді таки побудуємо цей приклад, хоч він і буде мати всього..
(9–1)/2 = 4 ступені :
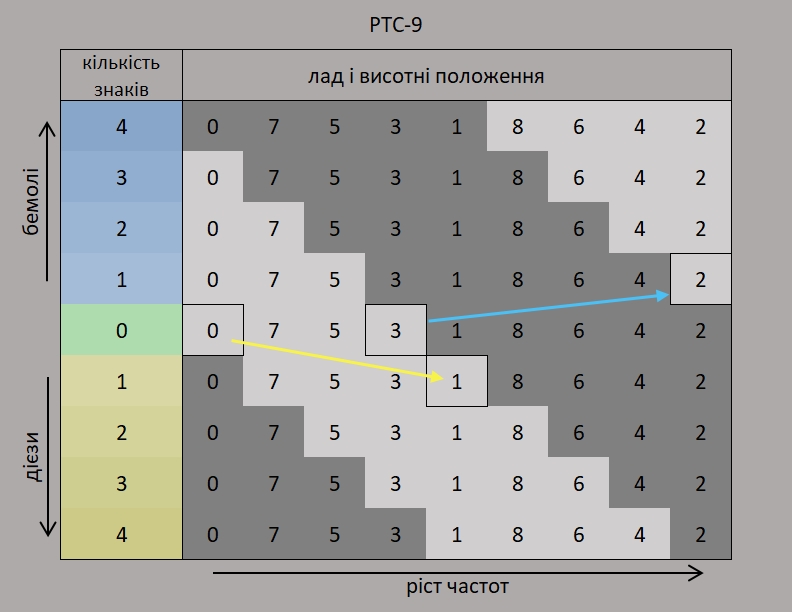
Все працює прекрасно, тільки дієзи починають виставлятися зразу з тоніки, що не дуже. А бемолі, як видно — з II ступеню.
Це не проблема, можна обрати любе положення за початкове. На приклад, можна взяти за аналогією — від 2, там де 1 бемоль. Чому? Бо у класиці мажор починається з 5, а 5 це фа, а фа-мажор має 1 бемоль.
Також зразу кидається в очі той факт, що його розмір завжди буде менше половини всіх нот, — батьківського темперованого строю.
Буде більше “чорних клавіш”, ніж білих.
У природньому розташуванні:
0, 3, 5, 7, 0…
Зразу можна вивести пару властивостей:
—через те, що додається (−2), парність остач зберігається.
Звичайно, поки ми не перевищимо N;
—має будову 3222 , де за одиницю вважається 1/9 октави.
Ці найменші інтервали матимуть розміри 2⅔ та 4 (!) у півтонах.
Так що цей лад містить класичну велику терцію…
Не думаю, що при збільшенні N буде щось суттєво змінюватися..
Сама інтервальна будова теж буде подібною:
N=11 → 32222
N=13 → 322222
N=15 → 3222222
…
це справді так, я перевірив заднім числом, але краще пізно, ніж ніколи.
Зробив трохи візуалізації на desmos , можете трохи покрутити параметри, але я не додав опції рвати послідовність.. Сумніваюся, що вийде зручно, треба розібратися.
На жаль, на Друкарні нема як приклеїти невеликі звукові доріжки в довгочити, тому буде без семплів. Але їх можна додати на зовнішньому ресурсі. Desmos має опцію програвання графіків, тому його і можна використати.
готово : туди (тільки цільові строї, але звуки — “синусоїди”.. на жаль).
Можу тільки сказати, що звучать усі ці лади не дуже цікаво. Для програвання я використовував програму Scala.
Зате! Можна почути, що вони подібні на класичні лади мажору та цілотонового звукоряду, містять якісь фрагменти пентатоніки та версії “пентатоніки” з … 7 ступенів. Просто звучання схоже.
І чим більше N, тим меншим буде інтервал у 2 “півтони”.
Так що, з якогось номеру відстані будуть доволі малі, а тому не відрізнятимуться від РТС-у(рівномірна темперація). Тоді можна буде грати довільний лад з достатньою точністю. Але для цього треба велике число N.
Не пробував його шукати…
А давайте.
Людина може чути в середньому, різницю між інтервалами у 5 центів(1/240 від октави). Тоді, якби двійка відповідала 5 центам і будова ладу складалася лише з двійок, то було б 240 двійок і N було б =480, але через трійку на початку всі двійки мають бути трохи менші.
В принципі, якщо довжина 240, то за формулою (N–1)/2 маємо N=481. Це дасть двійку розміром трошки менше 5 центів: ≈4.98961¢.
Якщо взяти N=479, то теж непогано, там двійка буде давати ≈5.01¢.
Беручи менші непарні числа, можна побачити, що відхилення росте не дуже швидко. Для N=461 наш найменший інтервал буде всього ≈5.2¢.
Підсумуємо результати
За допомогою принципу Діріхле було показано, що відсутність енгармонічно-рівних “тональностей” можлива, однак тільки в одному випадку, коли 2×(довжина ладу)+1=(фактична кількість нот).
Або коротше 2k+1=N.
Було виведено всі параметри для керування аналогами “квінтового кола”.
—Можна змінити (базовий) розмір альтерації, а як частковий випадок перевернути порядок додавання знаків відносно перенесення ладу(вгору бемолі, вниз дієзи).
—Можна змінити кількість знаків, які додаються кожного разу. Це число не змінюється; Сюди ж : контролювати розмір і тип кожного.
Для того, щоб все було максимально класично
(1 квінта — 1 знак, розміру 1)
потрібно, щоб
—лад мав розмір, який давав оборотну остачу при діленні на порядок батьківського РТС-у;
—вона має бути оберненою остачі аналогічного квінті інтервалу(він керує додаванням знаків);
—сам лад має бути арифметичною прогресією останнього, в арифметиці остач.
Користуючись цим, було побудовано сімейство ладів/строїв, які мають властивість відсутності енгармонічно-рівних положень цих ладів.
Звичайно, за перший обхід квінтового кола.
Всі вони мають форму 32…2 і мають довжину (N–1)/2, де
N є непарним числом і порядком РТС-у, де живе наш лад/стрій. (N можна одержати сумою чисел у 32…2 .)
Керуючий інтервал і йому обернений відповідно рівні (N–2) і 2 в термінах цього РТС-у.
Читачеві прийдеться повірити мені на слові, що ці строї звучать подібно до деяких ладів, серед яких бувають якісь аналоги цілотонового, а також натурального мажору. Всі звучать, ніби їх грають на розстроєному інструменті. Загалом — доволі бідні. На приклад, якщо N=23 то виходить 11 ступенів і воно справді схоже, ніби я викинув 1 ноту з РТС-12.
Можливо, з використанням знаків альтерації все стане трохи краще.
Зрештою, наступні два РТС-и, які теж добре(і навіть краще) наближають класичні строї мають як раз непарний порядок: це РТС-17 та 19.
Для порівняння, стандартний — це РТС-12, в ньому шуканих ладів немає.
Висновок
Унікальність ладів з відсутністю енгармонічних адрес(приключевих знаків), погане звучання і бідна гармонія прикладів з такими властивостями
— роблять їх використання дуже сумнівним.
Тому й виходить, що інші випадки кращі, але вони будуть мати енгармонічність в тій чи іншій формі: то недостатньо 1 “квінтового” оберту, то забагато варіантів приключевих знаків. От і виходить.
Отже, її не обійти стороною без інших наслідків.
Однак, достатньо велика надлишковість адрес може бути корисною через те, що якісь із них можна не використовувати. Таким чином можна влаштувати все так, щоб деякі ступені/ноти не одержували або дієз або бемоль. Максимально можна мати ситуацію, коли достатньо дієзів однієї половини ступенів та бемолів для іншої.
Тоді питання на рахунок “до♯ ≠ ре♭” або “до♯ = ре♭”
— вже просто не будуть виникати(!), хіба хтось захоче решту адрес використати…
От тільки для цього треба, щоб виконалась умова k+1=N , де k є довжиною ладу, а N є розміром/порядком РТС-у.
Так ще гірше, ніж лади, про які йшлося вище…
Єдиний варіант, як це все може стати хорошими ладами
— змінити обчислення інтервалів!
Зазвичай за період строю(октаву) беруть відношення частот звуків 2:1 , і частоти нот строю будуть 2^(x/N) але можна перейти до іншої основи, на приклад 3 (тритава) чи іншого простого числа типу 5, 7, 11, 13, 17, 23, 29…
Ніде вище не було ніякої заборони на це.
Будуть і свої проблеми, на приклад — не буде чистих(точних) октав.
Залишу це завдання на потім. А читач може спробувати самостійно.
Дякую за увагу і
Слава Україні!
P.S. Я мабуть, тобі збрехав
Після вельми тривалого часу стало зрозуміло, що мотиваційні пропозиції з початку довгочиту все-таки погані. Там було про окремі ноти, а потім перейшли до цілих ладів/тональностей. Це трохи нечесно.
Якщо так, тоді вірніше говорити про енгармонізми ступенів.
Тут в принципі, не тільки тональності підуть, а любі лади.
Кмітливий читач, трохи подумавши, може сам зрозуміти, що попри існування “квінтових кіл” без енгармонічних “тональностей”
— енгармонізми між ступенями(різних номерів +)
будуть справді завжди.
Обійти їх можливо лише у найгіршому і зовсім нереальному прикладі
з точки зору муз.теорії.
Справа в тому, що ми можемо побудувати любий лад від звуку, з I ступеню.
Це можна уявити, як відрізок і точка, відмічена на ньому.(в нас початок)
Очевидно, що в нас буде обмежене число можливих позицій для першого ступеня. Тому коли ми розглянемо всі такі положення, то деякі будуть перекриватися.

Так, перші ступені можуть бути унікальними, але вони не одні, до них приклеєно цілий відрізок! В нас не точка, в нас певна область навколо неї. Той самий принцип Діріхле :
— або розташувати відрізки без перекриття і пропустити якісь “тоніки”
— або мати всі “тоніки”, але лади/тональності будуть перекриватися.
Наша модель “квінтового кола” вище теж своєрідно впорядковує всі можливі ноти вздовж прямої. Отже, тут теж буде спостерігатися перекриття. Як наслідок ми на прикладі помітимо, що в нас буде хоч одна нота ладу, яка є зразу в двох: в одному одержана як підвищений ступінь, а в іншому як понижений.
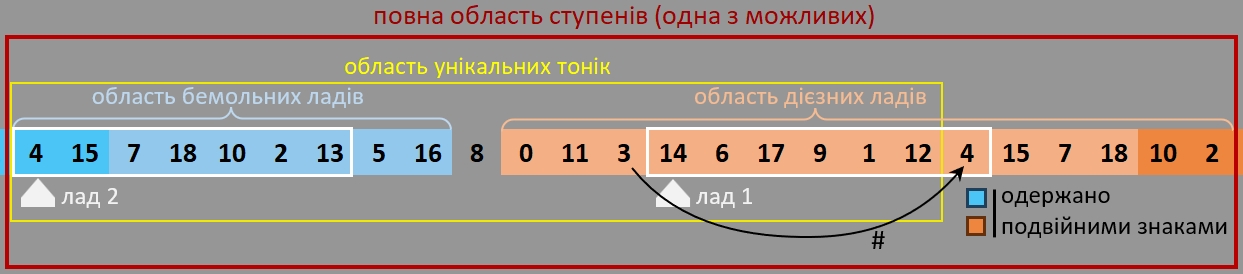
На схемі вище зображено приклад для ділення октави на 19 рівних частин, щоб було багато місця.
В такій системі 11/19 октави дає непогану квінту(∼7¢ похибка), тому не гріх скористатися натуральним мажором для прикладу вище.
Ви спостерігаєте аналог того самого квінтового кола, тільки більший.
Білими стрілками вказано стартову ноту. Будем думати це тоніка.
Тоді, починаючи з остачі/висоти 8 ми можем симетрично сунути її поки не пройдемо любу іншу. Всіх 19, отже по 9 наліво-направо. 8 порахували.
А вже від кожної берем 7 кроків і маємо наш лад.
Тут видно, що переміщення тоніки на 4 і на 14 мають одну і ту ж ноту(4), але у правому(лад1) це якийсь дієз (10 квінт від 8), а в лівому це (дубль-)бемоль.
Лад2 має подвійний бемоль, бо ми так обрали тоніку — з лівого краю смуги ладу(по квінтах). Якби ми брали ноту посередині смуги, то подвійний знак попав би не на тоніку. Ось, як це могло б виглядати:

Тепер все ясно, позбутися енгармонічних ступенів означає, що
— лад має складатися лише з однієї ноти (тоніки).
Тільки тоді, математично, в нас не буде накладань.
Іншими словами — лад не вилазить за межі жовтої області.
Ось чому це “ найгірше з точки зору муз.теорії ”.
Може здатися, що у першому випадку дубль-дієзи виникають суттєво пізніше, але це ілюзія.
Кількість квінт зсуву, необхідних для 2-кратних знаків залишається незмінним. (І взагалі для заданої кількості)
Згадай стару частину цього довгочиту.
На останньому малюнку лад2 має тонікою 13, а не 4. Вийшов інший зсув.
Тим не менш, ті ж множини таки мають тепер інші знаки, все-таки тоніка ладу2 ближче до 8. Проте абсолютна відстань між тоніками лад1 і лад2 тут і вище залишається незмінною : ±13 квінт.
