Як якось ввечері зробити велике відкриття?

Кілька слів від автора

Цей матеріал є перекладом і текстовою адаптацією на основі відеоролика. Я прикріплю джерело в якості бібліографії.

Лайфхак:
з темною темою сайту читати краще)
текст було виконано під неї, так що… вибачайте за незручності.

Передмова

В цьому відео хотів зробити такий цікавий експромт, який стосується генезису відкриттів.
Як випадково і глибоко може пробрати якусь людину, хто просто так у вільний час пробує, дивиться на якісь формули.
Тут хотів поговорити про компл‵ексні числа і формулу Ейлера(Ойлера).

Ідея та гіпотеза

Давайте уявимо себе таким персонажем, хто цікавиться математикою і любить в ній порпатися).
І ми з вами в черговий раз, надвечір сідаємо за стіл, повний записів минулих задач і може навіть "досліджень".

І от ми дивимося на формулу синуса для суми кутів:

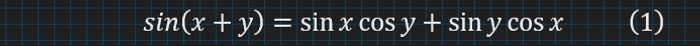
І що? Формула та й формула, нічого особливого Ну, є якась симетрія…
Але нехай так сталось, що ми побачили біля себе формулу для степеня з сумою показників:

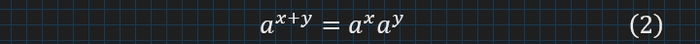
Якщо придивитися, ми побачимо що в першому, ніби, сума перетворюється в добуток, при чому на два добутки. У другому тільки один добуток, але обидва випадки здалися схожими…
Згадується, що синус і косинус - дуже пов'язані функції. Якщо ми змістимо синус на 90 градусів, то одержимо косинус. Я про тотожність

Тобто у формулі (1) написано "щось синусоподібне (х) на щось синусоподібне(у) + синусоподібне (у) на щось синусоподібне(х)".
Можна подумати, що між цими формулами таки є якась аналогія:
синус поводить себе трохи схоже на показникову функцію, бо переводить “суму” в “добуток”.

Тоді ми могли би подумати…
А може є якесь невідоме ε (гр.[епсилон]) яке при піднесенні в степінь x  дає нам щось подібне (1)? Проте, там змішано синус і косинус… Тоді не чисто синус, а суму синуса і косинуса, помножених на якісь множники.

От нехай нам так просто захотілося! От ми сиділи ввечері, думали над формулами і помітили таку "симетрію".
Маємо гіпотетичне рівняння:

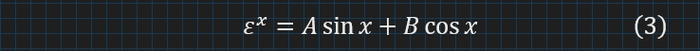
Де А, В і ε − невідомі константи. А далі, дивлячись на формулу (1) − пробуємо знайти їх, щоб все зійшлося.
Все-таки аналогія явно відчувається.

А 𝒾 Б

Щоб усе зійшлось, мабуть потрібно застосувати формулу (1), тобто у виразі (3) замінимо x на x+y:

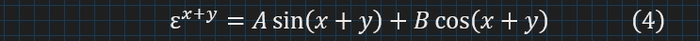
Розпишемо тригонометричні функції суми кутів, як синус із (1):

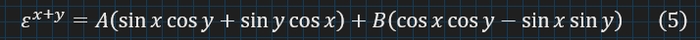
Формула для cos(x+y) — відома, тому ми її підставили. Розкриєм дужки:

А як далі? Можна розписати ліву частину рівняння згідно (2):

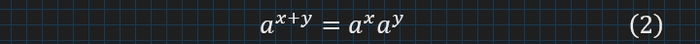
До речі, ми знаємо чому рівне εˣ , а як наслідок і εʸ . (3)

Розпишемо цю ліву частину окремо:

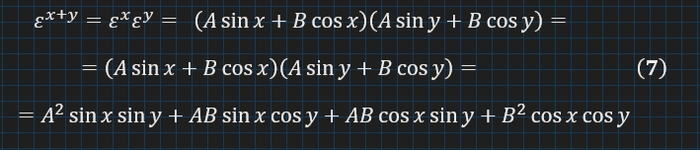
Поки що ми просто пробуємо, дивимося на наслідки зі своїх гіпотез.

Тепер у нас має бути :

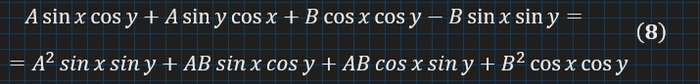
(Я поміняв місцями ліву і праву частини, так зручніше. Помилки нема.)
Тепер достатньо підібрати множники при однакових доданках по обидві сторони рівняння.
Читаючи (8) зліва згори, спочатку можна одержати A=AB , звідки B=1, очевидно. Далі можна одержати  B=B² , що виконується, коли B=1 .
Але в кінці маємо −B=A²  .

Тобто  A²  = −1  !!

Такого у дійсних(звичайних) числах не може бути, однак, як це завжди було в математиці - хтось просто вводив подібне “неможливе” без необхідного доведення і продовжував виводити теореми, може щось хороше й вийде.
І нехай для зручності, ми просто так захотіли позначати значення А через 𝓲 . Навіть могли б назвати її “уявне” число, “уявна одиниця”.
Можливо, як для винахідника, для нас 𝓲 може бути просто деяким особливим буквеним виразом. Так ми й будем з ним працювати пізніше.
Пам’ятаєм, що 𝓲² = −1.

Ось ми, фактично й перевідкрили компл‵ексні числа! Але не зі сторони рішень квадратних і кубічних рівнянь — прямо, а дещо іншим шляхом.

Тепер А і В відомі, можемо підставити у (3), маєм рівняння (9):

Якщо ж ми вже ввели "неможливе число" 𝓲 , то вже не будемо сумніватися в існуванні ε . Йдем ва-банк!

Тільки вдумайтесь, - ми можем обчислити степінь шляхом обчислення, грубо кажучи, суми синуса і косинуса від її показника, а точніше лише пари* цих значень.

невеликий відступ

Далі автор оригіналу використовує теорію границь для ще глибшого занурення у природу ε , але ми можемо не знати цієї теорії, тому ми могли б скористатися тим, що в нас є.
І справді − відповідь перед нами, бо є властивість: a¹ = a . Тому маємо :

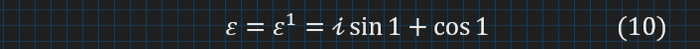
На цьому ми могли й закінчити, ввівши своє число з особливими властивостями). Однак, працювати з ним в такому вигляді може бути невигідно... хоча, якщо розкладати степінь цієї суми як біному(двочлена), то можливо, вийде одержати деякі тотожності з тригонометричними функціями. З формули (9) навіть краще буде.

Останній штрих

Залишилося тільки знайти ε .
Ми запитуємо себе про спосіб його пошуку. І зі знаннями теорії границь (і так званих Першої та Другої чудових границь) пограємся в таку-собі гру.
Я не буду коректним у викладках з границями, але насправді це можна пізніше зробити вірніше.

Згідно першої чудової границі маємо можливість замінити
sin(x) на x для достатньо малих значень x , а от cos(x)≈1 , коли x достатньо малий. Маємо суттєве спрощення:

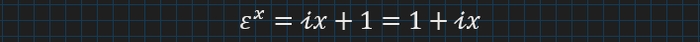
Але любе число можна зробити достатньо малим, якщо розділити на якесь велике число. Давайте розпишемо x , як n∗x/n , де n − дуже велике, а x/n буде дуже малим, а n скорочується, однак…
Згадаємо, що степінь з добутком показників − не що інше, як степінь степеня:

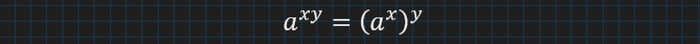
Маємо:

Якщо  відправити n на нескінченність, то ми зможемо хитрим способом обчислювати любі степені ε. Нескінченність гарантує необмежений ріст точності. Але ви завжди можете знайти таке n , щоб обчислити вираз з любою даною наперед точністю. А нам треба точно).
Буду записувати цю умову біля формули так: “| n → ∞” .

Трохи повозимся. Побудуємо кілька перетворень
(вважаючи їх тотожними).
Спочатку розіб'єм n на 𝓲 x∗n/(𝓲 x) аналогічно випадку вище. Підставимо це замість n у показнику, і перепишемо:

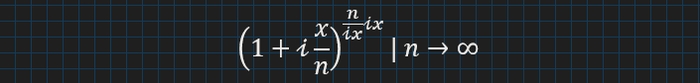
Знову можем розписати добуток показників і запхаєм 𝓲 в дужках до чисельника для зручності:

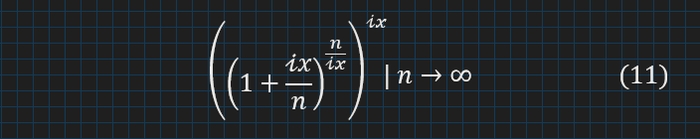
Тут зробим паузу.
n − Залишився великим, тому й дріб  n/(𝓲 x)  мав би бути великим, ну ніби-то. І можна перейти до параметру: t = n/(𝓲x) , він буде рости в нескінченність, якщо n  — теж. А от (𝓲 x)/n згідно нашій ідеї має бути малим, а ще (𝓲 x)/n = 1/t .
Маємо спрощений вигляд формули (11):

Згадаєм, що вираз (12) рівний εˣ . Для кращого вигляду розкладемо всі добутки в показниках степеня на послідовні піднесення до степеня:

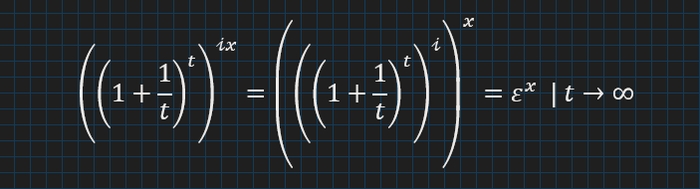
Нарешті ми одержали дещо кращу формулу, а ні ж просто ε¹ . Тепер ми бачимо, що

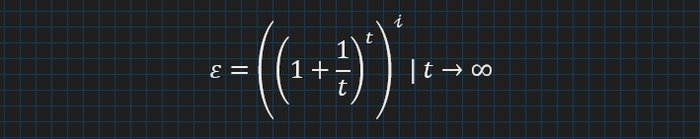
𝓲 - Константа, тому основне питання у внутрішніх дужках.

Границя

є як раз Другою чудовою границею, її значення позначають як  e .
e ≈ 2,7182818284590452353602874713527… — напрочуд “звичайне” число з нескінченним неперіодичним дробом, як π.
Однак, ми можемо навіть його не обчислювати, думаючи, що це якесь число і позначити першою буквою свого імені, на приклад е .

Отже, ми знайшли ε — саме те, що шукали, ε = eⁱ !

Підставимо це у (9) і маємо фінальну форму шуканої тотожності (3) :

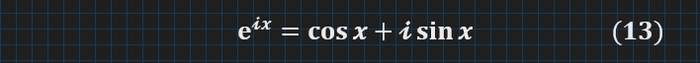
відома нині як формула Ейлера(Ойлера).

Критика

Хтось скаже

Ну нічого собі! Треба було Так возитися, щоб ввести поняття уявної одиниці ?!
Це ж такий самий класичний спосіб введеня компл‵ексних чисел!

— Ну дивіться, тут вже потрібно звернути увагу, що якась інша аналогія між експонентою (eˣ ) і тригонометричними функціями привела до того ж, до чого привела необхідність виводити √(-1) через чисто алгебраїчні причини (вирішування кубічних рівнянь, а разом з тим і квадратних).

Чесно кажучи, я не знаю, як Ейлер(Ойлер) її вивів… Я звик виводити на основі рядів(Тейлора): розкласти sin(x) потім cos(x), накінець для експоненти eⁱˣ (показникової функції), а потім констатувати факт, що сума рядів синуса і косинуса з тими множниками(B = 1, A = 𝓲 ) таки дорівнює ряду для експоненти від 𝓲x.

Тепер ми одержали зовсім іншим способом, але мабуть дійсно, історично, колись вже хтось так її виводив, навіть сам Ейлер(Ойлер), цього я не знаю.

Висновки

І ось, в цьому експромті проглядається оця, цікава особливість, що

зовсім на пустому місці, на якійсь туманній думці про зв’язок між тригонометричними і показниковими функціями( що є якась мультиплікативність)
— зразу вдалося одержати компл‵ексні числа.
А за одно й цікаву формулу з уявною одиницею 𝓲 !

Робили ми це місцями нечесно, але це не означає, що ми помилялися.

Серед читачів точно будуть ті, хто буде чіплятися за достовірність: “викладки погані!” , “засади слабкі!” , “аргументи нікудишні!” ,
“уявні числа типу n/(𝓲 x) — не порівнюються!!!”
Такі позиції теж бувають не зовсім правильні, бо можна некоректними способами щось одержати, а потім виправити і добре довести.

Тут проявляється сам дух такої, ранньої науки.
Науки тих часів, коли яму ще не так глибоко розкопали, що неочікувані цікаві відкриття можна було одержати просто на пустому місці, за декілька хвилин.

Бібліографія і кілька слів

Мені завжди було недостатньо мотивації введення тих чи інших математичних понять. Часто читаю різні блоги, і не всі автори стараються не просто розповісти “Як користуватись?”, а
“чому ми це вводимо? Чому саме так?” І очевидно, так може бути важче і довше.
І виходить : кількість і час проти якості і повноти.

Я вдячний Павлу Шестопалову за крутий контент. Це старий матеріал, який заслуговує уваги.

Основне джерело: https://www.youtube.com/watch?v=bKZVmO44SnQ

Він дуже крутий викладач і вчитель математики, має ще класні ідеї,
але він росіянин. І знання в соціальних науках у нього бажали би бути краще.
Ми з ним мали розмову у зв’язку з війною. Я так і не зрозумів його позицію. Він випустив декілька роликів, де висловив свої думки. Але це виглядало як сумніви у всіх і до всіх.
Можливо, винен його світогляд на основі філософії Рене Декарта
— історично відомого філософа, бо в нього є плейлист
“Скучающий Декарт”. От я так і думаю.
А в Декарта радикальний сумнів був основою суджень.

Я повинен був розповісти, бо хтось і справді міг піти за посиланням і глянути ці ролики. І це могло вельми зачепити чиїсь почуття.

Пропоную цінувати людей за щось хороше.

Дякую за увагу , і

Слава Україні !