
Апроксимація
Апроксима́ція — наближене вираження будь-яких величин (або геометричних/математичних об'єктів) через інші, більш відомі (близькі за значенням) або більш прості величини.
Якщо здається трішки складним, то це через те, що цей термін абстрактний і в нього можна запхати дуже багато математичних методів. Апроксимація це буквально - наближення.
Коли у вас є певний набір даних і ви хочете побачити закономірність між цими даними, наприклад функцію, яка їх описує, то саме для цього і використовується апроксимація. У нас є експериментальні дані і ми хочемо знайти функцію, яка їх породила, або описати її.
Інтерполяція і екстраполяція є методами апроксимації.
Інтерполяція
Інтерполяція — в обчислювальній математиці спосіб знаходження проміжних значень величини за наявним дискретним набором відомих значень.
Інтерполяція для множини x = [1, 3] буде [1, 2, 3]. Між 1 і 3 шукається середнє значення.
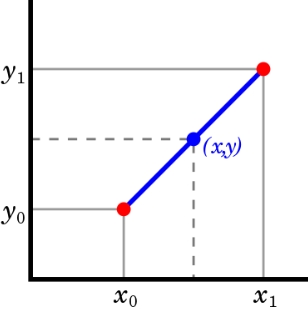
Інтерполяція по своїй природі є апроксимацією, адже вона дозволяє відтворити функцію на основі певних даних, а вирізняєї її від інших апроксимацій те, що результуюча функція повинна проходити через точки, які інтерполюються, тобто в інтерполяції ми шукаємо значення всередині.
Інтерполяція не завжди лінійна, вона може бути кубічною, або сферично лінійною.
Екстраполяція
Екстраполяція - це статистичний та математичний метод, який використовується для передбачення значень за межами вже відомого діапазону даних. У сутності, це означає застосування вже відомих даних або залежностей для розрахунку значень за межами цих даних.
Зрозуміло, що екстраполяція протилежна за значенням до інтерполяції, якщо в інтерполяції ми шукаємо значення всередині отриманих даних, то в екстраполяції ми хочемо знайти значення за межами відомого діапазону.
Зверніть увагу на префікс обох слів, інтер (між) та екстра (назовні/поза межами)
Загалом будь-який математичний метод суть якого полягає в передбаченні майбутніх даних можна назвати екстраполяцією.
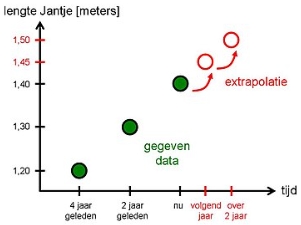
Екстраполяція також буває не тільки лінійною. Вона може бути: поліноміальною, експоненційною і так дальше.
Прикалад на Python
import numpy as np
from scipy import interpolate
import matplotlib.pyplot as plt
np.random.seed(0)
x = np.linspace(0, 10, 20)
y = np.sin(x) + np.random.normal(0, 0.2, 20)
f_linear = interpolate.interp1d(x, y, kind='linear')
f_cubic = interpolate.interp1d(x, y, kind='cubic')
f_extrap = interpolate.interp1d(x, y, kind='linear', fill_value='extrapolate')
x_interp = np.linspace(0, 10, 100)
y_linear_interp = f_linear(x_interp)
y_cubic_interp = f_cubic(x_interp)
x_extrap = np.linspace(-2, 12, 100)
y_extrap = f_extrap(x_extrap)
plt.figure(figsize=(12, 8))
plt.plot(x, y, 'o', label='Випадкові дані')
plt.plot(x_interp, y_linear_interp, '-', label='Лінійна інтерполяція', color='blue')
plt.plot(x_interp, y_cubic_interp, '--', label='Кубічна інтерполяція', color='green')
plt.plot(x_extrap, y_extrap, '-.', label='Екстраполяція', color='red')
plt.legend()
plt.title('Інтерполяція та Екстраполяція випадкових даних')
plt.xlabel('x')
plt.ylabel('y')
plt.grid(True)
plt.show()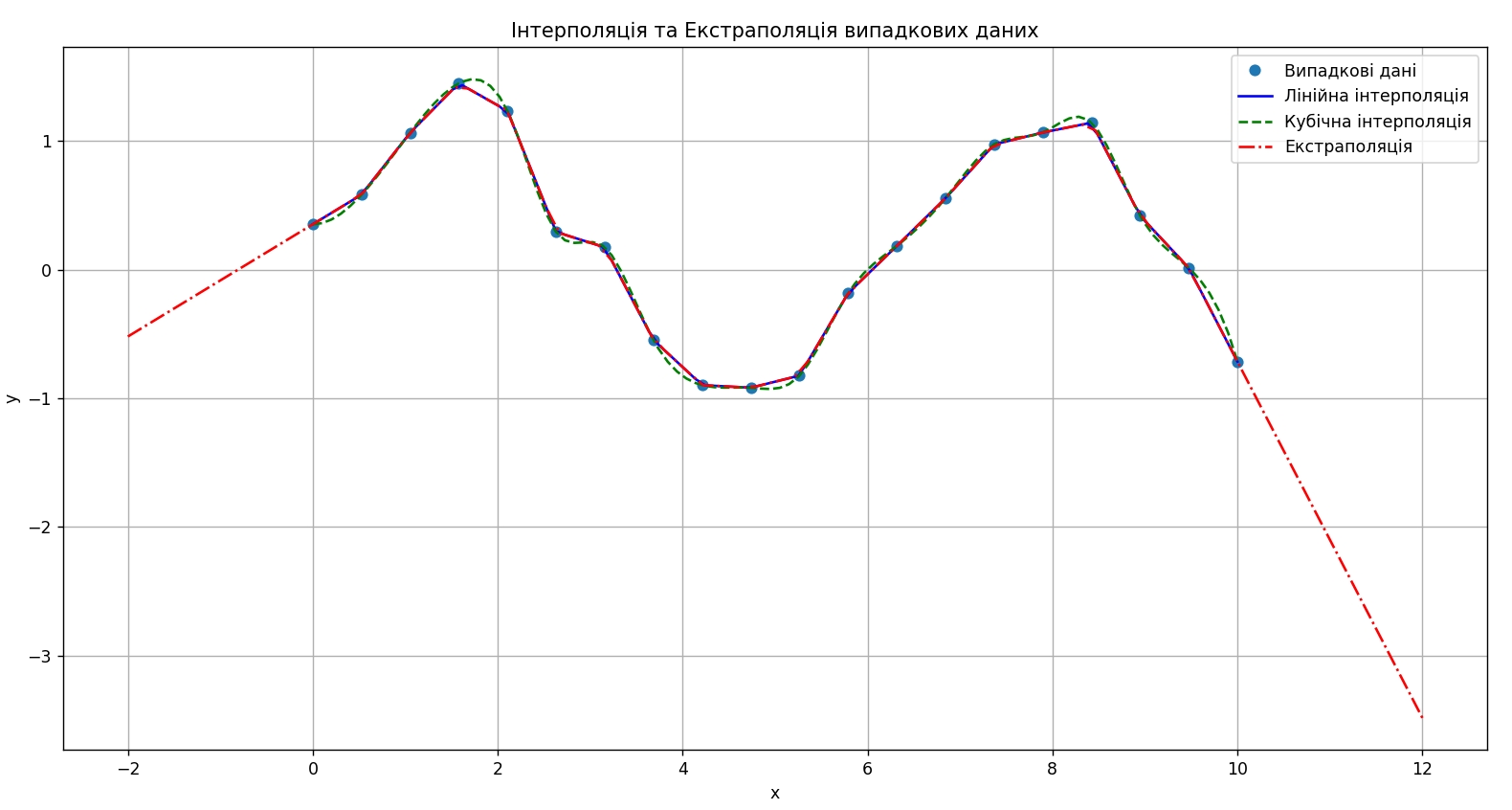
У цьому прикладі використовується лінійна та кубічна інтерполяція та екстраполяція випадково згенерованих даних на базі синусоїди з шумом.
y = np.sin(x) + np.random.normal(0, 0.2, 20)Екстраполяція проходить по діапазону всієї оригінальної функції і також розширює його новими даними. Діапазон екстраполяції [-2; 12], хоч оригінальна функція [0, 10], тобто діапазон даних для інтерполяції входить в діапазон даних для екстраполяції.
Це змушує нас подивитись на природу використання цих термінів, обидва підходи можуть використовувати однакову функцію для визначення нових даних, але інтерполяція обмежує себе діапазоном оригінальної функції, а екстраполяція бере діапазон оригінальної функції та ще й його розширює.
Ось прикладний спосіб використання апроксимації. Тут прогнозується зміна температури, використовуючи метод поліноміальної регресії на основі історичних даних.
Я вважаю надлишковим тут розглядати ще й методи регресії, тому виділю колись на це окремий пост.
import numpy as np
import matplotlib.pyplot as plt
from sklearn.preprocessing import PolynomialFeatures
from sklearn.linear_model import LinearRegression
from sklearn.pipeline import make_pipeline
days = np.array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
temperatures = np.array([20, 22, 21, 25, 30, 32, 36, 33, 31, 28])
days = days.reshape(-1, 1)
degree = 2
model = make_pipeline(PolynomialFeatures(degree), LinearRegression())
model.fit(days, temperatures)
next_day = np.array([[10]])
predicted_temperature = model.predict(next_day)
plt.scatter(days, temperatures, color='blue', label='Первинні дані')
plt.plot(days, model.predict(days), color='red', label=f'Поліноміальна регресія')
plt.scatter(next_day, predicted_temperature, color='green', marker='*', s=200, label='Передбачення на десятий день')
plt.xlabel('Дні')
plt.ylabel('Температура (°C)')
plt.title('Поліноміальна регресія для передбачення температури')
plt.legend()
plt.grid(True)
plt.show()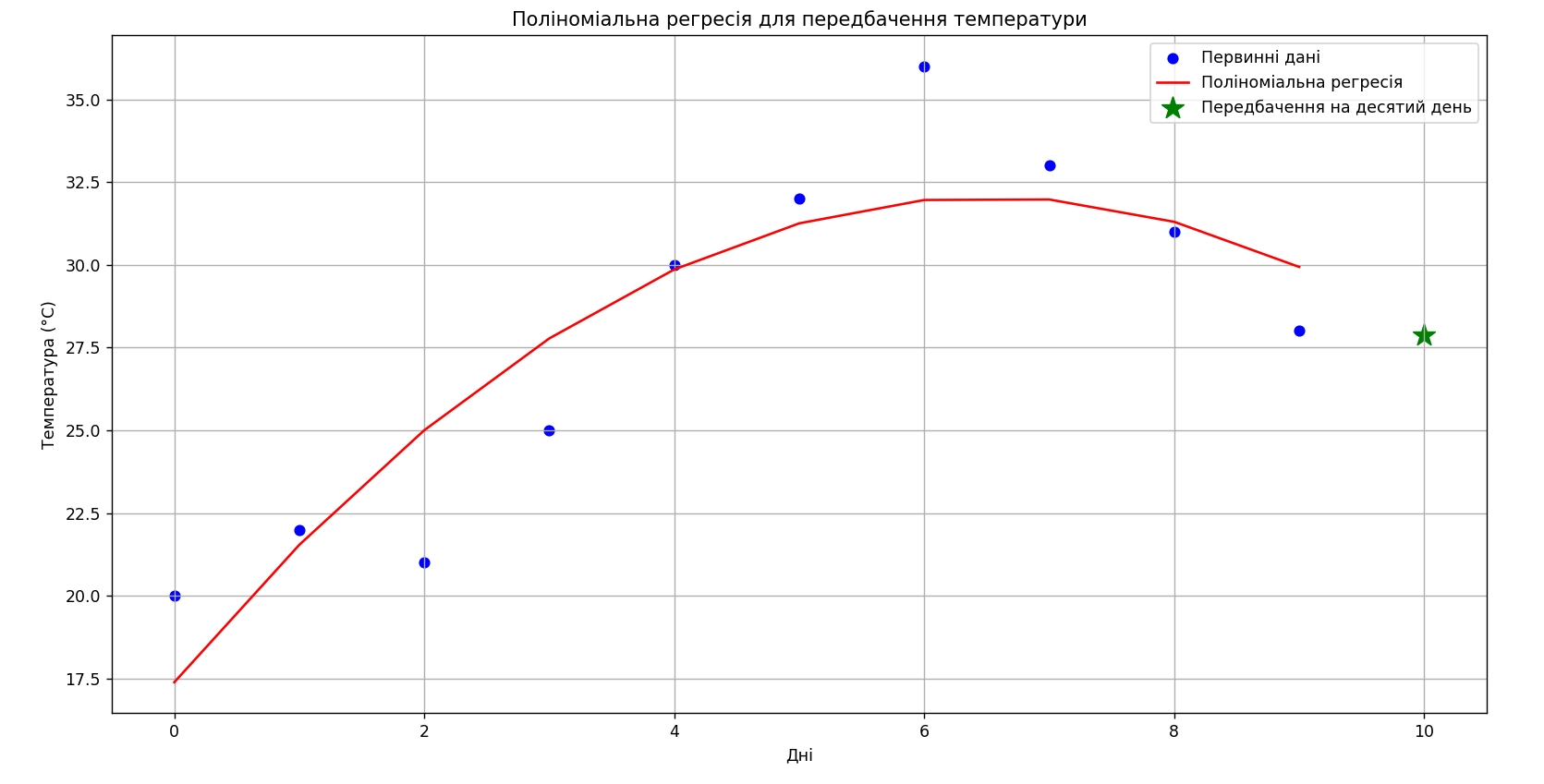
На прогнозування даних сильно впливає кількість історичної інформації та метод, який використовується. Важливо вміти підібрати правильний метод.
Для чого використовувати апроксимацію?
У багатьох випадках реальні процеси та фізичні явища можуть бути дуже складними для моделювання або розуміння. Апроксимація дозволяє створювати спрощені моделі для наближення цих процесів, що робить їх більш зрозумілими та керованими. Приємно бачити, коли все іде так, як ви цього очукуєте.
Апроксимація може бути використана для передбачення майбутніх значень на основі вже відомих даних. Це корисно у фінансах, економіці, метеорології та інших галузях, де важливо робити прогнози, наприклад гемблери люблять робити прогнози на футбольні матчі.
Також вона може використовуватися для створення математичних моделей, які можна використовувати для симуляції та вивчення складних систем.
